道路千万条

Posted 2022-02-23 xiaoyezi-wink

T83311 【音乐会】道路千万条

 

 

题解

 理解题面

也就是要给这n-1个运算符安排顺序，统计ans为true的方案数 t ，统计ans为false的方案数 f ,

求 t / ( t+f ) (mod 998244535 )

 

 思路

考虑最后算那种运算符，那么就有n-1种选择

（1）最后算 & ：ans为true：左项和右项同时为true

                           ans为false：左true右false，左false右true，左false右false

（2）最后算  | ：ans为true：左项和右项同时为true，左true右false，左false右true

                           ans为false：左false右false   

（3）最后算  ^：ans为true：左右不同，左true右false，左false右true

                           ans为false：左右相同，左true右true，左false右false

 

应用乘法分步原理和加法原理统计

 

SOLVE

 

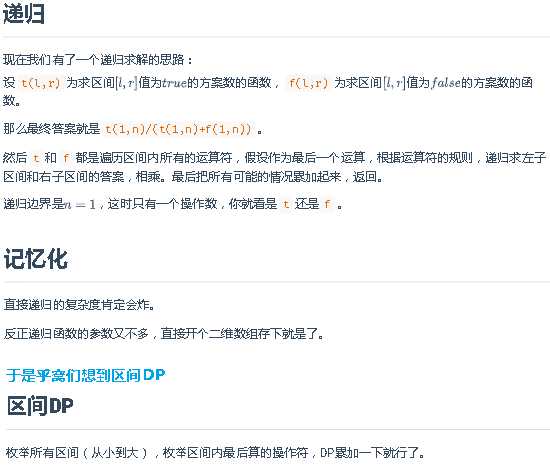
 注意

最后面除法转换成乘法逆元了

 

 

代码

#include<bits/stdc++.h>

using namespace std;

const int mod=998244353;
int n;
long long ans;
char s[505],opr[505];
//s存操作状态（t或f），opr存操作符（&，|，^） 
long long t[505][505],f[505][505];
//t存值为true的方案数，f存值为false的方案数 

inline int read1()    

    int ans=0;
    char last=‘ ‘,ch=getchar();
    while(ch<‘0‘||ch>‘9‘) last=ch,ch=getchar();
    while(ch>=‘0‘&&ch<=‘9‘) ans=ans*10+ch-‘0‘,ch=getchar();
    if(last==‘-‘) ans=-ans;
    return ans;
 

inline char read2()

    char c;
    do
    
        c=getchar();
    while(c==‘ ‘||c==‘\\n‘||c==‘\\0‘||c==‘\\t‘||c==‘\\r‘);


pair<long long,long long> extgcd(long long a,long long b)  //拓展欧几里得求逆元 

    if(b==0) 
    
        return make_pair<long long,long long>(1,0); 
    
    pair<long long,long long>ans=extgcd(b,a%b);
    ans.first^=ans.second^=ans.first^=ans.second;
    ans.second-=a/b*ans.first;
    return ans;


int main()

    n=read1();
    for(int i=1;i<n;i++)
    
        s[i]=read2();
        opr[i]=read2();
    
    s[n]=read2();
   
    for(int i=1;i<=n;i++)   //长度为1直接判断 
    
        if(s[i]==‘t‘) 
          t[i][i]=1,f[i][i]=0;
        else
          t[i][i]=0,f[i][i]=1;
    
    
    for(int len=2;len<=n;len++)  //枚举区间长 
      for(int i=1;i+len-1<=n;i++)  //区间起始位置 
      
          int j=i+len-1;  //区间结束位置 
          for(int k=i;k<j;k++)  //枚举最后算的运算符 ，注意这里 ，从i枚举到j-1
          
              if(opr[k]==‘&‘)
              
                  t[i][j]=(t[i][j]%mod+t[i][k]*t[k+1][j]%mod)%mod;
                  f[i][j]=(f[i][j]%mod+(f[i][k]*f[k+1][j])%mod+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod)%mod;
            
              if(opr[k]==‘|‘)
              
                  f[i][j]=(f[i][j]%mod+(f[i][k]*f[k+1][j])%mod)%mod;
                  t[i][j]=(t[i][j]%mod+(t[i][k]*t[k+1][j])%mod+(t[i][k]*f[k+1][j])%mod+(f[i][k]*t[k+1][j])%mod)%mod;
            
              if(opr[k]==‘^‘)  //注意这里（一开始记反了QWQ） 
              
                  t[i][j]=(t[i][j]%mod+(t[i][k]*f[k+1][j])%mod+f[i][k]*t[k+1][j]%mod)%mod;
                  f[i][j]=(f[i][j]%mod+t[i][k]*t[k+1][j]%mod+f[i][k]*f[k+1][j]%mod)%mod;
                
        
      
    
    ans=(t[1][n]*((extgcd(t[1][n]+f[1][n]%mod,mod).first%mod+mod)%mod))%mod;
    printf("%ld\\n",ans);
    
    return 0;