几个重要的分段函数

Posted 2022-02-22 shiliye

绝对值函数
　　$y=\\left|x\\right|=
　　\\left\\\\beginmatrix
　　x, x \\ge 0 &\\\\
　　-x, x < 0 &
　　\\endmatrix\\right.$

　　性质：

　　　　$\\left|x\\right|=x \\Leftrightarrow x \\ge 0，\\left|x\\right|=-x \\Leftrightarrow x \\le 0$

　　图形：

　　         

 

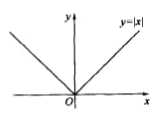
取整函数
　　$y=[x]=$小于或等于$x$的最大整数
　　用分段函数表示：$y=[x]=n,n \\le x <n+1$($n$是整数)

　　性质：

　　　　$[x] \\le x < [x] + 1,[x] = x \\Leftrightarrow x$是整数，$[x+y] \\ge [x]+[y],[x+n]=[x]+n$($n$是整数)

　　图形：(阶梯曲线)

　          　

 

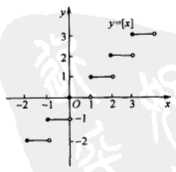
符号函数
　　$y=sgnx=
　　\\left\\\\beginmatrix
　　1,& x > 0 \\\\
　　0,& x = 0 \\\\
　　-1,& x < 0
　　\\endmatrix\\right.$

　　性质：
　　　　$sgnx=1 \\Leftrightarrow x > 0, sgnx=-1 \\Leftrightarrow x < 0$
　　　　$sgn(x-a) = 1 \\Leftrightarrow x > a, sgn(x-a) = -1 \\Leftrightarrow x < a$
　　　　$x=sgnx \\cdot \\left|x\\right|,\\left|x\\right|=sgnx \\cdot x$

　　图形：

　　　　

 

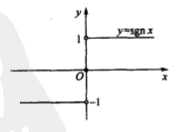
狄利克雷函数
　　$y=D(x)=
　　\\left\\\\beginmatrix
　　1,& x是有理数 \\\\
　　0,& x是无理数
　　\\endmatrix\\right.$

　　性质：
　　　　狄利克雷函数有很多糟糕的性质
　　　　1) 狄利克雷函数没有图形(没有任何曲线段)
　　　　2) 狄利克雷函数是以任何正有理数为周期的周期函数，因此它没有最小的正周期
　　　　3) 狄利克雷函数处处无极限，处处不连续，处处不可导，在任何区间上不可积
　　　　狄利克雷函数常用来举反例和构造具有某种特殊性质的函数
　　　　如函数:$y=xD(x)$仅在原点连续，在其他点处间断，
　　　　函数$y=x^2D(x)$仅在原点可导，在其他点处间断(从而不可导)

　　注意：

　　　　狄利克雷函数可以用极限定义为$D(x)=\\lim_m \\rightarrow \\infty [\\lim_n \\rightarrow \\infty cos^n(\\pi m!x)]$