算法--时间和空间复杂度

Posted 2022-02-21 pankypan

算法(1)--时间和空间复杂度

初识

算法定义

算法是独立存在的一种解决问题的方法和思想：

• 求解一个问题步骤的描述
• 是求解问题的方法
• 它是指令的有限序列
• 其中每条指令表示一个或者多个操作

对于算法而言，实现的语言并不重要，重要的是思想

算法特性

• 确定性：无二义
• 有穷性：合适时间内可以执行
• 输入项
• 输出项
• 可行性：算法的每一步都是可行的

复杂度

时间复杂度

定义

? 一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示（语句频度），若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))，称O(f(n))为算法的渐进时间复杂度(O是数量级的符号 )，简称时间复杂度。

求解步骤

求解算法时间复杂度的步骤：

1. 找出算法中的基本语句，计算基本操作执行次数T(n)

   # 基本操作即算法中的每条语句（以;号作为分割），语句的执行次数也叫做语句的频度。在做算法分析时，一般默认为考虑最坏的情况。

2. 计算基本语句的执行次数T(n)的数量级

    # 忽略常量、低次幂和最高次幂的系数，令f(n)=T(n)的数量级

3. 用大O来表示时间复杂度

   # 当n趋近于无穷大时，如果lim(T(n)/f(n))的值为不等于0的常数，则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n))，即为时间复杂度。

example_1:

n = 1000  # T(n) = 1
j = 1   # T(n) = 1
num1 = 1   # T(n) = 1
num2 = 2   # T(n) = 1
for i in range(0, n):   # T(n) = n
    num1 += 1   # T(n) = n
    while j < n:  # T(n) = n*log(n), 以2为底
        j *= 2  # T(n) = n*log(n), 以2为底
        num2 += 1  # T(n) = n*log(n), 以2为底
print(num1, num2)  # T(n) = 1

1. 总的T(n):
   \\[ T(n) = 5 + 2n + 3nlog_2n \\]

2. 忽略掉T(n)中的常量、低次幂和最高次幂的系数，数量级
   \\[ f(n) = nlog_2n \\]

3. 求极限
   \\[ lim(T(n)/f(n)) = lim((3nlog_2n + 2n + 4)/(nlog_2n) = 3 \\]
   所以时间复杂度可以用大O表示，为
   \\[ O(f(n)) = O(nlog_2n) \\]

简化的计算步骤：

可以看出，决定算法复杂度的是执行次数最多的语句，这里是num2 += 1，j *= 2一般也是最内循环的语句。并且，通常将求解极限是否为常量也省略掉？

1. 找到执行次数最多的语句
2. 计算语句执行次数的数量级
3. 用大O来表示时间复杂度

example_1

# 1.执行次数最多的语句为
while  j < n:
    j *= 2
    num2 += 1
T(n) = 3n*log(n) 

# 2.数量级
f(n) = n*log(n)

# 3.求极限及大O表示
T(n) = O(nlog(n))

几种可能

分析算法，存在的几种可能：

• 平均时间复杂度
• 最坏时间复杂度
• 最优时间复杂度

一些规则

• 基本操作，即只有常数项，认为是O(1)

• 顺序结构，时间复杂度按加法进行计算
  \\[ T(n, m) = T1(n) + T2(m) = O(max(f(n), g(m))) \\]

• 循环结构，时间复杂度按乘法进行计算
  \\[ T(n, m) = T1(n) * T2(m) = O(f(n)*g(m)) \\]

• 分支结构，时间复杂度取最大值

常见的时间复杂度算法：

执行次函数举例--总的T(n)	时间复杂度	非正式术语
12	O(1)	常数阶
2n + 3	O(n)	线性阶
3n^2 + 2n + 1	O(n^2)	平方阶
5log(n) + 20	O(log(n))	对数阶
2n + 3nlog(n) + 19	O(nlog(n))	nlog(n)阶
6n^3 + 2n^2 + 3n + 4	O(n^3)	立方阶
2^n	O(2^n)	指数阶
n! + nlog(n) + 15	O(n!)	阶乘

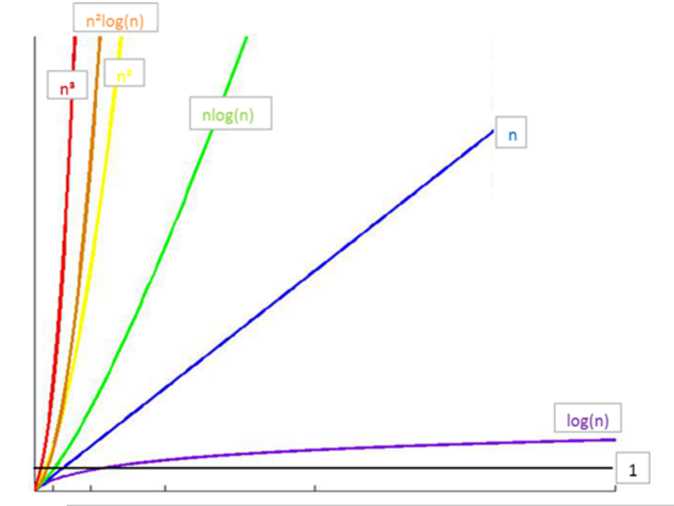
所消耗的时间从小到大：
\\[ O(1) < O(log(n)) < O(n) < O(nlog_2(n)) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n) \\]

示例演练

example_2

n = 1000
x = 1

for i in range(0, n):
    x += 1  # T(n) = n

for i in range(0, n):
    for j in range(0, n):
        x += 1  # T(n) = n*n
print(x)

分析：注意：T(n)为执行次数最多语句的频度

• 第一个for loop, T(n) = n; f(n) = n时间复杂度为O(n)
• 第二个for loop, T(n) = n^2; f(n) = n^2,时间复杂度为O(n^2)
• 整个算法的时间复杂度为O(n + n^2) = O(n^2)

---

example_3

def func(n):
    for i in range(n):
        for j in range(i, n):
            print("Hello World j = %s" % j)  # T(n) = (n^2)/2 + n/2

分析：注意：==T(n)为执行次数最多语句的频度

• 直接找到语句频度最高的语句为print("Hello World j = %s" % j),

  # 当i为0时，该语句执行n次
  # 当i为1时，该语句执行n-1次
  # 。。。
  # 所以该语句的T(n) = n + (n-1) + (n-2) + ... + 1 = (n+1)*n/2 = 0.5n^2 + 0.5n

• 数量级f(n) = n^2

• 极限存在，时间复杂度 = O(n^2)

---

example_4

def func(n):
    if n <= 1:
        return 1
    else:
        return func(n - 1) + func(n - 2)

分析：

显然运行次数，T(0) = T(1) = 1，同时 T(n) = T(n - 1) + T(n - 2) + 1，这里的 1 是其中的加法算一次执行。
显然 T(n) = T(n - 1) + T(n - 2) 是一个斐波那契数列，通过归纳证明法可以证明，当 n >= 1 时 T(n) < (5/3)^n，同时当 n > 4 时 T(n) >= (3/2)^n。
所以该方法的时间复杂度可以表示为 O((5/3)^n)，简化后为 O(2^n)。

空间复杂度

类似于时间复杂度的讨论，一个算法的空间复杂度(Space Complexity)，S(n)定义为该算法所耗费的存储空间，它也是问题规模n的函数。渐近空间复杂度也常常简称为空间复杂度。
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。一个算法在计算机存储器上所占用的存储空间，包括:

• 存储算法本身所占用的存储空间
  • 存储算法本身所占用的存储空间与算法书写的长短成正比，要压缩这方面的存储空间，就必须编写出较短的算法
• 算法的输入输出数据所占用的存储空间
  • 算法的输入输出数据所占用的存储空间是由要解决的问题决定的，是通过参数表由调用函数传递而来的，它不随本算法的不同而改变
• 算法在运行过程中临时占用的存储空间
  • 算法在运行过程中临时占用的存储空间随算法的不同而异，有的算法只需要占用少量的临时工作单元，而且不随问题规模的大小而改变，我们称这种算法是“就地"进行的，是节省存储的算法；有的算法需要占用的临时工作单元数与解决问题的规模n有关，它随着n的增大而增大，当n较大时，将占用较多的存储单元，例如快速排序和归并排序算法就属于这种情况

---

常见算法空间复杂度：

• 一个算法的空间复杂度为一个常量，即不随被处理数据量n的大小而改变时，可表示为O(1)；
• 当一个算法的空间复杂度与以2为底的n的对数成正比时，可表示为0(1og2n)；
• 当一个算法的空I司复杂度与n成线性比例关系时，可表示为0(n).若形参为数组，则只需要为它分配一个存储由实参传送来的一个地址指针的空间，即一个机器字长空间；若形参为引用方式，则也只需要为其分配存储一个地址的空间，用它来存储对应实参变量的地址，以便由系统自动引用实参变量。