集成学习-Adaboost 进阶

Posted 2022-02-13 yanshw

adaboost 的思想很简单，算法流程也很简单，但它背后有完整的理论支撑，也有很多扩展。

 

权重更新

在算法描述中，权重如是更新

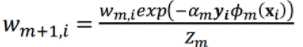
其中 w_m,i 是m轮样本i的权重，α_m是错误率，Ø_m是第m个基学习器的输出，Zm是归一化因子

 

当预测值与真实值相同时，yØ=1，-αyØ<0，exp(-αyØ)<1，权重降低；

当预测值与真实值不同时，yØ=-1，-αyØ>0，exp(-αyØ)>1，权重增加；

而且变化幅度由α确定；

 

这样可以说得通，但是这个式子是怎么来的呢？

原理推导

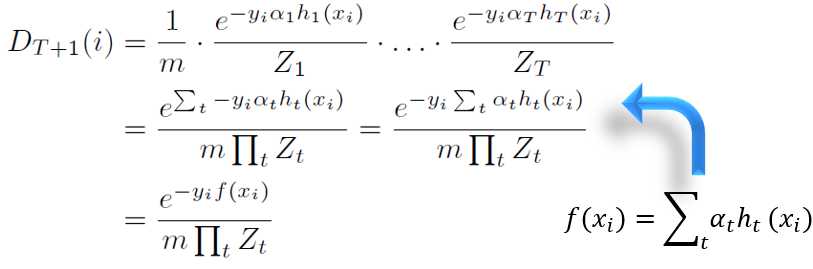
第一个式子表示权重的连乘，每个乘子是第t轮的权重，前T个乘子就是 D_T，用D_T乘以最后一项就是最开始的式子。

 

f(x)是组合分类器的输出，y_i是个常数，所以上式如是变形。

这里要注意，h(x)是基分类器的输出，其值域为-1,1，而f(x)是组合分类器的输出，其值域不是-1,1

 

错误上界

Abdboost 一个很重要的特性就是拥有错误上界，而且随着迭代的增加，上界逐渐降低。

 

首先

这里的 H(x) 是 adaboost 最后的输出，f(x)为组合分类器的输出，H(x)=sign(f(x))，很容易推出 yf(x)≤0

[H(x)≠y] 表示当 [ ] 内成立时，值为1，否则为0，显然

m为样本个数

显然不等号左边就是错误率

 

由【权重更新】的公式可得

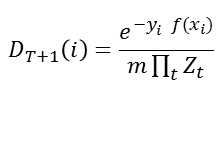
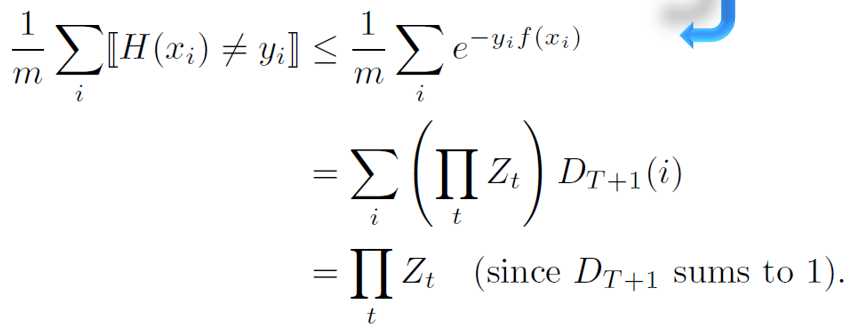
D是归一化的，ΣD和为1

 

错误上界就是 ∏Z

感性理解：Z是权重 x 损失，基分类器越好，Z越小，基分类器越多，ΠZ越小

 

损失函数

错误率存在上界ΠZ，其实就是损失函数

 

指数损失函数

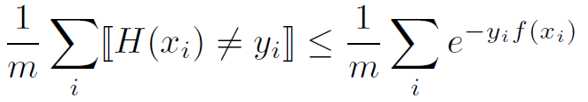
实际上Adaboost的损失函数为指数损失函数

指数损失函数有个特性：分错时，损失很大，分对时，损失很小，指数级增加，这使得减小损失的重点放在分错的样本上。

这就是 Adaboost 的思想。

 

到这你可能认为这个指数损失来的蹊跷，明明是ΠZ啊，确实如此，Adaboost作者的说法是，指数损失函数并不是算法设计的初衷，但是它更好的解释了算法，并提供了扩展空间。

 

为什么是加性模型

最终的损失函数为 ΠZ

这个损失函数是连乘，且乘子之间存在串行关系，这很难通过梯度下降等方法获取最优解。

采用贪心策略，保证每个Z最小，那就认为 ΠZ 最小。

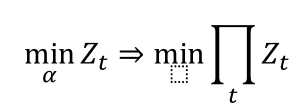
这就是 Adaboost 为什么是加性模型。

 

梯度下降 

每一步最小化损失 Z

 

先对 exp(-αyh(x)) 实施一个很常用的变形

当 y=h(x) 时，exp(-αyh(x))=exp(-α)

当 y≠h(x) 时，exp(-αyh(x))=exp(α)

只能取两个值

那么 exp(-αyh(x)) 到底等于 exp(-α) 还是 exp(α)，或者说以一定概率等于 exp(-α) 和 exp(α) 

二分类，两个概率和为1

 

对Z进行梯度下降

Z对应了一个固定的分类器，预使Z最小，能改变的只有α，于是对α求导，令导数等于0

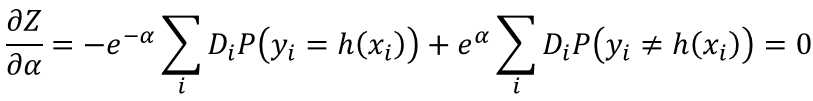
P(y≠h(x)) 即错误的概率，也就是错误率，用ε表示

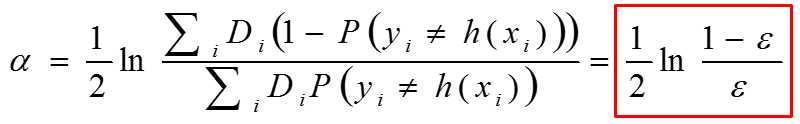
 α 就是加性模型的系数

也就是算法流程中基分类器的系数。

 

为什么错误率要小于0.5

有人说错误率大于0.5，还不如瞎猜，基分类器太渣，有一定道理

但从数学角度来考虑，当ε<0.5时，α<0，也就是说这个分类器只起到了反作用，请问你是来捣乱的吗？轰出去

处理方式有两种，一是直接结束迭代，二是放弃这个基分类器，重新训练一个，这种适合带随机的Adaboost。

 

此时再来看Adaboost的算法流程

每一步是不是很清楚。

 

多分类

原始的 Adaboost 是二分类模型，是因为最后的 sign 只能映射到2个类。

 

那能否实现多分类呢？当然可以，并且有多种方法

 

Adaboost.M1

纵观上面的原理推导，只有在对Z求导时，用到了二分类，即两个概率和为1，

但是对一个样本而言，它的预测值只有等和不等真实值两种情况，所以不管是多分类还是二分类，求导方法相同。

再来看看求导过程

 

 确实如上所说。

 

M1的思路和Adaboost完全相同，只是把基分类器由二分类器改成了多分类器，最后的sign函数肯定要换掉

其实就是统计哪个类被分的最多，只是计数时要乘以权重。

 

缺点：Adaboost 要求基分类器错误率小于0.5，这对二分类器来说很正常，但是对于多分类器过于严格。

 

Adaboost.SAMME

M1的改进版

与Adaboost算法流程相同，只是改变了分类器权重的计算

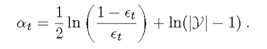
其他基本同M1，算法大致如下

 

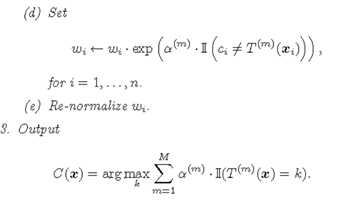
要使 α>0

此时 错误率 不是小于0.5，而是1-1/k，如0.8,0.9等，更为宽松，解决了M1的问题。

 

Adaboost.SAMME.R

该算法类似 Adaboost.SAMME，只是它使用的基分类器输出为概率。

具体请百度

 

Adaboost.MH

采用一对多的思想，见我的博客 二分类实现多分类

 

还有其他实现多分类的方法，不再赘述。

 

VS 随机森林

随机森林，每棵树是个强分类器，甚至过拟合，偏差很小，方差很大，模型目标主要是降低方差；

Adaboost，每棵树是个弱分类器，偏差很大，方差很小，模型目标主要是降低偏差。　　　　　　【偏差降低后，模型目的达到，就成了强分类器】

 

 

 

参考资料：

https://zhuanlan.zhihu.com/p/34842057

https://zhuanlan.zhihu.com/p/25096501

https://www.zhihu.com/search?type=content&q=adaboost%20%20mh