数据结构之差分数组

Posted 2022-02-11 aiahtwo

2019-06-25

推荐博客阅读：https://www.sohu.com/a/271430685_100201031

一. 适合解决的问题

有n个数。m次操作,每一次操作,给定l,r,del.将l~r区间的所有数增加del；最后有q个询问,给你 l,r ,每一次询问求出l~r的区间和。

注明： 先进行m个修改操作,后进行查询操作.

涉及到的用途有

• 快速处理区间加减操作：O(1)
• 询问区间和:O(n)处理O(1)查询.

 

二. 算法解释

差分数组定义：记录当前位置的数与上一位置的数的差值. 

我们发现差分数组的前缀和s[i]就是原数组a[i]的值

 

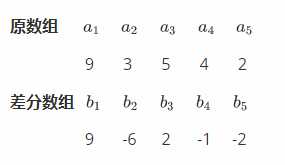
差分数组的前缀和：9  3  5  4   2

现在对原数组a进行区间操作：

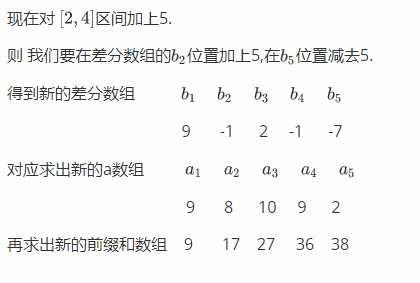
我们可以发现图中对新的差分数组进行前缀和的数组（即图中的新的a数组）和对原数组a进行区间操作后的数组a一模一样

另外，可以通过图中新的前缀和数组(假设为sum) 求出  区间操作后的数组a的区间和

beforesum(a~b)=sum[b]-sum[a-1];

 

三.关键代码

简化版：

解释版：

#include<iostream>
#include<string.h>
#include<cstring>
#include<cstdio>
using namespace std;
#define N 100005
int main()

    int a[N],b[N];
    int n;//数组a的长度
    cout<<"请输入数组a的长度："<<endl;
    cin>>n;
    cout<<"请输入数组a的元素："<<endl;
    for(int i=1;i<=n;i++)
        cin>>a[i];
        
    memset(b,0,sizeof(b));
    a[0]=0;//很重要
    for(int i=1;i<=n;i++)//差分数组就是原数组前后数的差值
        b[i]=a[i]-a[i-1];

    cout<<"差分数组："<<endl;
     for(int i=1;i<=n;i++)
        cout<<b[i]<<" ";
     cout<<endl<<endl;

    int m;//区间修改操作的组数
    cout<<"请输入需进行区间修改操作的组数："<<endl;
    cin>>m;
    while(m--)
    
        int l,r,x;//被区间修改的左边界与右边界  x为增加的值
        cout<<"请输入需进行区间修改操作的的左边界与右边界以及要增加的值："<<endl;
        cin>>l>>r>>x;
        b[l]+=x;
        b[r+1]-=x;
    

    cout<<"区间修改操作后的差分数组："<<endl;
     for(int i=1;i<=n;i++)
        cout<<b[i]<<" ";
     cout<<endl<<endl;

    int a1[N];
    memset(a1,0,sizeof(a1));
    for(int i=1;i<=N;i++)
        a1[i]+=a1[i-1]+b[i];

    cout<<"区间修改操作后的差分数组的前缀数组（也即原数组进行区间修改后的更改数组）："<<endl;
     for(int i=1;i<=n;i++)
        cout<<a1[i]<<" ";
     cout<<endl<<endl;

     int sum[N];
     memset(sum,0,sizeof(sum));
     for(int i=1;i<=N;i++)
        sum[i]=sum[i-1]+a1[i];

    cout<<"修改后的数组的区间和数组"<<endl;
     for(int i=1;i<=n;i++)
        cout<<sum[i]<<" ";
    cout<<endl<<endl;

    cout<<"请输入需进行区间和查询操作的组数："<<endl;
    int t;//区间和查询操作的组数
    cin>>t;
    while(t--)
        int l,r;
        cout<<"请输入需进行区间和查询操作的左右边界："<<endl;
        cin>>l>>r;
        cout<<"该查询区间的区间和："<<sum[r]-sum[l-1]<<endl;
    

样例一：
5
9 3 5 4 2
1
2 5 5
1
2 5
样例二：
5
9 3 5 4 2
1
2 4 5
1
2 4

四.例题

借教室：https://ac.nowcoder.com/acm/problem/16564

思路：该题对时间复杂度要求很高，一般的写法都会被卡

用线段树或者差分数组进行区间修改，每个区间修改操作都是O(1)

然后用二分找答案（求需求存在问题时申请人的编号）l=1,r=m

Judge()函数判断前mid个申请人是否会存在问题（前mid个申请人的需求是否不超过可供应值）

需求数组b（1~n）：前mid个申请人在第i天的总需求量

memset(b,0,sizeof(b));

for(int i=1;i<=mid;i++)//mid个申请人

for(int j=s[i];j<=t[i];j++)//s[i]到t[i]天每天的需求   区间修改

b[j]+=d[i];//第j天的需求为mid个申请人在该天的需求

这种写法绝对会超时间复杂度，所以我们采用差分数组来进行区间修改：

由于需求数组开始的值就全为0，它的差分数组也是为0，所以我们就省略求差分数组的那步，直接进行区间修改。

memset(b,0,sizeof(b));

for(int i=1;i<=mid;i++)//mid个申请人

b[s[i]]+=d[i];

b[t[i]+1]-=d[i];

 1 #include<iostream>
 2 #include<string.h>
 3 #include<cstring>
 4 #include<cstdio>
 5 using namespace std;
 6 //思路：二分+差分数组
 7 int n;
 8 int f[1000005],sum1[1000005],r[1000005],d[1000005],s[1000005],t[1000005];
 9 int Judge(int mid)
10     memset(f,0,sizeof(f));
11     for(int i=1;i<=mid;i++)//差分数组   多组区间修改
12         f[s[i]]+=d[i];
13         f[t[i]+1]-=d[i];
14     
15     sum1[0]=0;
16     for(int i=1;i<=n;i++)
17     
18         sum1[i]=sum1[i-1]+f[i];
19         if(sum1[i]>r[i])//说明需求比实际可供应大  申请存在问题
20         return 0;//说明小了
21     
22     return 1;
23  
24 int main()
25 
26     int m;
27     while(~scanf("%d%d",&n,&m))
28     
29         r[0]=0;
30         for(int i=1;i<=n;i++)
31         
32             scanf("%d",&r[i]);
33         
34         for(int j=1;j<=m;j++)
35         
36             scanf("%d%d%d",&d[j],&s[j],&t[j]);
37  
38         
39         if(Judge(m))
40             printf("0\\n");
41         else
42         int l=1,r=m,mid,ans=0;
43         while(l<=r)
44            mid=(l+r)/2;
45             if(Judge(mid)==0)//答案就是求需求存在问题时申请人的编号
46             
47                 r=mid-1;
48                 ans=mid;
49             
50             else
51                 l=mid+1;
52         
53         printf("-1\\n");
54         printf("%d\\n",ans);
55         
56     
57