量子逻辑门

Posted 2022-02-08 zmzzzz

量子态的演化

在前面量子纠缠1中我们已经提到了量子比特的线性代数表示，即，对于一个量子态 \\(\\alpha_0 | 0\\rangle +\\alpha_1 | 1\\rangle\\)我们可以化简成$ \\left[ \\beginarray\\alpha_0 \\ \\alpha_1\\endarray\\right]$ 。

量子态不是一成不变的，就像高电平会变成低电平，一个量子态也能演化成另一个量子态，量子态的演化就是在Hilbert空间中的旋转,如图(a)所示。

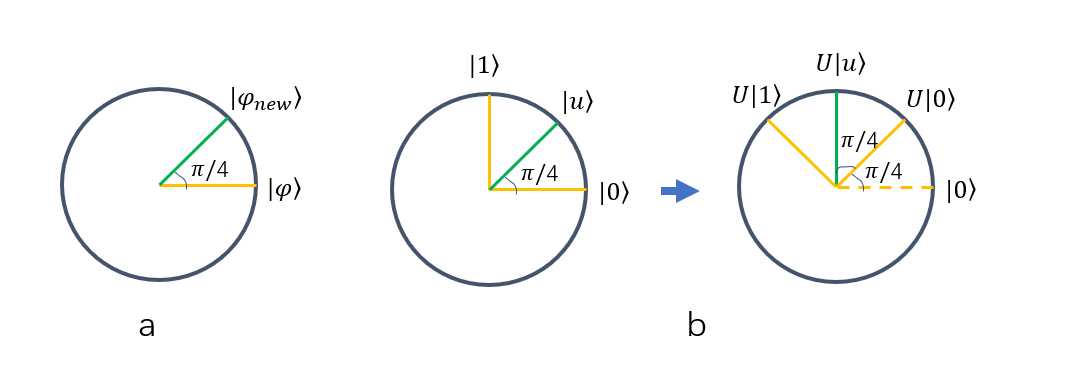
通过一个U操作，我们就将 \\(| 0\\rangle\\) 变成了 \\(U| 0\\rangle\\) ， \\(| 1\\rangle\\) 变成了 \\(U| 1\\rangle\\) ， \\(| u\\rangle\\) 变成了 \\(U| u\\rangle\\) ，如图(b)所示。需要注意的是，我添加一个U操作，没有改变 \\(| 0\\rangle\\) 、 \\(| 1\\rangle\\) 、 \\(| u\\rangle\\) 之间的关系， \\(U| 0\\rangle\\) 、 \\(U| 1\\rangle\\) 和 \\(| 0\\rangle\\) 、 \\(| 1\\rangle\\) 一样，他们之间的关系依旧是垂直。

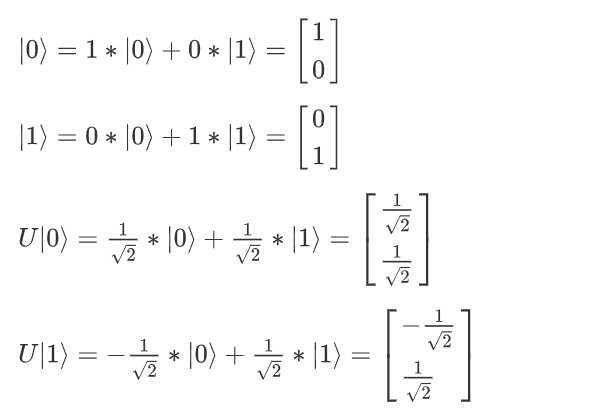
$ (| 0\\rangle, | 1\\rangle)=0$

$ (U| 0\\rangle, U| 1\\rangle)=0$

\\((,)\\) 是内积的意思， $ (| 0\\rangle, | 1\\rangle)= \\left[ \\beginarray1&0\\endarray\\right]\\left[ \\beginarray0 \\ 1\\endarray\\right]$ ，同样，也可以简写成 \\(\\langle0| 1\\rangle\\) ， \\(\\langle0|\\) 表明是 \\(| 0\\rangle\\) 的共轭转置。

对于这种两个向量之间夹角不会变的旋转称为刚性旋转 rigid rotation。

而这种U操作被成为酉操作，也是unitary transformation

Unitary Transformation

量子比特我们用向量来表示，因为我们量子比特的演化是线性的，所以在量子比特上的操作，可以用矩阵来表示。

单量子比特是 \\(2*1\\) 的向量，则单量子比特门是 \\(2*2\\) 的矩阵。

\\(| 0\\rangle\\) 变到 \\(U| 0\\rangle\\) 在线性代数上就是 $ \\left[ \\beginarray1 \\ 0\\endarray\\right]$ 变到 $ \\left[ \\beginarray\\frac1\\sqrt2 \\ \\frac1\\sqrt2\\endarray\\right]$

\\[ \\left[ \\beginarray\\frac1\\sqrt2 \\\\ \\frac1\\sqrt2\\endarray\\right]=U\\left[ \\beginarray1 \\\\ 0\\endarray\\right]\\]

\\[U= \\left[ \\beginarray\\frac1\\sqrt2 &-\\frac1\\sqrt2 \\\\ \\frac1\\sqrt2&\\frac1\\sqrt2 \\endarray\\right]\\]

对于旋转了 \\(\\theta\\) 角度的操作，都可以用 \\(U_\\theta= \\left[ \\beginarraycos\\theta &-sin\\theta \\\\ sin\\theta&cos\\theta \\endarray\\right]\\) 表达。

如果要做相反操作，就是将顺时针转 \\(\\theta\\) 角度， \\(U_-\\theta= \\left[ \\beginarraycos\\theta &sin\\theta \\\\ -sin\\theta&cos\\theta \\endarray\\right]\\)

很巧的是， \\(U_\\theta^\\dagger=U_-\\theta\\) ， \\(\\dagger\\) 是共轭转置的意思。

\\(U_\\theta U_\\theta^\\dagger=I\\) ，意思也很好理解，因为顺时针 \\(\\theta\\) 又 \\(-\\theta\\) ，正好就回到原位。

事实上所有的量子操作都是可逆的，所有的量子操作都酉操作。

那么什么是酉操作呢？

U is unitary iff \\(U^\\dagger U =I\\)

对于酉矩阵的更多特征会在线性代数的章节提到，这里主要提一个，酉矩阵是保内积的。

保内积又是什么意思？

两个向量在乘以相同的U后，他们的内积不变。

\\[(U| a\\rangle, U| b\\rangle)=\\langle a|U^\\dagger U|b\\rangle=\\langle a|I|b\\rangle=\\langle a|b\\rangle\\]

单量子逻辑门

量子逻辑门和经典逻辑门一个巨大的不同是——量子逻辑门可逆。

经过了经典的逻辑门与门或者非门，我们的信息会丢失，告诉你与门后的输出结果是0，你知道与门前的输入吗？（0，0）、（0，1）、（1，0）都有可能。

而对于量子逻辑门来说，我经过U变换后的结果是 \\(|a\\rangle\\) ，那么 \\(U^\\dagger |a\\rangle\\) 就是变换前的输入了。

举例几个常用的单量子逻辑门：

\\(X=\\left[ \\beginarray0 &1 \\\\ 1&0 \\endarray\\right]\\)，X门又称为比特翻转，他可以把 \\(|0\\rangle\\) 变成 \\(|1\\rangle\\) ，把 \\(|1\\rangle\\) 变成 \\(|0\\rangle\\) 。

\\(Y=\\left[ \\beginarray0 &-i \\\\ i&0 \\endarray\\right]\\)

\\(Z=\\left[ \\beginarray1 &0 \\\\ 0&-1 \\endarray\\right]\\)，Z门又称为相位翻转门，可以把 \\(|+\\rangle\\) 变成 \\(|-\\rangle\\) ， \\(-|1\\rangle\\) 变成 \\(|1\\rangle\\) 。

以及一个特别有用的门，Hadamard门：
\\(H=\\left[ \\beginarray\\frac1\\sqrt2 &\\frac1\\sqrt2 \\\\ \\frac1\\sqrt2&-\\frac1\\sqrt2 \\endarray\\right]\\) ，他的作用是把 \\(|1\\rangle\\) 变成 \\(|-\\rangle\\) ， \\(|0\\rangle\\) 变成 \\(|+\\rangle\\) 。

两量子逻辑门

对于两量子比特来说，他们的状态是 \\(\\alpha_00 | 00\\rangle+\\alpha_01 | 01\\rangle+\\alpha_10 | 10\\rangle+\\alpha_11 | 11\\rangle\\) ，需要用 \\(4*1\\) 的向量来描述，也就是 $ \\left[ \\beginarray\\alpha_00 \\ \\alpha_01 \\ \\alpha_10 \\ \\alpha_11 \\endarray \\right]$ ，对应操作两比特的逻辑门，也就是 \\(4*4\\) 的矩阵了。

两比特的量子门有各自管各自的，如图(c)，也有一个控制另一个的，如图(d)。

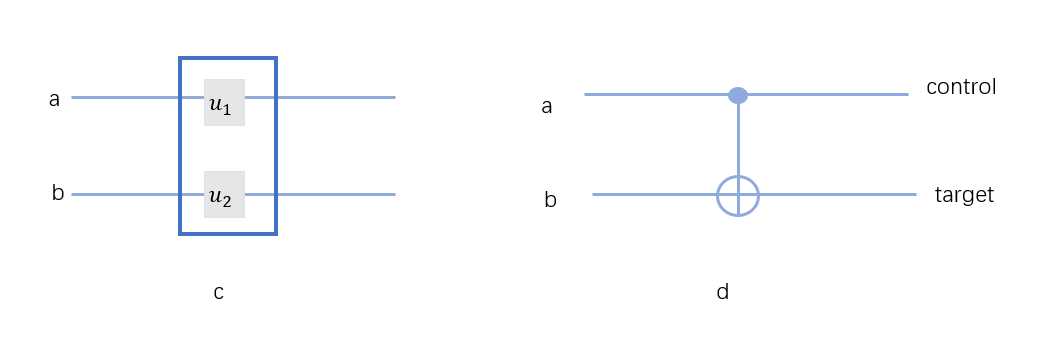
对于图c来说， \\(U=u_1\\otimes u_2\\) ，如果 \\(u_1=\\left[ \\beginarraya &c \\\\ b&d \\endarray\\right],u_2=\\left[ \\beginarraye &g \\\\ f&h \\endarray\\right]\\) ，那么， \\(U=\\left[ \\beginarraya\\left[ \\beginarraye &g \\\\ f&h \\endarray\\right] &c\\left[ \\beginarraye &g \\\\ f&h \\endarray\\right] \\\\ b\\left[ \\beginarraye &g \\\\ f&h \\endarray\\right]&d\\left[ \\beginarraye &g \\\\ f&h \\endarray\\right] \\endarray\\right]\\) ，这也就是张量积的算法。

对于图d来说，这是一个受控非门CNOT门，他的意思是，如果a是0，那么b保持不变，如果a是1，那么b就是变成相反的，比如 \\(|0\\rangle\\) 变成 \\(|1\\rangle\\) ，或者把 \\(|1\\rangle\\) 变成 \\(|0\\rangle\\) 。

即 \\(|00\\rangle to|00\\rangle,|01\\rangle to|01\\rangle,|10\\rangle to|11\\rangle,|11\\rangle to|10\\rangle\\) 。

用矩阵来描述就是 \\(\\left[\\beginarraycccc1 & 0 & 0 & 0 \\\\ 0 & 1 & 0 & 0 \\\\ 0 & 0 & 0 & 1 \\\\ 0 & 0 & 1 & 0\\endarray\\right]\\) 。

至此，主要的量子逻辑门就介绍完毕，如果想要动手实践的话，有阿里的量子计算云平台、华为的hiQ、IMB的IBM Q

参考资料

Quantume Mechanics & Quantume Computation Lecture 5