Alpha-Beta剪枝

Posted 2022-02-06 hanasaki

对于计算一个游戏的胜负，当且仅当后继状态中至少有一个必败状态时，本状态是必胜状态。但是这样既效率很低又不能计算出量化的形势。

因此需要改为双人零和博弈（如图所示）

 

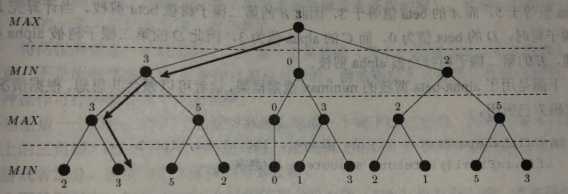
结点的值代表对于这个状态的甲方最终受益，显然甲方希望这个值尽可能大，乙方希望这个值尽可能小。

这就是极大极小搜索算法（minimax search），这个算法也对应着一种优化方法——Alpha-Beta剪枝。

 

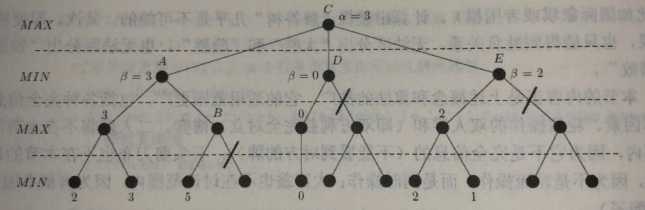
基本思想：每个MAX结点设置一个目前已知下界alpha，每个MIN节点设置一个目前已知上界beta。当计算一个MIN结点时，如果它的beta值小于等于其父结点的alpha值，则可以立即停止此结点的计算（alpha剪枝）；当计算一个MAX结点时，如果它的alpha结点大于等于其父结点的beta值，也可以立即停止此结点的计算（beta剪枝）。

int alphabeta(State& s, int player, int alpha, int beta) 
    if(s.isFinal()) return s.score;
    vector<State> children;
    s.expand(player, children);
    int n = children.size();
    for(int i = 0; i < n; i++) 
        int v = alphabeta(children[i], player^1, alpha, beta);
        if(!player) alpha = max(alpha, v); else beta = min(beta, v);
        if(beta <= alpha) break;
    
    return !player ? alpha : beta;