《入门经典》——6.21

Posted 2020-07-28 黑大帅之家

数据结构基础：

  所谓数据结构即整合繁杂数据使之变得排列井然有序的结构，我们最为熟悉的数组，其实就是一种数据结构，它本质上是一种线性表，即“所有的元素排成一行”，同为线性表的数据结构还有队列、栈、链表等，通常在处理一些环状结构的时候，我们从任意一点截断，便可将其转化为线性表。

 

  队列：

  卡片游戏：桌上有一叠拍，从第一张牌(即位于顶面的牌)开始从上往下一次编号为1~n。当至少还剩两张牌时进行如下操作：把第一张牌扔掉，然后把新的第一张放到整叠牌的最后。输入n，输出每次扔掉的牌，以及最后剩下的牌。

  样例输入：7.

  样例输出：1 3 5 7 4 2 6

  分析：观察这个过程，它非常像一个长长的队伍，队首的人走了，然后队首的人又来到了队尾……其实我们在《啊哈算法》一书的笔记专栏中介绍了这两种线性结构，它们都可以基于c和指针来完成模拟实现，这里主要介绍更为常见的c++中STL(标准模板库)的实现。

  具体用法如下：

 

 #include<cstdio>

#include<queue>

using namespace std;

queue<int> q;//队列操作0，定义。

 

int main()

{

    int n;

    scanf("%d",&n);

    for(int i = 1;i <= n;i++)  q.push(i);//队列操作1，向队尾添加元素

 

    while( !q.empty() )  //队列操作2，判断队列是否为空

    {

        printf("%d ",q.front()); //队列操作3，返回队列首元素

        q.pop();                //队列操作4，抛弃队列首元素

        q.push(q.front());

        q.pop();

    }

 

    return 0;

}

 

 

  栈：

  Ex2：

 

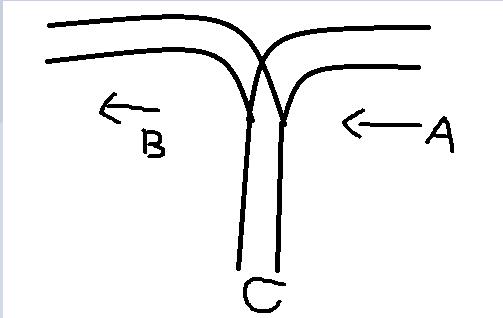
  某城市有一个火车站，如图。有n节车厢从A方向驶入车站，按进站顺序编号为1~n。你的任务是让它们按照某种特定的顺序进入B方向的铁轨并驶出车站。为了重组车厢，你可以借助中转站C。这是一个可以停放任意多节车厢的车站，但由于末端封顶，驶入C的车厢必须按照相反的顺序驶出C。对于每个车厢，一旦从A移入C，就不能再回到A了；一旦从C移入B，就不能回到C了。换句话说，在任意时刻，只有两种选择：A->C和C->B.

  分析：可以说火车轨道问题是生活中非常贴合栈这个数据模型的了，栈还可以看成这样一个具体例子：存羽毛球或者存乒乓球的盒子、存薯片的圆柱体包装，我们都不难概括出栈的一条性质，先进栈的后出栈。

  回到这个问题，中转站C就是一个奠定的栈模型。下面我们开始模拟判断方案过程。

  我们用两个变量A、B来分别表示模拟过程中A、B站这在进行匹配的下标。同时A还有表示标号的作用。

  它的匹配模拟过程如下。

  先判断A站中的头元素是否等于B站当前正在匹配的元素，如果相同，我们将这个元素入栈然后再出栈即可，两个位置变量A、B均加1.

  如果不相等，先不要着急将A站的头元素压入栈，应该先判断栈顶元素是否能够和B站正在匹配的元素相匹配，如果匹配，则弹出栈顶元素。

  经过如上的两个判断，在进行压栈操作。

  如果前三个步骤都没有进行，说明现在A站已经空了，栈没有空但是却无法进行匹配，表明不存在何时的排列方案。

  简单的参考代码如下。

  #include<cstdio>

#include<stack>

using namespace std;

const int maxn = 1000 + 5;

int n , target[maxn];

 

int main()

{

    while(scanf("%d",&n) != EOF)

    {

        stack<int> s;

           for(int i = 1;i <= n;i++)

              scanf("%d",&target[i]);

        int A,B;

        A = B = 1;

        int ok = 1;

        while(B <= n)

        {

               if (A == target[B]) {A++ , B++;}

               else if(!s.empty() && s.top() == target[B]){s.pop() , B++;}

               else if(A <= n)  {s.push(A++);}

               else  {ok = 0 ; break;}

        }

 

        printf("%s\\n",ok ? "Yes" : "No");

 

    }

}