线性方程组的迭代求解算法——原理
Posted fengqiao
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性方程组的迭代求解算法——原理相关的知识,希望对你有一定的参考价值。
- 迭代法的一般形式(对于Ax=b的一般形式)
- 迭代格式
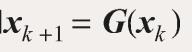
- G称为迭代算子
- 由迭代格式得到迭代序列
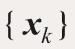
- 如迭代序列收敛于方程组的精确解,则称此迭代格式收敛
- 迭代格式的构造;将方程组改写成如下形式,如令A=B-C
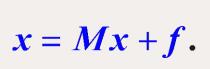
- 迭代格式
- Jacobi迭代:
- 算法实现:线性方程组迭代求解——Jacobi迭代算法(Python实现)
- 令A=D-L-U
- Jacobi迭代格式
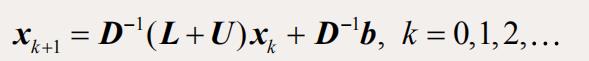
- Jacobi迭代矩阵:
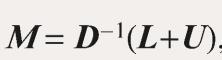
- 算法实现:线性方程组迭代求解——Jacobi迭代算法(Python实现)
- Gauss-Seidel迭代
- Gauss-Seidel迭代格式
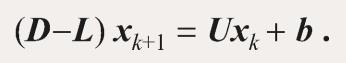
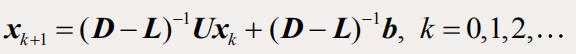
- Gauss-Seidel迭代矩阵
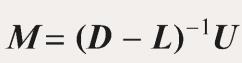
- Gauss-Seidel迭代格式
- 迭代算法的收敛性
- 迭代格式的收敛性:
- 迭代格式对任意初始量都收敛的充要条件是(也就是M的谱半径小于1)
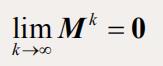
- 如果A是绝对行(列)对角占优,则Jacobi迭代格式、Gauss-Seidel迭代格式都收敛
- 如果A是实对称矩阵,则Gauss-Seidel迭代格式收敛
- 迭代格式对任意初始量都收敛的充要条件是(也就是M的谱半径小于1)
- 迭代格式的收敛速度:取决于M的谱半径大小,M的谱半径越小,收敛速度越快。
- 迭代格式的误差估计:

- 迭代格式的收敛性:
以上是关于线性方程组的迭代求解算法——原理的主要内容,如果未能解决你的问题,请参考以下文章