线性回归(非矩阵实现)
Posted liualex1109
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性回归(非矩阵实现)相关的知识,希望对你有一定的参考价值。
1 import numpy as np 2 import pandas as pd
#读取数据 points = np.genfromtxt(‘data.csv‘,dtype=np.double,delimiter=",") print(points)
[[ 32.50234527 31.70700585] [ 53.42680403 68.77759598] [ 61.53035803 62.5623823 ] [ 47.47563963 71.54663223] [ 59.81320787 87.23092513] [ 55.14218841 78.21151827] [ 52.21179669 79.64197305] [ 39.29956669 59.17148932] [ 48.10504169 75.3312423 ] [ 52.55001444 71.30087989] [ 45.41973014 55.16567715] [ 54.35163488 82.47884676] [ 44.1640495 62.00892325] [ 58.16847072 75.39287043] [ 56.72720806 81.43619216] [ 48.95588857 60.72360244] [ 44.68719623 82.89250373] [ 60.29732685 97.37989686] [ 45.61864377 48.84715332] [ 38.81681754 56.87721319] [ 66.18981661 83.87856466] [ 65.41605175 118.5912173 ] [ 47.48120861 57.25181946] [ 41.57564262 51.39174408] [ 51.84518691 75.38065167] [ 59.37082201 74.76556403] [ 57.31000344 95.45505292] [ 63.61556125 95.22936602] [ 46.73761941 79.05240617] [ 50.55676015 83.43207142] [ 52.22399609 63.35879032] [ 35.56783005 41.4128853 ] [ 42.43647694 76.61734128] [ 58.16454011 96.76956643] [ 57.50444762 74.08413012] [ 45.44053073 66.58814441] [ 61.89622268 77.76848242] [ 33.09383174 50.71958891] [ 36.43600951 62.12457082] [ 37.67565486 60.81024665] [ 44.55560838 52.68298337] [ 43.31828263 58.56982472] [ 50.07314563 82.90598149] [ 43.87061265 61.4247098 ] [ 62.99748075 115.2441528 ] [ 32.66904376 45.57058882] [ 40.16689901 54.0840548 ] [ 53.57507753 87.99445276] [ 33.86421497 52.72549438] [ 64.70713867 93.57611869] [ 38.11982403 80.16627545] [ 44.50253806 65.10171157] [ 40.59953838 65.56230126] [ 41.72067636 65.28088692] [ 51.08863468 73.43464155] [ 55.0780959 71.13972786] [ 41.37772653 79.10282968] [ 62.49469743 86.52053844] [ 49.20388754 84.74269781] [ 41.10268519 59.35885025] [ 41.18201611 61.68403752] [ 50.18638949 69.84760416] [ 52.37844622 86.09829121] [ 50.13548549 59.10883927] [ 33.64470601 69.89968164] [ 39.55790122 44.86249071] [ 56.13038882 85.49806778] [ 57.36205213 95.53668685] [ 60.26921439 70.25193442] [ 35.67809389 52.72173496] [ 31.588117 50.39267014] [ 53.66093226 63.64239878] [ 46.68222865 72.24725107] [ 43.10782022 57.81251298] [ 70.34607562 104.25710159] [ 44.49285588 86.64202032] [ 57.5045333 91.486778 ] [ 36.93007661 55.23166089] [ 55.80573336 79.55043668] [ 38.95476907 44.84712424] [ 56.9012147 80.20752314] [ 56.86890066 83.14274979] [ 34.3331247 55.72348926] [ 59.04974121 77.63418251] [ 57.78822399 99.05141484] [ 54.28232871 79.12064627] [ 51.0887199 69.58889785] [ 50.28283635 69.51050331] [ 44.21174175 73.68756432] [ 38.00548801 61.36690454] [ 32.94047994 67.17065577] [ 53.69163957 85.66820315] [ 68.76573427 114.85387123] [ 46.2309665 90.12357207] [ 68.31936082 97.91982104] [ 50.03017434 81.53699078] [ 49.23976534 72.11183247] [ 50.03957594 85.23200734] [ 48.14985889 66.22495789] [ 25.12848465 53.45439421]]
#定义损失函数 loss = ∑(y-*(wx-b))² / m def get_loss_function_sum(w,b,points): totalError=0 m = len(points) for i in range(m): x = points[i,0] y = points[i,1] totalError += (y - (w * x - b)) ** 2 return totalError / m
#梯度下降 dw = ∑(y-(wx-b))*x / m, db = ∑(y-(wx-b)) / m def gradient_descent(w_current,b_current,points,learning_rate): dw = 0 db = 0 m = len(points) for i in range(m): x = points[i,0] y = points[i,1] dw += -(2 / m) * x * (y - (w_current * x - b_current)) db += -(2 / m) * (y - (w_current * x - b_current)) w = w_current - (learning_rate * dw ) b = b_current - (learning_rate * db ) return w,b
def runner(w_start,b_start,points,learning_rate,itera_num): w = w_start b = b_start for i in range(itera_num): w,b = gradient_descent(w,b,points,learning_rate) return w,b
#注:learning rate要足够小
w,b = runner(0,0,points,0.0001,10000) print("totalError:" + str(get_loss_function_sum(w,b,points)))
totalError:113.08177442339228
from matplotlib import pyplot as plt points = np.array(points) x = points[:,0] y = points[:,1] f = w * x + b plt.title("data") plt.xlabel("x") plt.ylabel("y") plt.scatter(x,y)#数据集 plt.plot(x,f)#拟合曲线 plt.show()
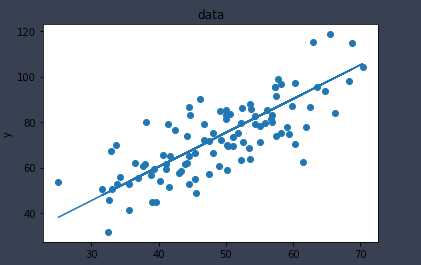
以上是关于线性回归(非矩阵实现)的主要内容,如果未能解决你的问题,请参考以下文章