leetcode-hard-array- -NO

Posted 2022-01-18 rosyyy

mycode  time limited

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        final = 0
        for i in range(1,len(height)):
            temp = []
            for j in range(i):
                h = min(height[j],height[i])
                width = i - j
                temp.append(h*width)
            final = max(final,max(temp))
        return final
        

 

参考：

把求水的容量转换成求面积

假设： 第i条和第j条(i < j)线和x轴围起来面积最大，那么最大面积为Sij = min(ai, aj) * (j - i);

那么：

• 在j的右边没有比他更高的线

• 在i的左边也没有比他更高的线

证明 ：
反证法：
如果在j的右边存在比他高的线为第k第线， 那么Sik = min(ai, ak) *(k - i)， 由于k > j，所以Sik > Sij，与Sij最大的条件矛盾。
同理可证在i的左边也没有比他更高的线。

从上面说的性质可以说明， 从头和尾分别向中间遍历a1, a2, ..., an, 如果遍历的线比前面的高，则更新当前最高，并算出面积与之前存的最大面积比较，当前更大则更新，否之则跳过。

但有一个问题： 头和尾哪个先向中间遍历呢？

--高度矮的个。 因为如果高的向中间移动了，那矮的那边就不可能遍历到高的现在遍历的那个点了，就可能找不到最大面积。

例如：

 

 

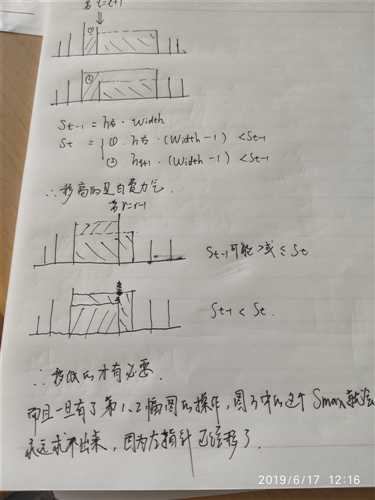
这也是动态规划的用法。

class Solution(object):
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        l = 0 
        r = len(height)-1
        res = 0
        while l < r :
            h = min(height[l] , height[r])
            w = r - l
            res = max(res , h*w)
            #print(l,r,res)
            if height[l] < height[r]:
                l += 1
            else:
                r -= 1
        return res