二叉树的基本操作

Posted 2022-01-13 chenglc

二叉树的基本操作包含：

　　判断是否为空，获取节点数，先跟遍历，中跟遍历，后根遍历，层级遍历，查找元素

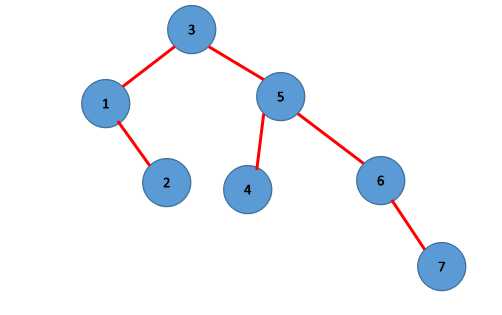
二叉树结构

public class Node 
    Object value; //结点值
    Node leftChild;//左子树的引用
    Node rightChild;//右子树的引用

    public Node(Object value) 
        super();
        this.value = value;
    

    public Node(Object value, Node leftChild, Node rightChild) 
        super();
        this.value = value;
        this.leftChild = leftChild;
        this.rightChild = rightChild;
    

    @Override
    public String toString() 
        return "Node" +
                "value=" + value +
                ", leftChild=" + leftChild +
                ", rightChild=" + rightChild +
                ‘‘;
    

判断是否为空树：

   public boolean isEmpty() 
        return root == null;
    

获取节点数量：

 public int size(Node root) 
        if (root == null)
            return 0;
        int left = size(root.leftChild);
        int right = size(root.rightChild);
        return left + right + 1;
    

获取高度：

    public int getHeight(Node root) 
        if (root == null)
            return 0;
        int left = getHeight(root.leftChild);
        int right = getHeight(root.rightChild);
        return Math.max(left, right) + 1;
    

先根遍历递归：

 public void preOrderTraverse(Node root) 
        if (root == null)
            return;
        //打印根节点
        System.out.print(root.value + "  ");
        //创建左子树，进行先跟遍历
        preOrderTraverse(root.leftChild);
        //创建右子树，进行先跟遍历
        preOrderTraverse(root.rightChild);
    

中跟递归：

   public void inOrderTraverse(Node root) 
        //出口
        if (root == null)
            return;
        //遍历左子树
        inOrderTraverse(root.leftChild);
        //遍历根
        System.out.print(root.value + "  ");
        //遍历右子树
        inOrderTraverse(root.rightChild);
    

中跟非递归：

  @Override
    public void inOrderByStack() 
        Stack<Node> stack = new Stack<>();
        Node temp = root;
        while (temp != null || !stack.isEmpty()) 
            while (temp != null) 
                stack.push(temp);
                temp = temp.leftChild;
            
            if (!stack.isEmpty()) 
                temp = stack.pop();
                System.out.print(temp.value + "  ");
                temp = temp.rightChild;
            
        
    

后跟递归：

 public void postOrderTraverse(Node root) 
        //出口
        if (root == null)
            return;
        //先左
        postOrderTraverse(root.leftChild);
        //再右
        postOrderTraverse(root.rightChild);
        //后根
        System.out.print(root.value + "  ");
    

层次遍历：

 public void levelOrderByStack() 
        if (root == null)
            return;
        Queue<Node> queue = new LinkedList<>();
        queue.add(root);
        int len;
        while ((len = queue.size()) != 0) 
            for (int i = 0; i < len; i++) 
                Node temp = queue.poll();
                System.out.print(temp.value + "  ");
                if (temp.leftChild != null)
                    queue.add(temp.leftChild);
                if (temp.rightChild != null)
                    queue.add(temp.rightChild);
            
        
    

递归查找元素：

 public Node findKey1(int value, Node root) 
        if (root == null)
            return null;
        if (root.value.equals(value))
            return root;
        Node left = findKey1(value, root.leftChild);
        Node right = findKey1(value, root.rightChild);
        if (left != null)
            return left;
        if (right != null)
            return right;
        return null;