P3899 [湖南集训]谈笑风生 (线段树合并）

Posted 2022-01-08 zhangbuang

题目描述

设 T 为一棵有根树，我们做如下的定义：

• 设 a 和 b 为 T 中的两个不同节点。如果 a 是 b 的祖先，那么称“a 比 b 不知道高明到哪里去了”。

• 设 a 和 b 为 T 中的两个不同节点。如果 a 与 b 在树上的距离不超过某个给定常数 x，那么称“a 与 b 谈笑风生”。

给定一棵 n 个节点的有根树 T，节点的编号为 1 ∼ n，根节点为 1 号节点。你需要回答 q 个询问，询问给定两个整数 p 和 k，问有多少个有序三元组 (a; b; c) 满足：

1. a、 b 和 c 为 T 中三个不同的点，且 a 为 p 号节点；

2. a 和 b 都比 c 不知道高明到哪里去了；

3. a 和 b 谈笑风生。这里谈笑风生中的常数为给定的 k。

输入输出格式

输入格式：

 

输入文件的第一行含有两个正整数 n 和 q，分别代表有根树的点数与询问的个数。

接下来 n − 1 行，每行描述一条树上的边。每行含有两个整数 u 和 v，代表在节点 u 和 v 之间有一条边。

接下来 q 行，每行描述一个操作。第 i 行含有两个整数，分别表示第 i 个询问的 p 和 k。

 

输出格式：

 

输出 q 行，每行对应一个询问，代表询问的答案。

 

输入输出样例

输入样例#1： 复制

5 3
1 2
1 3
2 4
4 5
2 2
4 1
2 3

输出样例#1： 复制

3
1
3

说明

样例中的树如下图所示：

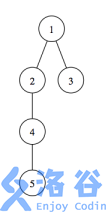
对于第一个和第三个询问，合法的三元组有 (2,1,4)、 (2,1,5) 和 (2,4,5)。

对于第二个询问，合法的三元组只有 (4,2,5)。

所有测试点的数据规模如下：

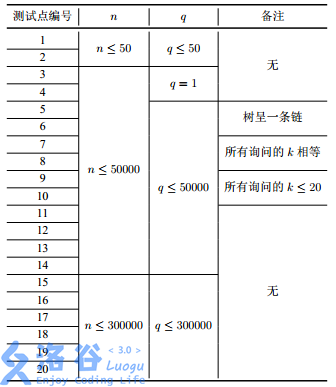
对于全部测试数据的所有询问， 1 ≤ p ≤ n， 1 ≤ k ≤ n.

---

---

---

---

---

---

 

开始想的是查询某一个节点的子树内距离他为k的节点的size和

发现这样并不好做

开始想的是查询某一个节点的子树内深度的k的节点的size和

这样一来就很好做了，想想一个节点的儿子节点有的话，那他也有，

就是线段树合并了吧。

：：：好像合并的函数并不能写引用

：：：好像要线upd自身，再合并，但是不这样也能a， 是数据太水吗

---

---

---

---

---

---

 

 

  1 #include"bits/stdc++.h"
  2 #define sd(x) scanf("%d",&(x));
  3 #define sf(x) scanf("%lf",&(x));
  4 #define sld(x) scanf("%lld",&(x));
  5 typedef long long ll;
  6 
  7 using namespace std;
  8 const int N = 400000;
  9 int n,m;
 10 vector<int > v[N];
 11 int deep[N];
 12 int root[N];
 13 int ls[N*30],rs[N*30];
 14 long long  tr[N*30];
 15 int sze[N];
 16 
 17 int tot;
 18 
 19 int  hb(int x,int y,int l,int r)
 20 
 21     if(!x || !y)
 22     
 23         return x+y;
 24     
 25     int t=++tot;
 26     tr[t] =tr[x]+ tr[y];
 27     if(l==r)
 28     
 29      return t ;
 30     
 31 
 32     int mid = l+r>>1;
 33     ls[t] = hb(ls[x],ls[y],l,mid);
 34     rs[t] = hb(rs[x],rs[y],mid+1,r);
 35     return t;
 36 
 37 
 38 void upd(int &x,int l,int r,int p,int v)
 39 
 40     if(!x)x=++tot;
 41     tr[x] += v;
 42     if(l==r)return ;
 43     int mid = l+r>>1;
 44     if(p<=mid)upd(ls[x],l,mid,p,v);
 45     else upd(rs[x],mid+1,r,p,v);
 46 
 47 
 48 long long  que(int x,int l,int r,int L,int R)
 49 
 50     if(!x)return 0;
 51     if(L<=l && r<=R)return tr[x];
 52     int mid = l+r>>1;
 53     long long res=0;
 54     if(L<=mid)res += que(ls[x],l,mid,L,R);
 55     if(R>mid) res += que(rs[x],mid+1,r,L,R);
 56     return res;
 57 
 58 void dfs(int x,int fa)
 59 
 60     deep[x] = deep[fa]+1; sze[x] = 1;
 61     for(auto i:v[x])if(i!=fa)
 62     
 63         dfs(i,x); sze[x] += sze[i];
 64        // hb(root[x],root[i],1,n);
 65     
 66     upd(root[x],1,n,deep[x],sze[x]-1);
 67      for(auto i:v[x])if(i!=fa)
 68     
 69          root[x]=hb(root[x],root[i],1,n);
 70     
 71    // cout<<"UPD: "<<x<<" " <<deep[x]<<" "<<sze[x]<<endl;
 72      //   if(x==1)cout<<que(root[1],1,n,1,1)<<endl;;
 73 
 74 
 75 
 76 
 77 signed main()
 78 
 79     scanf("%d %d",&n,&m);
 80     for(int i=1;i<n;i++)
 81     
 82         int l,r;
 83         scanf("%d %d",&l,&r);
 84         v[l].push_back(r);
 85         v[r].push_back(l);
 86     
 87     for(int i=1;i<=n;i++)root[i]=++tot;
 88     dfs(1,0);
 89    // //for(int i=1;i<=n;i++)cout<<root[i]<<" "<<tr[root[i]]<<endl;;
 90    //  puts("");
 91    // cout<<que(root[1],1,n,2,2)<<endl;;
 92 
 93     while(m--)
 94     
 95         int p,k;        scanf("%d %d",&p,&k);
 96 
 97         long long  ans = 0;
 98         ans += min(k,deep[p]-1)*1ll*(sze[p]-1);
 99        // cout<<ans<<endl;
100         ans += que(root[p],1,n,deep[p]+1,deep[p]+k);
101         printf("%lld\n",ans);
102 
103     
104 
105    return 0;
106 
107 
108 
109 
110