Codeforces Round #564 (Div. 2)

Posted 2022-01-07 sienna

contest传送门

A

神秘点赞事件，要水得优雅\\(2,3,5\\)

#include <bits/stdc++.h>

using namespace std;

int main()
    ios::sync_with_stdio();
    cin.tie(0);
    int x,y,z;
    cin>>x>>y>>z;
    if(x>y+z) cout<<'+';
    else if(y>x+z) cout<<'-';
    else cout<<(z?'?':'0');
    cout<<'\\n';
    return 0;

B

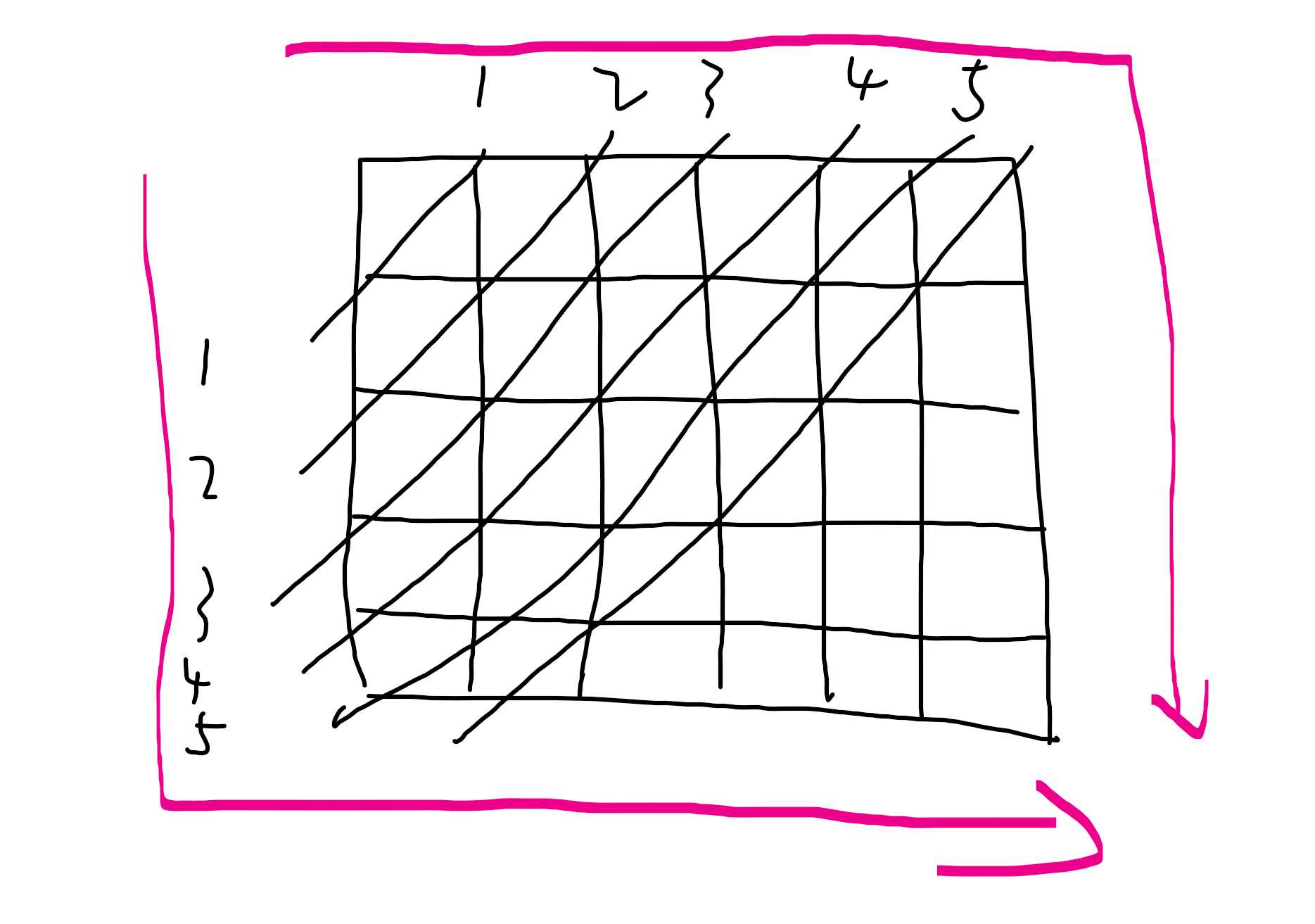
有意思的一道规律题，如图，以左上为起点的话，对角线上的距离到该点距离依次增大，那么只需要选择喜欢的角度输出就可以了。m = n/2+1是可以证明的(猜)。

#include <bits/stdc++.h>

using namespace std;

int main()
    ios::sync_with_stdio();
    cin.tie(0);
    int n;
    cin>>n;
    int m = n/2+1;
    cout<<m<<'\\n';
    for(int i=1;i<=m;i++) cout<<1<<' '<<i<<'\\n';
    for(int i=2;i<=n-m+1;i++) cout<<i<<' '<<m<<'\\n';
    return 0;

C

吃着碗里一定要看着锅里。前n个数据没用，随便读一下就行。这题可以逆向思维。假设n为9。当你需要插入9时，1-8的序列已经排好了。所以我们只需要关心1插入的时机，且插入i时，i+1可以拿到手上or已经在手上了。不难推导出，从max(i-a[i]+1)开始插入序列刚好可以让‘最难‘拿到的牌，在插入a[i]-1时刚好拿到手中。
特殊情况就是牌堆的后半部分是成序的，那就只用在牌堆的前半部分做上述操作。

#include <bits/stdc++.h>

using namespace std;
const int N = 2e5+10;
int a[N];
int main()
    ios::sync_with_stdio();
    cin.tie(0);
    int n;
    cin>>n;
    for(int i=0;i<n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) cin>>a[i];
    int x = n,y = a[n],ans=0,now=n;
    for(;y&&a[x]==y;x--,y--) ;
    for(int i=1;!y&&a[i]!=1;i++)
        if(a[i]&&i>=a[i]-a[n]) y=1;
    if(!y) now -= a[n];
    for(int i=1;i<=now;i++)
        if(a[i]) ans = max(ans,i-a[i]+1);
    cout<<ans+now<<'\\n';
    return 0;

D

补题。

把一棵树的点放在圆上，使所有的边不相交。问多少方案数。
没有边时，答案乘上段数
有边时，答案乘上边数

#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+10;
const long long mod=998244353;

long long ct[maxn],seg=1,ans=1;
bool vis[maxn];
int x[maxn],y[maxn];
vector<int>V[maxn];
vector<int>::iterator it;

void dfs(int p)
    if(vis[p])return;
    vis[p]=1;
    for(int i=0;i<(int)V[p].size();i++)
        int to=V[p][i];
        if(vis[to])continue;
        ct[p]++;
        ct[to]++;
        ans=ans*ct[p]%mod;
        seg++;
        dfs(to);
    


int main()
    ios::sync_with_stdio();
    cin.tie(0);
    int n;cin>>n;
    for(int i=1;i<n;i++)
        scanf("%d%d",&x[i],&y[i]);
        V[x[i]].push_back(y[i]);
        V[y[i]].push_back(x[i]);
    
    seg=1;
    for(int i=1;i<=n;i++)
        if(ct[i]==0)ans*=seg%mod;
        dfs(i);
    
    cout<<((long long)ans*n%mod)<<endl;

E(easy&hard)

确认过眼神，是我不会的概率dp

F

NXN的迷宫。分别从第一行和第一列进入，只能朝同一个方向移动。给出数个从(1,i)和(i,1)开始到(n,i)和(i,n)的情况。求如何架设传送门。
每对传送门进入后可达到相对的格子，但是行进方向不变。
问题模拟起来感觉很复杂，所以一定要让其有序。
因为架设一对传送门后，所有进过这两个格点的路径都会受到影响，所以1~n枚举出口使改变后的行列后移，变得有序。
如，在第1,4行架设传送门，第i行出发想要到达1出口的视为从第4行开始。列也相同。
由此可知，传送门架设的顺序是依次往右下方向，因为遍历1出口时，需要经过其他行的路径经过传送门已经默认从1开始。自然不会破坏前面架设门的相对关系。

#include<bits/stdc++.h>

using namespace std;
const int maxn=1e3+10;
int n,x,y,a[maxn],b[maxn],tot=0;
struct node
    int a,b,c,d;
    node();
    node(int aa,int bb,int cc,int dd)
        a=aa;b=bb;c=cc;d=dd;
    
ans[maxn];

int main()
    ios::sync_with_stdio();
    cin.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) cin>>b[i];
    for(int i=1;i<=n;i++)
        if(a[i]==i&&b[i]==i) continue;
        for(int j=i;j<=n;j++)
            if(a[j]==i) 
                swap(a[i],a[j]);x=j;
                break;
        
        for(int j=i;j<=n;j++)
            if(b[j]==i) 
                swap(b[i],b[j]);y=j;
                break;
        
        ans[++tot]=node(x,i,i,y);
    
    cout<<tot<<'\\n';
    for(int i=1;i<=tot;i++) cout<<ans[i].a<<' '<<ans[i].b<<' '<<ans[i].c<<' '<<ans[i].d<<'\\n';