非线性方程求解的常用方法

Posted 2022-01-04 itero

公式法

对于一元二次方程的一般形式：\\(ax^2 + bx + c = 0\\)

可以使用韦达公式来求方程的两个实数解\\(x = \\frac-b+\\sqrtb^2-4ac2a\\)，两根之和\\(x_1 + x_2 = -\\fracba\\) ，两根之积\\(x_1 * x_2 = \\fracca\\)，当Δ<0时，得到的是不相等的两个虚数根，\\(x = \\frac-b+i\\sqrt4ac-b^22a\\)，一元三次方程有卡尔丹公式和盛金公式。

二分逼近法

对一元二次方程f(x)来说，给定区间[a, b]，如果f(a)<0, f(b)>0，则可以按照下列方法进行逼近：

1. 如果\\(f(\\fraca+b2)= 0\\)，则\\(\\fraca+b2\\)就是零点；
2. 如果\\(f(\\fraca+b2) < 0\\)，则零点在区间\\([\\fraca+b2, b]\\)上，令\\(a = \\fraca+b2\\)，继续从第1步开始判断；
3. 如果\\(f(\\fraca+b2) > 0\\)，则零点在区间\\([a, \\fraca+b2]\\)上，令\\(b = \\fraca+b2\\)，继续从第1步开始判断。

通常只要在精度允许的范围内逼近零时就可以结束二分逼近的过程。二分法的局限在于不能计算复根和重根。

牛顿迭代法

牛顿迭代法的数学原理

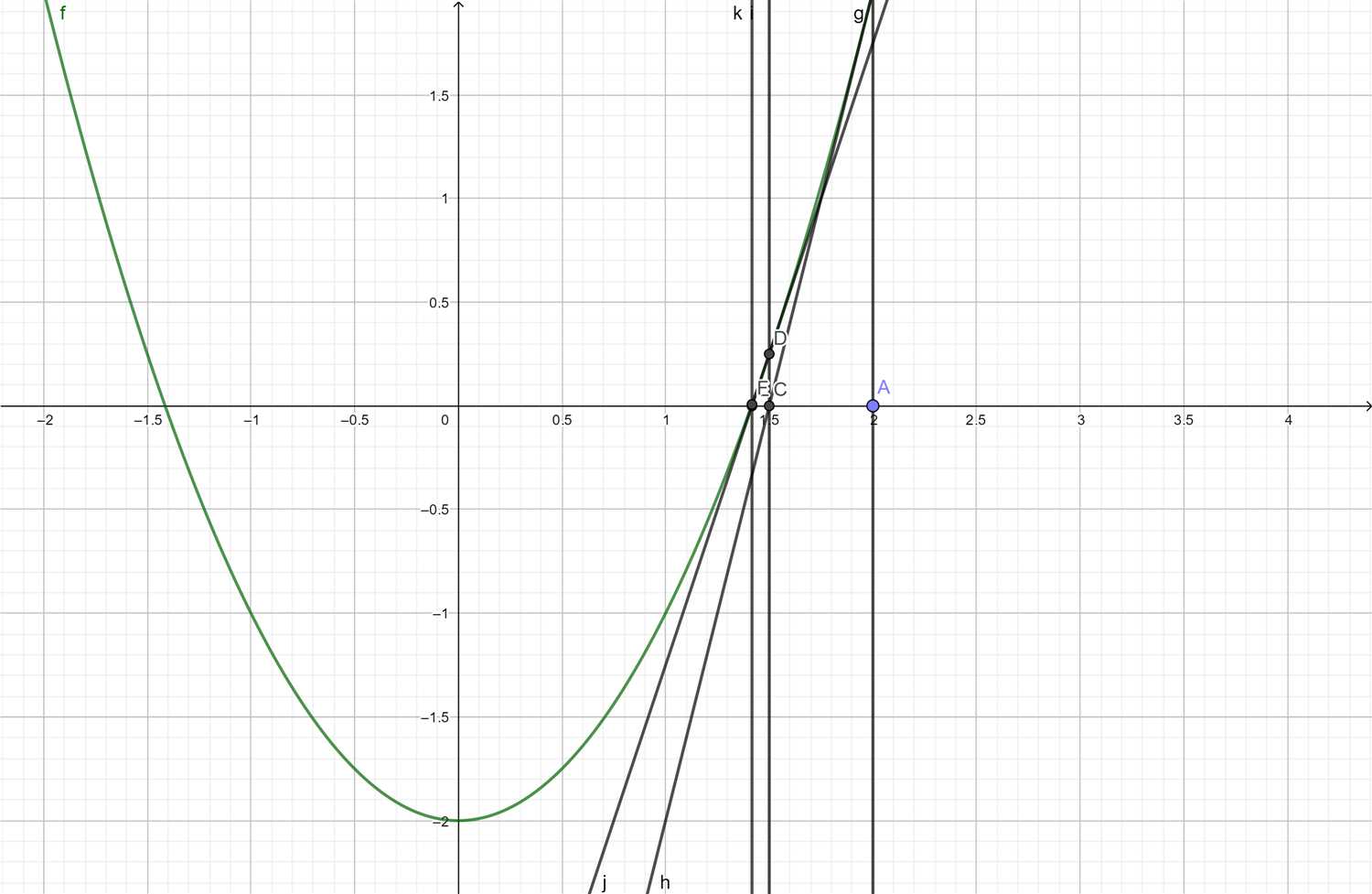
在x轴找一点\\(x_0\\)，过点\\(x_0\\)垂直于x轴做垂线，交\\(f(x)\\)于点\\(f(x_0)\\)，然后再过\\(f(x_0)\\)点做函数的切线，得到切线与x轴的交点记为\\(x_n+1\\)，一直循环下去，最终会得到根的近似值：

\\[x_n+1 = x_n - \\fracf(x_n)f'(x_n)\\]

此方法也可以用来根号的值，比如要求\\(\\sqrt c\\)的值，可以构造一个函数\\(f(x) = x^2 -c\\)，求这个函数的右根即是得到$\\sqrt c $的值。利用公式，

\\[设x_n = t，则 x_n+1 = t - \\fract^2 - c2t = \\fract+\\fracct2\\]

得到的\\(x_n+1 \\)设为新的t，带入公式，一直等到误差小于特定的值，再返回答案，得到的t就是开根的值。初始时可以令t=c，便于计算。这段函数的代码如下：

public static double sqrt(double c) 
    if(c < 0)
        return Double.NaN;
    double err = 1e-15;
    double t = c;
    while(Math.abs(t-c/t) > err*t)
        t = (c/t+t) / 2.0;
    return t;