Codeforces Round 563 (Div. 2) 题解
Posted 1000suns
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Codeforces Round 563 (Div. 2) 题解相关的知识,希望对你有一定的参考价值。
自己开了场镜像玩。
前三题大水题。D有点意思。E完全不会。F被题意杀了……然而还是不会。
不过看过(且看懂)了官方题解,所以这里是六题题解齐全的。
A
水题。给原序列排序,如果此时合法则直接输出,否则说明所有数相同,一定无解。
时间复杂度 $O(n\\log n)$。

#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<int,int> PII; const int maxn=100010; #define MP make_pair #define PB push_back #define lson o<<1,l,mid #define rson o<<1|1,mid+1,r #define FOR(i,a,b) for(int i=(a);i<=(b);i++) #define ROF(i,a,b) for(int i=(a);i>=(b);i--) #define MEM(x,v) memset(x,v,sizeof(x)) inline ll read() char ch=getchar();ll x=0,f=0; while(ch<‘0‘ || ch>‘9‘) f|=ch==‘-‘,ch=getchar(); while(ch>=‘0‘ && ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); return f?-x:x; int n,a[maxn],s1,s2; int main() n=read(); FOR(i,1,2*n) a[i]=read(); sort(a+1,a+2*n+1); FOR(i,1,n) s1+=a[i]; FOR(i,n+1,2*n) s2+=a[i]; if(s1==s2) printf("-1\\n"); else FOR(i,1,2*n) printf("%d ",a[i]);
B
水题。
首先,如果所有数的奇偶性都相同,那我们什么都不能做。
否则,如果两个数奇偶性不同,可以直接交换;如果两个数奇偶性相同,可以用一个奇偶性不同的作为中介交换。那么实际上就是任意两个数都能交换,排个序即可。
时间复杂度 $O(n\\log n)$。

#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<int,int> PII; const int maxn=100010; #define MP make_pair #define PB push_back #define lson o<<1,l,mid #define rson o<<1|1,mid+1,r #define FOR(i,a,b) for(int i=(a);i<=(b);i++) #define ROF(i,a,b) for(int i=(a);i>=(b);i--) #define MEM(x,v) memset(x,v,sizeof(x)) inline ll read() char ch=getchar();ll x=0,f=0; while(ch<‘0‘ || ch>‘9‘) f|=ch==‘-‘,ch=getchar(); while(ch>=‘0‘ && ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); return f?-x:x; int n,a[maxn]; bool hhh[2]; int main() n=read(); FOR(i,1,n) a[i]=read(),hhh[a[i]&1]=true; if(hhh[0] && hhh[1]) sort(a+1,a+n+1); FOR(i,1,n) printf("%d ",a[i]);
C
水题。
首先质数位置的值互不相同。一一编号即可。
对于合数(设为 $x$),可以任取它的一个质因子(设为 $p$),令 $a_x=a_p$。此时序列最大值不变,而两个互质的数的位置的值不可能相同。
我取的是最小质因子。
时间复杂度 $O(n)$。

#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<int,int> PII; const int maxn=100010; #define MP make_pair #define PB push_back #define lson o<<1,l,mid #define rson o<<1|1,mid+1,r #define FOR(i,a,b) for(int i=(a);i<=(b);i++) #define ROF(i,a,b) for(int i=(a);i>=(b);i--) #define MEM(x,v) memset(x,v,sizeof(x)) inline ll read() char ch=getchar();ll x=0,f=0; while(ch<‘0‘ || ch>‘9‘) f|=ch==‘-‘,ch=getchar(); while(ch>=‘0‘ && ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); return f?-x:x; int n,ans[maxn],pr[maxn],mn[maxn],pl,cnt; bool vis[maxn]; int main() n=read(); FOR(i,2,n) if(!vis[i]) pr[++pl]=i,ans[i]=++cnt; FOR(j,1,pl) if(i*pr[j]>n) break; vis[i*pr[j]]=true; mn[i*pr[j]]=pr[j]; if(i%pr[j]==0) break; FOR(i,2,n) if(mn[i]) ans[i]=ans[mn[i]]; FOR(i,2,n) printf("%d ",ans[i]);
D
有一点点小难度,但还是很水。
首先考虑这个序列的前缀异或和 $S$。那么对于任意的 $i$,有 $S_i\\ne x$;对于任意的 $i,j$($i\\ne j$),有 $S_i\\oplus x\\ne S_j$。
看第二条限制,发现如果选了 $a$,那么不能选 $a\\oplus x$;如果选了 $a\\oplus x$,那么不能选 $a$。对其它数没有影响。
所以可以在 $a,a\\oplus x$ 中任选一个作为前缀异或和。
最后用选出来的前缀异或和算出原序列。此时答案一定是最优。
时间复杂度 $O(2^n)$。

#include<bits/stdc++.h> using namespace std; typedef long long ll; typedef pair<int,int> PII; const int maxn=333333; #define MP make_pair #define PB push_back #define lson o<<1,l,mid #define rson o<<1|1,mid+1,r #define FOR(i,a,b) for(int i=(a);i<=(b);i++) #define ROF(i,a,b) for(int i=(a);i>=(b);i--) #define MEM(x,v) memset(x,v,sizeof(x)) inline ll read() char ch=getchar();ll x=0,f=0; while(ch<‘0‘ || ch>‘9‘) f|=ch==‘-‘,ch=getchar(); while(ch>=‘0‘ && ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar(); return f?-x:x; int n,x,lim,ans[maxn],al; bool vis[maxn]; int main() n=read();x=read(); lim=1<<n; FOR(i,1,lim-1) if(vis[i^x] || i==x) continue; vis[i]=true; ans[++al]=i; printf("%d\\n",al); FOR(i,1,al) printf("%d ",ans[i]^ans[i-1]);
E
太难了……难度 2500……
为此专门另开了篇博客:传送门
F
一开始以为不会给树的形态,一直在想……
这里给出轻重链剖分(俗称树剖)的做法。
首先一开始肯定要查询 $1$ 到 $x$ 的距离。这个就是 $x$ 的深度 $dep_x$。(定义 $1$ 的深度为 $0$)
现在假设我们已经确定 $x$ 在 $u$ 的子树中。一开始 $u=1$。
我们沿着 $u$ 的重儿子一直跳,跳到叶子结点 $v$。(实际上不用真跳,可以实现成 $O(1)$)
接下来,再考虑 $y=lca(x,v)$。(从官方题解盗张图)
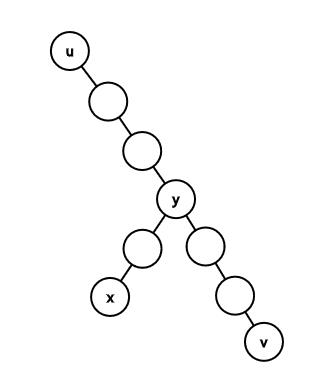
首先,询问一次 $dis(x,v)$。由于 $dis(x,v)=dep_x+dep_v-2dep_y$,而 $dis(x,v)$ 已知,$dep_x$ 已知,$dep_v$ 已知,可以算出 $dep_y$。那么 $y$ 也已知。
如果 $dep_x=dep_y$ 那么 $x=y$。 否则我们再询问 $y$ 到 $x$ 路径上的第二个点 $www$(没名字了),然后接下来就可以在 $u=www$ 的子树中寻找答案了。
对于最后一次查找,只用 $1$ 次询问,其它要 $2$ 次询问。预处理 $dep_x$ 要 $1$ 次询问。由于 $sz[www]\\le sz[y]/2\\le sz[u]$,所以每次 $u$ 的大小都会缩小一半。
那么总共要 $2\\log n$ 次询问。时间复杂度 $O(n)$。
代码咕着,会来补的。
以上是关于Codeforces Round 563 (Div. 2) 题解的主要内容,如果未能解决你的问题,请参考以下文章
