Codeforces Round #553 B. Dima and a Bad XOR

Posted 2021-12-20 happy-medge

题面：

传送门 

题目描述：

题意很简单：在一个N*M的矩阵中(N行M列)，问是否可以：每行选一个整数，使他们的异或和大于0。如果不可以，输出"NIE"；如果可以，输出"TAK"，并输出选择的整数。

 

题目分析：

这道题刚开始想直接暴力，但看到复杂度竟然是O(500^500)，就怂了??。到后面仔细观察，发现题目有个数据：每个数小于1024，也就是2^10次方。会不会跟数位有关？后面分析了一下，果然是，但没时间做了??，不过结束后还是A出来了。

 

异或（求大佬无视）：转化为二进制后按位异或，相同位会变为0，不同位会变为1。比如3和5进行异或，3的二进制是11，5的二进制是101，结果就是110：

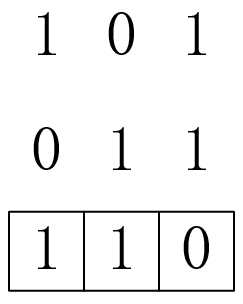
(注：上面最右边的第一位由于是相同位（1，1），所以变成了0，第二位是不同位，所以变成了1，第三位：因为11没有第三位，所以补一个0，变成011，然后再进行按位异或。结果就是110，然后110会转化位十进制，也就是最终结果是6，即3和5异或是6）

 

为什么要强调这个异或呢？其实重点不在于异或的规则，而在于异或转化为二进制处理的思想。我们把结果按照二进制来看：假如我们选出来的整数全部进行异或后，得到的结果转化位二进制，每个二进制位至少有一个不为0，就可以输出答案了。然后我们再看看题目数据限制：每个整数不超过1024，也就是说异或出来的结果也不超过1024，即结果的二进制位最多为9位。算下来时间复杂度是O(9*500*500)，1e6左右，不会超时。所以，我们的核心思想就是：枚举结果的二进制位，尽量使结果中的二进制位含有1。剩下来就是贪心了。

 

我们再分析一下，会发现其实很容易得到这样的分类：假如当前是想让结果的第num个二进制位为1，那么，就会有：1.某一行的全部整数在第num个二进制位为1，2.某一行的全部整数在第num个二进制位为0，3.某一行的部分整数在第num个二进制位为1，另一部分在第num个二进制位为0。按照这三类，我们就可以分析这三类情况对 “异或后结果的第num个二进制位为1” 的贡献：首先，第二种情况没有任何贡献；其次，如果第一种情况是有奇数行，那么只需要使符合第三种情况的行选出来的整数在第num个二进制位为0，就可以让结果的第num个二进制位为1；如果第一种情况是有偶数行，那么只需要选出符合第三种情况的其中一行，使这一行选出的整数第num个二进制位为1，第三种情况剩下的行选出来的整数在第num个二进制位为0就行了。

 

 

AC代码（代码巨丑）：

  1 #include <cstdio>
  2 #include <iostream>
  3 #include <cstring>
  4 #include <algorithm>
  5 using namespace std;
  6 int n, m;
  7 int G[505][505];
  8 struct node
  9     int odd, even;
 10     int is;
 11 ;
 12 node row[505];
 13 
 14 int main()
 15     scanf("%d%d", &n, &m);
 16     for(int i = 0; i < n; i++)
 17         for(int j = 0; j < m; j++)
 18             scanf("%d", &G[i][j]);
 19         
 20     
 21     
 22     int t;
 23     for(int num = 0; num <= 8; num++)  //枚举结果的位
 24         //分类
 25         for(int i = 0; i < n; i++)
 26             row[i].odd = 0, row[i].even = 0;
 27             for(int j = 0; j < m; j++)
 28                 t = (G[i][j] >> num);     //取出整数的第num位
 29                 if(t & 1) row[i].odd = 1;  
 30                 else row[i].even = 1;
 31             
 32             if(row[i].even == 1 && row[i].odd == 1)
 33                 row[i].is = 2;     //第三种情况
 34             
 35             else if(row[i].even == 1)
 36                 row[i].is = 0;     //第一种情况
 37             
 38             else row[i].is = 1;    //第二种情况
 39         
 40         
 41         int flag = 0;      //标记
 42         int cnt = 0;       //统计第一种情况个数 
 43         for(int i = 0; i < n; i++)
 44             if(row[i].is == 1) cnt++;
 45         
 46         if(cnt % 2 == 1) flag = 1;   //第一种情况为奇数个
 47         
 48         for(int i = 0; i < n; i++)
 49             if(row[i].is == 2)      //有符合第三种情况的行，也必定可以产生贡献
 50                 flag = 1;
 51                 break;
 52             
 53         
 54         
 55         if(flag) 
 56             printf("TAK\\n");
 57             if(cnt % 2 == 1)
 58                 for(int i = 0; i < n; i++)
 59                     if(row[i].is == 2)
 60                         for(int j = 0; j < m; j++)
 61                             t = (G[i][j] >> num);
 62                             if(t % 2 == 0)
 63                                 printf("%d", j+1);
 64                                 break;
 65                             
 66                         
 67                     
 68                     else printf("%d", 1);       //1是随便取的，只要在[1,m]内就行
 69                     
 70                     //输出格式
 71                     if(i == n-1) printf("\\n");
 72                     else printf(" ");
 73                 
 74             
 75             else
 76                 int fd = -1;      
 77                 //随便找符合第三种情况的一行，产生贡献
 78                 for(int i = 0; i < n; i++)
 79                     if(row[i].is == 2)      
 80                         fd = i;
 81                         break;
 82                     
 83                 
 84                 
 85                 for(int i = 0; i < n; i++)
 86                     if(row[i].is == 2)
 87                         if(i == fd)
 88                             for(int j = 0; j < m; j++)
 89                                 t = (G[i][j] >> num);
 90                                 if(t % 2 == 1)
 91                                     printf("%d", j+1);
 92                                     break;
 93                                 
 94                                 
 95                         
 96                         else
 97                             for(int j = 0; j < m; j++)
 98                                 t = (G[i][j] >> num);
 99                                 if(t % 2 == 0)
100                                     printf("%d", j+1);
101                                     break;
102                                 
103                             
104                         
105                     
106                     else printf("%d", 1);    //同上
107                     
108                     //输出格式
109                     if(i == n-1) printf("\\n");
110                     else printf(" ");
111                 
112             
113             return 0;
114         
115     
116     
117     printf("NIE\\n");
118     
119     return 0;
120