Fuzzy模糊推导(Matlab实现)
Posted troy-daniel
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Fuzzy模糊推导(Matlab实现)相关的知识,希望对你有一定的参考价值。
问题呈述
在模糊控制这门课程中,学到了与模糊数学及模糊推理相关的内容,但是并不太清楚我们在选择模糊规则时应该如何处理,是所有的规则都需要由人手工选择,还是仅需要选择其中的一部分就可以了。因此,在课程示例的基础上做了如下的探究。
设计一个以E、EC作为输入,U作为输出的模糊推理系统,令E、EC、U的隶属度函数为如下:
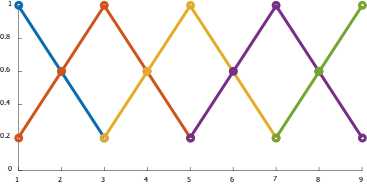
| 1 | 0.6 | 0.2 | 0 | 0 | 0 | 0 | 0 | 0 |
|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.6 | 1 | 0.6 | 0.2 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0.2 | 0.6 | 1 | 0.6 | 0.2 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0.2 | 0.6 | 1 | 0.6 | 0.2 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0.2 | 0.6 | 1 |
分别给定“中心十字规则”以及“最强对角线规则”作为初始规则,观察由此推导出的结果,以验证初始模糊规则库应该如何选择。
结果
中心十字规则
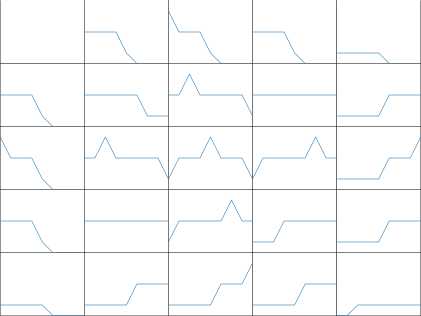
其中,列索引代表E,行索引代表EC,中间的数据区域代表U。1代表负大(NB),2代表负中(NM),3代表零(Z),4代表正中(PB),5代表正大(PB)。
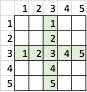
最强对角线

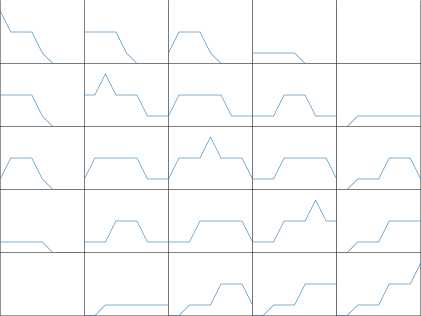
结果分析
从上面的结果可以分析得出:
- 当提供部分规则时,其它规则可由这些规则导出;
- 强对角线规则作为初始规则时,推导效果较好;
- 在强对角线中,左下角和右上角的隶属度为零,这与人的主观判断相同,即“误差正大,但是误差速度为负大,即误差减小(趋于零)的速度最大”,此时不应有主观判断,即维持原态即可。
Additional
tight_subplot.m
function ha = tight_subplot(Nh, Nw, gap, marg_h, marg_w)
% tight_subplot creates "subplot" axes with adjustable gaps and margins
%
% ha = tight_subplot(Nh, Nw, gap, marg_h, marg_w)
%
% in: Nh number of axes in hight (vertical direction)
% Nw number of axes in width (horizontaldirection)
% gap gaps between the axes in normalized units (0...1)
% or [gap_h gap_w] for different gaps in height and width
% marg_h margins in height in normalized units (0...1)
% or [lower upper] for different lower and upper margins
% marg_w margins in width in normalized units (0...1)
% or [left right] for different left and right margins
%
% out: ha array of handles of the axes objects
% starting from upper left corner, going row-wise as in
% going row-wise as in
%
% Example: ha = tight_subplot(3,2,[.01 .03],[.1 .01],[.01 .01])
% for ii = 1:6; axes(ha(ii)); plot(randn(10,ii)); end
% set(ha(1:4),'XTickLabel',''); set(ha,'YTickLabel','')
% Pekka Kumpulainen 20.6.2010 @tut.fi
% Tampere University of Technology / Automation Science and Engineering
if nargin<3; gap = .02; end
if nargin<4 || isempty(marg_h); marg_h = .05; end
if nargin<5; marg_w = .05; end
if numel(gap)==1;
gap = [gap gap];
end
if numel(marg_w)==1;
marg_w = [marg_w marg_w];
end
if numel(marg_h)==1;
marg_h = [marg_h marg_h];
end
axh = (1-sum(marg_h)-(Nh-1)*gap(1))/Nh;
axw = (1-sum(marg_w)-(Nw-1)*gap(2))/Nw;
py = 1-marg_h(2)-axh;
ha = zeros(Nh*Nw,1);
ii = 0;
for ih = 1:Nh
px = marg_w(1);
for ix = 1:Nw
ii = ii+1;
ha(ii) = axes('Units','normalized', ...
'Position',[px py axw axh], ...
'XTickLabel','', ...
'YTickLabel','');
px = px+axw+gap(2);
end
py = py-axh-gap(1);
end中心十字规则
clc;
E = [1,0.6,0,0,0,0,0,0,0;0.2,0.6,1,0.6,0.2,0,0,0,0;0,0,0.2,0.6,1,0.6,0.2,0,0;0,0,0,0,0.2,0.6,1,0.6,0.2;0,0,0,0,0,0,0.2,0.6,1];
EC = E;
U = E;
% ----------------------------------------------------------------------------------
% Calculate R
% Deduct relationship
% ----------------------------------------------------------------------------------
R = zeros(81,9);
for i = 1:5
A = E(i,:)';
B = EC(3,:);
C = U(i,:);
AB = min(repmat(A,1,9), repmat(B,9,1));
AB = reshape(AB, [81,1]);
RC = min(repmat(AB,1,9), repmat(C, 81,1));
R = max(R,RC);
end
for i = [1,2,4,5]
A = E(3,:)';
B = EC(i,:);
C = U(i,:);
AB = min(repmat(A,1,9), repmat(B,9,1));
AB = reshape(AB, [81,1]);
RC = min(repmat(AB,1,9), repmat(C, 81,1));
R = max(R,RC);
end
% ----------------------------------------------------------------------------------
% Calculate C
% Relationship induction
% ----------------------------------------------------------------------------------
C = zeros(9,5,5);
for i = 1:5
for j = 1:5
A = E(i,:)';
B = EC(j,:);
AB = min(repmat(A,1,9), repmat(B,9,1));
AB = reshape(AB, [81,1]);
C(:,i,j) = max(min(repmat(AB, 1, 9), R));
end
end
% ----------------------------------------------------------------------------------
% Plot
% ----------------------------------------------------------------------------------
figure(2);clf;
x = (1:9)/9;
ha = tight_subplot(5,5,[.0 .0],[.0 .0],[.0 .0]);
for i = 1:5
for j = 1:5
axes(ha(i*5-5+j));
h = plot(x, C(:,i,j));
ylim([0,1.2]);
xlim([min(x), max(x)]);
set(gca,'XTick',[])
set(gca,'YTick',[])
end
end最强对角线规则
clc;
E = [1,0.6,0,0,0,0,0,0,0;0.2,0.6,1,0.6,0.2,0,0,0,0;0,0,0.2,0.6,1,0.6,0.2,0,0;0,0,0,0,0.2,0.6,1,0.6,0.2;0,0,0,0,0,0,0.2,0.6,1];
EC = E;
U = E;
% ----------------------------------------------------------------------------------
% Calculate R
% Deduct relationship
% ----------------------------------------------------------------------------------
R = zeros(81,9);
for i = 1:5
A = E(i,:)';
B = EC(i,:);
C = U(i,:);
AB = min(repmat(A,1,9), repmat(B,9,1));
AB = reshape(AB, [81,1]);
RC = min(repmat(AB,1,9), repmat(C, 81,1));
R = max(R,RC);
end
% ----------------------------------------------------------------------------------
% Calculate C
% Relationship induction
% ----------------------------------------------------------------------------------
C = zeros(9,5,5);
for i = 1:5
for j = 1:5
A = E(i,:)';
B = EC(j,:);
AB = min(repmat(A,1,9), repmat(B,9,1));
AB = reshape(AB, [81,1]);
C(:,i,j) = max(min(repmat(AB, 1, 9), R));
end
end
% ----------------------------------------------------------------------------------
% Plot
% ----------------------------------------------------------------------------------
figure(2);clf;
x = (1:9)/9;
ha = tight_subplot(5,5,[.0 .0],[.0 .0],[.0 .0]);
for i = 1:5
for j = 1:5
axes(ha(i*5-5+j));
h = plot(x, C(:,i,j));
ylim([0,1.2]);
xlim([min(x), max(x)]);
set(gca,'XTick',[])
set(gca,'YTick',[])
end
end模糊合成的定义
设\\(P\\)是\\(U\\times V\\) 上的模糊关系,\\(Q\\)是\\(V\\times W\\)上的模糊关系,则\\(R\\)是\\(U\\times W\\)上的模糊关系,它是\\(P\\circ Q\\)的合成,其隶属函数被定义为
\\[
\\mu_R\\left(u,w\\right)\\Leftrightarrow\\mu_P,Q\\left(u,w\\right)=\\vee_v\\in V\\left\\ \\mu_P\\left(u,v\\right)\\wedge\\mu_Q\\left(v,w\\right)\\right\\
\\]
若式中牌子\\(\\wedge\\)代表“取小–\\(\\min\\)”,\\(\\vee\\)代表“取大–\\(\\max\\)”,这种合成关系即为最大值\\(\\cdot\\)最小值合成,合成关系\\(R=P\\circ Q\\)。
示例:
\\[
A=\\beginbmatrix0.4 & 0.5 & 0.6\\0.1 & 0.2 & 0.3
\\endbmatrix,B=\\beginbmatrix0.1 & 0.2\\0.3 & 0.4\\0.5 & 0.6
\\endbmatrix.
\\]
则\\(A\\circ B=\\beginbmatrix0.5 & 0.6\\\\ 0.3 & 0.3 \\endbmatrix\\), \\(B\\circ A=\\beginbmatrix0.1 & 0.2 & 0.2\\\\ 0.3 & 0.3 & 0.3\\\\ 0.4 & 0.5 & 0.5 \\endbmatrix\\)。
有定义为
\\[
A\\times B = A^\\mathrmT\\circ B.
\\]
模糊推导示例
已知一个双输入单输出的模糊系统,其输入量为\\(x\\)和\\(y\\),输出量为\\(z\\),其输入输出的关系可用如下两条模糊规则描述:
\\(R_1\\):如果\\(x\\)是\\(A_1\\) and \\(y\\)是\\(B_1\\),则\\(z\\)是\\(C_1\\)
\\(R_2\\):如果\\(x\\)是\\(A_2\\) and \\(y\\)是\\(B_2\\),则\\(z\\)是\\(C_2\\)
$$
\\beginarrayccc
A_1=\\frac1a_1+\\frac0.5a_2+\\frac0a_3 & B_1=\\frac1b_1+\\frac0.6b_2+\\frac0.2b_3 & C_1=\\frac1c_1+\\frac0.4c_2+\\frac0c_3\\
A_2=\\frac0a_1+\\frac0.5a_2+\\frac1a_3 & B_2=\\frac0.2b_1+\\frac0.6b_2+\\frac1b_3 & C_2=\\frac0c_1+\\frac0.4c_2+\\frac1c_3
\\endarray
$$
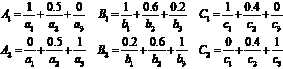
(感觉被恶心到了,不知道为什么这儿的array环境始终出不来)
现已知输入\\(x\\)为\\(A'\\), \\(y\\)为\\(B’\\),试求输出量。
$$
\\beginarraycc
A‘=\\frac0.5a_1+\\frac1a_2+\\frac0.5a_3
& B‘=\\frac0.6b_1+\\frac1b_2+\\frac0.6b_3\\
\\endarray
$$
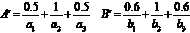
\\[ \\beginaligned A_1\\timesB_1 & =A_1^T\\circB_1=\\left[\\beginarrayccc 1 & 0.5 & 0\\endarray\\right]^T\\left[\\beginarrayccc 1 & 0.6 & 0.2\\endarray\\right]\\ & =\\left[\\beginarrayccc 1 & 0.6 & 0.2\\0.5 & 0.5 & 0.2\\0 & 0 & 0 \\endarray\\right] \\endaligned \\]
将其按行展开得(把矩阵压扁为一行向量)
\\[
R_1=\\barR_A_1\\timesB_1^T\\wedgeC_1=\\left[\\beginarrayc
1\\0.6\\0.2\\0.5\\0.5\\0.2\\0\\0\\0
\\endarray\\right]\\wedge\\left[\\beginarrayccc
1 & 0.4 & 0\\endarray\\right]=\\left[\\beginarrayccc
1 & 0.4 & 0\\1 & 0.4 & 0\\0.2 & 0.2 & 0\\0.5 & 0.4 & 0\\0.5 & 0.4 & 0\\0.2 & 0.2 & 0\\0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0
\\endarray\\right]
\\]
同理:
\\[
R_2=\\barR_A_2\\timesB_2^T\\wedgeC_2=\\left[\\beginarrayccc
0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\\0 & 0.2 & 0.2\\0 & 0.4 & 0.5\\0 & 0.4 & 0.5\\0 & 0.2 & 0.2\\0 & 0.4 & 0.6\\0 & 0.4 & 1
\\endarray\\right]
\\]
总的蕴含关系为
\\[
R=R_1\\cupR_2=\\left[\\beginarrayccc
1 & 0.4 & 0\\0.6 & 0.4 & 0\\0.2 & 0.2 & 0\\0.5 & 0.4 & 0.2\\0.5 & 0.4 & 0.5\\0.2 & 0.4 & 0.5\\0 & 0.2 & 0.2\\0 & 0.4 & 0.6\\0 & 0.4 & 1
\\endarray\\right]
\\]
计算输入量的模糊集合
\\[
A'\\text and B'=A'\\times B'=\\left[\\beginarrayc
0.5\\1\\0.5
\\endarray\\right]\\wedge\\left[\\beginarrayccc
0.6 & 1 & 0.6\\endarray\\right]=\\left[\\beginarrayccc
0.5 & 0.5 & 0.5\\0.6 & 1 & 0.6\\0.5 & 0.5 & 0.5
\\endarray\\right]
\\]
\\[
\\barR_A'\\times B'^T=\\left[\\beginarrayccccccccc
0.5 & 0.5 & 0.5 & 0.6 & 1 & 0.6 & 0.5 & 0.5 & 0.5\\endarray\\right]
\\]
\\[
C'=\\barR_A'\\times B'\\circ R=\\left[\\beginarrayccc
0.5 & 0.4 & 0.5\\endarray\\right]
\\]
\\[
C'=\\frac0.5c_1+\\frac0.4c_2+\\frac0.5c_3
\\]
以上是关于Fuzzy模糊推导(Matlab实现)的主要内容,如果未能解决你的问题,请参考以下文章
ElasticSearch05_模糊匹配背景fuzzy核心参数说明编写JAVA代码实现纠错