第七章小结_查找

Posted 2021-12-16 luoyang0515

查找

一些定义

召回率和准确率

因为PTA上的题目会涉及，所以在这里提一下
参考：精度评定中的准确率（Precision）和召回率（Recall），怎样量化评价搜索引擎的结果质量
当进行查找的时候，样本会被分成两类，在这里举例：苹果和非苹果
那么进行检索的时候，就会出现四种情况：

1. 苹果被认为是苹果
2. 不是苹果被认为是苹果
3. 苹果被认为是非苹果
4. 不是苹果被认为是非苹果

召回率(Recall) = 系统检索到的相关文件 / 系统所有相关的文件总数
准确率(Precision) = 系统检索到的相关文件 / 系统所有检索到的文件总数
假如分类器只将苹果特征十分明显、是苹果的概率非常高的样本分为苹果，其余的样本分为非苹果，此时该分类器的准确率就会非常的高，但是它因为将所有疑似苹果都错误分为非苹果，召回率变得非常低。
假如分类器将所有可能为苹果的样本全部划分为苹果，其余的样本为非苹果，此时该分类器的召回率会非常之高，但是它因为将所有可能为苹果的样本分为苹果时引入了许多错误，准确率不高。
召回率衡量一个查询搜索到所有相关文档的能力，而准确率（Precision）衡量搜索系统排除不相关文档的能力。
通俗来说，召回率表示所有靠谱的结果中，有多少被你给找回来了；准确率就是算一算你查询得到的结果中有多少是靠谱的

平均查找长度

参考：在哈希表中查找成功和不成功时的平均查找长度如何计算？
传说中的ASL（Average Search Length），分为查找成功的ASL（ASLsucc）和和查找失败的ASL（ASLunsucc），下面的例子都以查找概率相等为前提

查找成功的平均查找长度（ASLsucc）

其实就是在构造散列表的时候，把所有关键字的比较次数加起来求平均值，假设有以下散列表：7，8，30，11，18，9，14 根据H(key) = (3*key) MOD 7放入长度为10的散列表中，用线性探测处理冲突
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 关键字 | 7 | 14 | 9 | 8 | | 11 | 30 | 18 | | |
| 比较次数 | 1 | 2 | 1 | 1 | | 1 | 1 | 3 | | |
ASLsucc=（1+2+1+1+1+1+3）/7=10/7

查找失败的平均查找长度（ASLunsucc）

计算查找不成功的次数就直接找关键字到第一个地址上关键字为空的距离即可，因为不管经过计算得到的下标是什么，通过线性探测，只要遇到第一个空位前都没找到，那就是找不到了。
不同于ASLsucc，ASLunsucc不是针对关键字的比较次数，而是所有关键存放的位置到空着的位置的距离。由于我们是通过MOD 7的来的下标，所以需要比较的下标为0-6即可，所有也是0-6下标到空位的距离相加
要注意的是这里的距离实际上指的是从该位置开始到空位的比较次数，我们从下标0开始看
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 关键字 | 7 | 14 | 9 | 8 | | 11 | 30 | 18 | | |
| 到空位的距离 | 5 | 4 | 3 | 2 | 1 | 4 | 3 | | | |
下标0到第一个空位置（下标4）要比较5次才能确定不存在，因此距离为5，以此类推。到下标6时，比较到下一个空位置（下标8）要经过3次比较，比较完后结束比较。
ASLunsucc=（5+4+3+2+1+4+3）/7=22/7
注意：ASLsucc的分母由关键字的个数决定，而ASLunsucc的分母由初次计算所得结果的个数决定（比如MOD 7，会有0-6七个结果），上面相等是个巧合...

概念总结

这一章有很多方法，为了避免搞混（因为已经搞混了）所以在这里试着罗列一下

线性表查找

1. 顺序查找：遍历呗
2. 二分查找（折半查找）：二分搜索啦，每次取中位数。要求数据本身按一定顺序排列
3. 分块查找（索引顺序查找）：需要额外建立一个索引表存储块的信息。要求索引表按关键字有序，块内不一定有序但块和块之间必须有序（比如第二块中所有关键字都大于第一块的最大关键字）

树表查找

1. 二叉排序树（二叉查找树）：左边<根<右边，递归就是了。由于二叉排序数根据输入数据顺序不同能产生不同的树，而不同树显然查找速度不同，高度越小，查找越快。为了得到高度尽可能小的树，所以有了2
2. 平衡二叉树（AVL树）：引入平衡因子（左右子树深度之差，只能为±1，0）。只要有一个结点的平衡因子大于1，则二叉树不平衡。但当数据量很大的时候，仍要反复进行内外存交换，很耗时。
3. B-树：不再是二叉树，而是多叉树，从而实现一层有多个关键字，有效减少高度，得以存储庞大数据量，避免内外存反复的交换，如磁盘的目录管理，书记库的索引组织。但是不能进行范围查找。因为我自己不怎么清楚所以讲的详细一点XD（参考：B-树的详解）
   
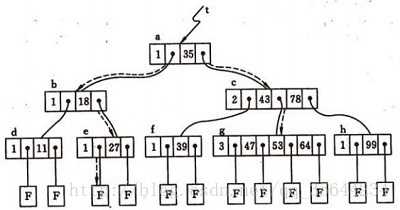
   每个结点显示有个数字表示这之后有几个关键字，然后每个关键字有左右两个指针分别指向小于和大于这个关键字的子树。最下面的F表示失败节点，实际为空。
   如上图所示，这是我们的一个4阶的B-树，现在假设我们需要查找45这个数是否在B-树中：
   从根节点出发，发现根节点a有1个关键字为35，其中45>35，往右子树走，进入节点c
   发现结点c有2个关键字，其中其中43<45<78,所以进入结点g
   发现结点g有3个关键字，其中3<45<47,所以继续往下走，发现进入了结束符结点：F，所以45不在B-树中
   
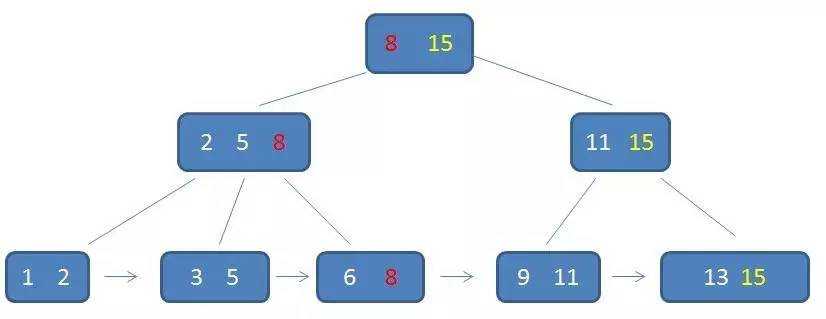
4. B+树：类似B树，它的相邻叶子结点用指针连在一起，形成有序链表；并且每一个父结点的元素都出现在子节点中，是子节点的最大/最小元素。
   参考：b+树图文详解
   相比B-树，B+树每次查询最终都到叶子结点，而B-树只要找到匹配元素就可以了，不管是叶子结点还是中间结点。也就是说，B-树每个结点的关键字后都带有自己的记录；而B+树除了叶子结点带有记录外，其余结点都只有向下的指针。这使得B+树一个结点能存储更多的关键字。
   B+树最大的优势就是范围查找，这由叶子节点形成的链表实现。比如查找范围3-11的数，我们可以先通过查找最小的3，再沿着链表向下搜索，直到11。
   

散列表查找

散列表查找法/哈希查找，主要是散列表的构建和冲突的解决

构造方法

1. 数字分析法：分析关键字，选择差别比较大的当做地址（下标），比如学号。适合事先知道关键字的数字分布情况
2. 平方取中法：把关键字平方后取中间几位作为地址。适合不了解关键字所有情况或每一位都有某些数字重复出现
3. 折叠法：分为移位叠加和边界叠加。先把较长的数据进行分割（比如三位一割），移位叠加就是把每个三位数加起来，取结果的后三位。边界叠加就是在移位叠加的基础上，把一些数据反过来写。适合关键字位数比较多，散列地址位数比较少，且不好用1和2的情况
   比如453，877，652，13，移位叠加的结果是453+877+652+13=[1]995；边界叠加的结果是453+778+652+31=[1]914，其中把877反过来写成778，13反过来写成31。
   
4. 除留余数法：H(key)=key%p。最常用，一般p取小于表长的最大质数。

解决冲突

分为开放地址法和链地址法

开发地址法

1. 线性探测法：将散列表循环，一旦冲突就往下放
2. 二次探测法：发生冲突是，放到后1，前1，后4，前4，后9......的位置。相比线性探测法，这种方法能让关键字分布更平均，减小之后出现冲突的概率

3. 伪随机探测法：利用随机数来进行冲突时位置的选择。创建时需要记录随机数生成的顺序，用以之后查找

   链地址法

   类似邻接表，将所有冲突的地址以链式存储的形式放在相应位置的后面。

   个人目标

   上次学习小结匆匆忙忙赶出来的，感觉效果不理想，所以还是要认真总结。
   这次因为有很多概念，所以参考了很多其他博客，感觉效果不错。很多人能把复杂的概念讲的很具体，会举例子，配图，很容易理解。
   虽然上次的总结比较草率，但之后还是有去补上代码啦，多敲代码还是有好处的。不过还是希望能匀出更多的时间看一些文字，比如STL，比如高质量编程指南。