5月赛总结

Posted 2021-12-09 mch5201314

首先还是有很多东西没学好，其实看了题解之后就知道怎么做了。
我去我怎么这么辣鸡？学不好，混子，不做点难题，是没有进步的。
第一题
就是给你四个数字看是否可以通过四则运算得到24

分析

这种明显就是暴力，可是我当时就觉得分类讨论太多。自己没有信心去做。
其实你想最后得到24的方式就是两个数的加减乘除之一。那你就暴力把每种运算和每种排列全部
枚举就完了，注意的是除法必须是整除求分母不为0，我怀疑我不会递归。递归可以省很多代码量。而且不容易出错。
辣鸡死了

代码

#include<bits/stdc++.h>
using namespace std;
int a[4];
bool flag=0;
void fun(int pre,int la,int cur){
    if(flag) return;
    if(cur==3){
        if(pre+la==24||pre-la==24||pre*la==24)
        flag=1;
        if(la!=0&&pre%la==0&&pre/la==24)
        flag=1;
        return;
    }
    fun(pre+la,a[cur+1],cur+1);
    fun(pre-la,a[cur+1],cur+1);
    fun(pre*la,a[cur+1],cur+1);
    if(la!=0&&pre%la==0)
    fun(pre/la,a[cur+1],cur+1);
     
    fun(pre,la+a[cur+1],cur+1);
    fun(pre,la-a[cur+1],cur+1);
    fun(pre,la*a[cur+1],cur+1);
    if(a[cur+1]!=0&&la%a[cur+1]==0)
    fun(pre,la/a[cur+1],cur+1);
}
int main(){
    flag=0;
    for(int i=0;i<4;i++)
    scanf("%d",&a[i]);
    sort(a,a+4);
    do{
        fun(a[0],a[1],1);
    }while(next_permutation(a,a+4)&&!flag);
    if(flag) puts("Yes");
    else puts("No");
    return 0;
}

第二题
现在有两种操作： 第一种操作对[l,r]区间内每幢房子塞入一个皮卡丘; 第二种操作对第l次到第r次的操作重复一遍。
问依次进行m次操作后每幢房子内皮卡丘的个数。数据保证l < r 且对于第二种操作所给区间一定是之前的操作,对于第一种操作r一定<=n。
初始房子为空。
问你最后每个房子的数量。

分析

这我刚开始想用线段树维护这个东西，发现难度很大，根本不行。后来我想到了用差分。但是后面的操作，会把前面的操作给重复。我不知道怎么处理这个东西。
最后题解是差分，不过需要两个差分。一个维护第i次操作进行了几次，一个维护某个位置加了多少次。然后操作的差分要从后面开始，因为后面会包含前面的操作
这题你需要两个差分，而且方向还相反，属实是个好题。后面在遇到不会就砍头。气死了。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=1e9+7;
const int N=1e5+10;
ll a[N],b[N];
struct str{
    int op,l,r;
}d[N];
int main(){
    int T,n,m;
    scanf("%d",&T);
    while(T--){
        memset(a,0,sizeof(a));
        memset(b,0,sizeof(b));
        scanf("%d%d",&n,&m);
        b[m+1]++;
        b[0]--;
        for(int i=1;i<=m;i++)
        scanf("%d%d%d",&d[i].op,&d[i].l,&d[i].r);
        for(int i=m;i>0;i--){
            b[i]=(b[i]+b[i+1])%mod;
            if(d[i].op==2){
                int l=d[i].l,r=d[i].r;
                b[r]=(b[r]+b[i])%mod;
                b[l-1]=(b[l-1]-b[i]+mod)%mod;
            }
            else{
                int l=d[i].l,r=d[i].r;
                a[l]=(a[l]+b[i])%mod;
                a[r+1]=(a[r+1]-b[i]+mod)%mod;
            }
        }
        for(int i=1;i<=n;i++){
            a[i]=(a[i-1]+a[i])%mod;
            if(i!=n) printf("%lld ",a[i]);
            else printf("%lld\\n",a[i]);
        }
    }
    return 0;
}

第七题
就是个快速幂，不过这个地方取模1e12，快速幂会超过long long.我是意识到这个问题，可是后面的时间都没有解决办法。
后来看别人的，在快速幂哪里用了 __int128 就可以了。这个是long long的两倍。这个东西我没用过，这次知道了
正解是快速幂+乘法优化，变成1e6进制的数
我没搞懂，得补了。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=1e12;
ll fp(ll x,ll y){
    __int128 ans=1;
    __int128 ba=x%mod;
    while(y){
        if(y&1) ans=ans*ba%mod;
        ba=(ba*ba)%mod;
        y>>=1;
    }
    return ans;
}
int main(){
   long double a,b,c;
   ll d,n;
   int q;
   scanf("%Lf%Lf%Lf",&a,&b,&c);
   ll x,y,z,p,t;
   x=(ll)(a); t=(ll)(b); p=(ll)(c);
   /*1.9 2.1 2.2
   1
   100000000000000000 100000000000000000*/
   if(b-t>0) y=t+1ll;
   else y=t;
   z=c+0.5;
   scanf("%d",&q);
   while(q--){
    scanf("%lld%lld",&d,&n);
    ll ba=fp(d,n);
    ll ans=(x%mod+y%mod+z%mod+ba)%mod;
    printf("%lld\\n",ans);
   }
    return 0;
}

第九题
题目描述
作为acm集训队一员的你，有一天拿到了你的历史训练时长记录表。你当然是想让你的训练时长看起来好看一些，所以你想调整这份记录表，使得训练时长最少的一天的时间在所有可能的调整方案中最大。你还有m分钟就梦醒了，时间紧迫，你每一分钟可以使得连续的w天时长记录多一个单位时间。注意，在梦中，你不需要考虑一天有多少的时间限制。 输出经过你的调整，最小的时长。(睡醒前的答案)

输入
多组数据，第一行为一个整数T，表示数据组数（T<=10) 接下来每组数据，开头为n，m，w（1<=w , n<=100000, 0<=m <= 1000000),表示有记录的历史训练天数 接下来一行n个数，表示这一天你的签到时长t（0<=t<=1000000）

输出
输出T行，每行代表一组的答案。

分析

二分啊，不过加了一个技巧而已，自己不会弄。就是差分检查。发现这次考这个差分，这确实是个好东西啊。
二分最低哪个，check是否可以在m次以内做到。如果当前小于check值就进行那么多次加，同时往右的连续w个都加，所以用差分标记。
这没想到就是平时没有做这方面的，用的少，不知道这种套路。该死，多刷题啊老哥。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+10;
const int M=2e6+10;
int add[N],a[N];
int n,m,w;
bool ok(int k){
    memset(add,0,sizeof(add));
    int res=m;
    for(int i=1;i<=n;i++)
    {
        add[i]+=add[i-1];
        int h=k-a[i]-add[i];
        if(h>0)
        {
            res-=h;
            add[i]+=h;
            add[i+w]-=h;
        }
    }
    return res>=0?1:0; 
}
int main(){
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        cin>>n>>m>>w;
        for(int i=1;i<=n;i++)
        cin>>a[i];
        int l=0,r=M;
        int ans;
        while(l<=r){
            int mid=(l+r)>>1;
            if(ok(mid)){
                ans=mid;
                l=mid+1;
            }
            else r=mid-1;
        }
        cout<<ans<<endl;
    }
    return 0;
}

第十题
题目描述
有一个只包含1和2的序列，试翻转一个区间，使得结果中非递减子序列最长。输出翻转后数列中非递减子序列的最长长度。

输入
第一行为数据组数T，每组数据包含两行，第一行为序列的长度，第二行为n个数，表示数列中的数。(T <=6 && n <= 2e5)

输出
每组数据输出一行，表示答案。
这题是个dp,就是没想到。刷题太少了。不会套路。
其实就是找出最长的1111222211112222，我们可以开dp[4]，分别表示以红色标出的值为结尾的最长子序列。
因为这样中间哪个22221111反转才是最多的。果然是做题太少了
转移公式

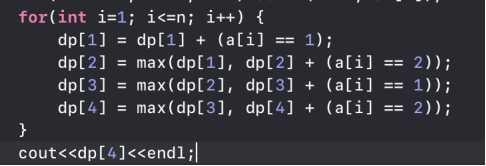
代码

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
int dp[5],s[N];
int main(){
    int t,n;
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin>>t;
    while(t--){
        cin>>n;
        for(int i=1;i<=n;i++)
        cin>>s[i];
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=n;i++){
            dp[1]=dp[1]+(s[i]==1);
            dp[2]=max(dp[2]+(s[i]==2),dp[1]);
            dp[3]=max(dp[3]+(s[i]==1),dp[2]);
            dp[4]=max(dp[4]+(s[i]==2),dp[3]);
        }
        cout<<dp[4]<<endl;
    }
    return 0;
}

后面的题用到后缀数组，我还不会，哪个东西可以解决很多字符串的问题
很厉害的。要学啊
总结就是做题少了，sb一个