数据结构丨队列和栈
Posted vincent1997
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构丨队列和栈相关的知识,希望对你有一定的参考价值。
队列
先入先出的数据结构
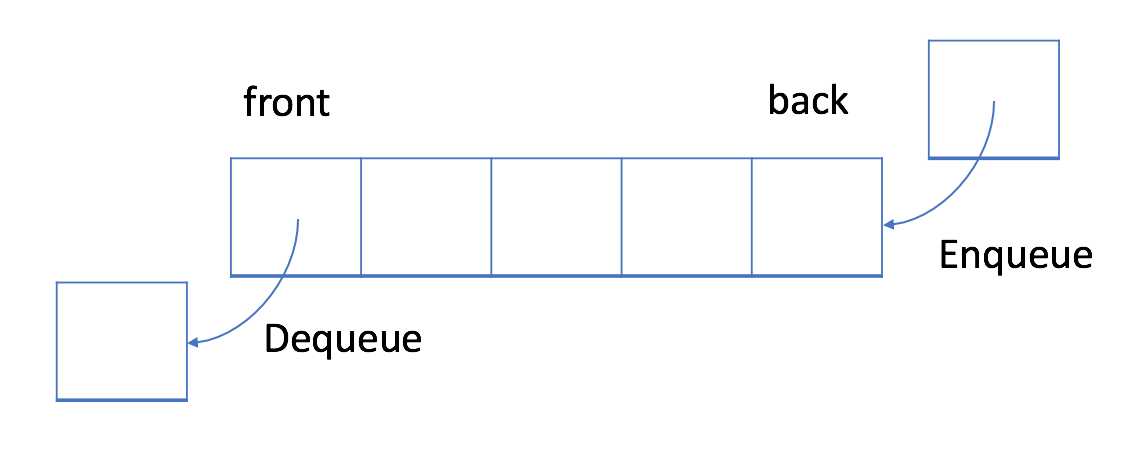
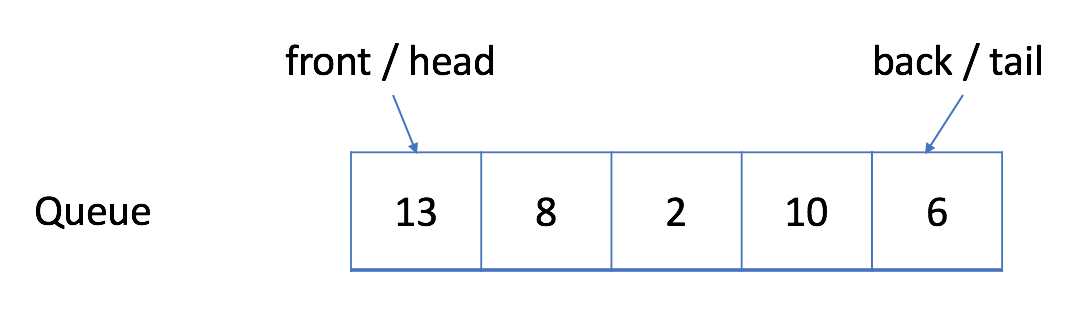
在 FIFO 数据结构中,将首先处理添加到队列中的第一个元素。
如上图所示,队列是典型的 FIFO 数据结构。插入(insert)操作也称作入队(enqueue),新元素始终被添加在队列的末尾。 删除(delete)操作也被称为出队(dequeue)。 你只能移除第一个元素。
示例 - 队列
- 入队:您可以单击下面的
Enqueue以查看如何将新元素 6 添加到队列中。
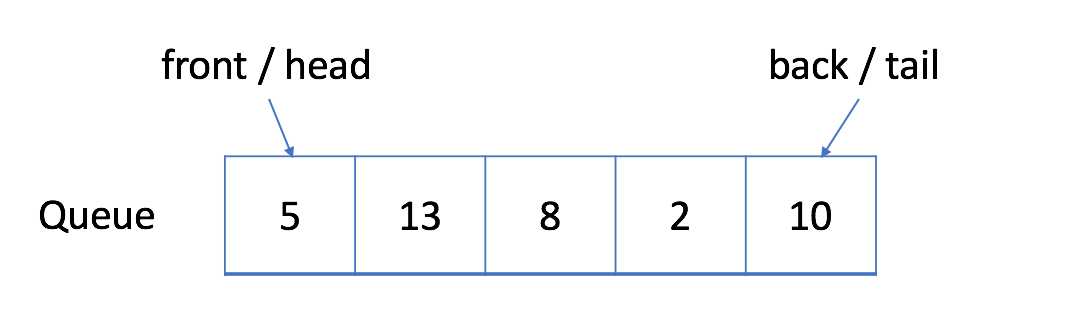
?
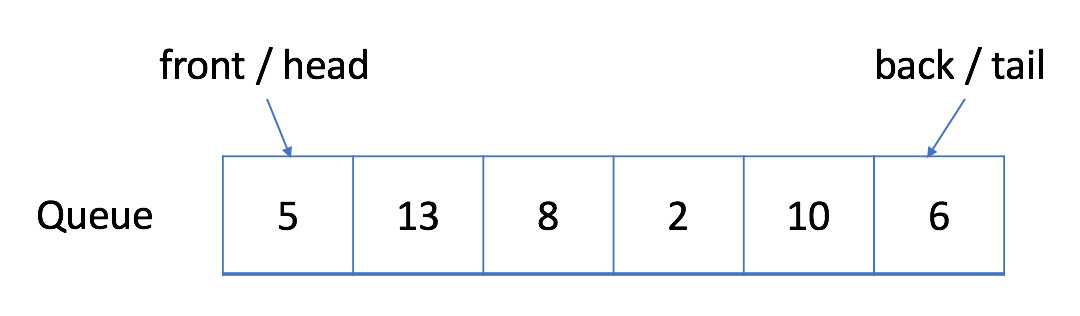
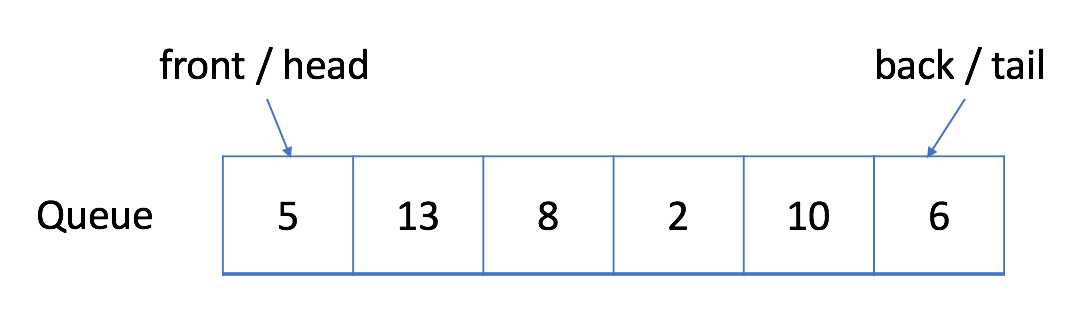
- 出队:您可以单击下面的
Dequeue以查看将删除哪个元素。
队列-实现
为了实现队列,我们可以使用动态数组和指向队列头部的索引。
如上所述,队列应支持两种操作:入队和出队。入队会向队列追加一个新元素,而出队会删除第一个元素。 所以我们需要一个索引来指出起点。
这是一个供你参考的实现:
#include <iostream>
#include <vector>
using namespace std;
class MyQueue {
private:
// store elements
vector<int> data;
// a pointer to indicate the start position
int p_start;
public:
MyQueue() {p_start = 0;}
/** Insert an element into the queue. Return true if the operation is successful. */
bool enQueue(int x) {
data.push_back(x);
return true;
}
/** Delete an element from the queue. Return true if the operation is successful. */
bool deQueue() {
if (isEmpty()) {
return false;
}
p_start++;
return true;
};
/** Get the front item from the queue. */
int Front() {
return data[p_start];
};
/** Checks whether the queue is empty or not. */
bool isEmpty() {
return p_start >= data.size();
}
};
int main() {
MyQueue q;
q.enQueue(5);
q.enQueue(3);
if (!q.isEmpty()) {
cout << q.Front() << endl;
}
q.deQueue();
if (!q.isEmpty()) {
cout << q.Front() << endl;
}
q.deQueue();
if (!q.isEmpty()) {
cout << q.Front() << endl;
}
}缺点
上面的实现很简单,但在某些情况下效率很低。 随着起始指针的移动,浪费了越来越多的空间。 当我们有空间限制时,这将是难以接受的。

让我们考虑一种情况,即我们只能分配一个最大长度为 5 的数组。当我们只添加少于 5 个元素时,我们的解决方案很有效。 例如,如果我们只调用入队函数四次后还想要将元素 10 入队,那么我们可以成功。
但是我们不能接受更多的入队请求,这是合理的,因为现在队列已经满了。但是如果我们将一个元素出队呢?

实际上,在这种情况下,我们应该能够再接受一个元素。
循环队列
此前,我们提供了一种简单但低效的队列实现。
更有效的方法是使用循环队列。 具体来说,我们可以使用固定大小的数组和两个指针来指示起始位置和结束位置。 目的是重用我们之前提到的被浪费的存储。
让我们通过一个示例来查看循环队列的工作原理。 你应该注意我们入队或出队元素时使用的策略。

仔细检查动画,找出我们用来检查队列是空还是满的策略。
下一个练习,我们将让你自己尝试实现循环队列,之后会提供给你一个解决方案。
设计循环队列
设计你的循环队列实现。 循环队列是一种线性数据结构,其操作表现基于 FIFO(先进先出)原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。
循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里,一旦一个队列满了,我们就不能插入下一个元素,即使在队列前面仍有空间。但是使用循环队列,我们能使用这些空间去存储新的值。
你的实现应该支持如下操作:
MyCircularQueue(k): 构造器,设置队列长度为 k 。Front: 从队首获取元素。如果队列为空,返回 -1 。Rear: 获取队尾元素。如果队列为空,返回 -1 。enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。isEmpty(): 检查循环队列是否为空。isFull(): 检查循环队列是否已满。
示例:
MyCircularQueue circularQueue = new MycircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1); // 返回 true
circularQueue.enQueue(2); // 返回 true
circularQueue.enQueue(3); // 返回 true
circularQueue.enQueue(4); // 返回 false,队列已满
circularQueue.Rear(); // 返回 3
circularQueue.isFull(); // 返回 true
circularQueue.deQueue(); // 返回 true
circularQueue.enQueue(4); // 返回 true
circularQueue.Rear(); // 返回 4
提示:
- 所有的值都在 0 至 1000 的范围内;
- 操作数将在 1 至 1000 的范围内;
- 请不要使用内置的队列库。
#include <iostream>
#include <vector>
using namespace std;
/// One more space implementation
/// Time Complexity: O(1)
/// Space Complexity: O(n)
class MyCircularQueue
{
private:
int front, tail;
vector<int> data;
public:
MyCircularQueue(int k)
{
front = tail = 0;
data.clear();
for (int i = 0; i <= k; i++) //这里多分配了一个空间
data.push_back(-1);
}
bool enQueue(int value)
{
if (isFull())
return false;
data[tail] = value;
tail = (tail + 1) % data.size();
return true;
}
bool deQueue()
{
if (isEmpty())
return false;
front = (front + 1) % data.size();
return true;
}
int Front(){
if(isEmpty())
return -1;
return data[front];
}
int Rear()
{
if (isEmpty())
return -1;
int index = tail - 1;
if (index < 0)
index += data.size();
return data[index];
}
bool isEmpty()
{
return front == tail;
}
bool isFull()
{
return (tail + 1) % data.size() == front;
}
};循环队列-实现
在循环队列中,我们使用一个数组和两个指针(head 和 tail)。 head 表示队列的起始位置,tail 表示队列的结束位置。
这里我们提供了代码供你参考:
class MyCircularQueue {
private:
vector<int> data;
int head;
int tail;
int size;
public:
/** Initialize your data structure here. Set the size of the queue to be k. */
MyCircularQueue(int k) {
data.resize(k);
head = -1;
tail = -1;
size = k;
}
/** Insert an element into the circular queue. Return true if the operation is successful. */
bool enQueue(int value) {
if (isFull()) {
return false;
}
if (isEmpty()) {
head = 0; //第一次入队,下标将从0开始。
}
tail = (tail + 1) % size; //之后只需调整队尾指针。
data[tail] = value;
return true;
}
/** Delete an element from the circular queue. Return true if the operation is successful. */
bool deQueue() {
if (isEmpty()) {
return false;
}
if (head == tail) { //这里与下面的判断方式不同
head = -1;
tail = -1;
return true;
}
head = (head + 1) % size;
return true;
}
/** Get the front item from the queue. */
int Front() {
if (isEmpty()) {
return -1;
}
return data[head];
}
/** Get the last item from the queue. */
int Rear() {
if (isEmpty()) {
return -1;
}
return data[tail];
}
/** Checks whether the circular queue is empty or not. */
bool isEmpty() {
return head == -1; //这不是用head == tail判断
}
/** Checks whether the circular queue is full or not. */
bool isFull() {
return ((tail + 1) % size) == head;
}
};
/**
* Your MyCircularQueue object will be instantiated and called as such:
* MyCircularQueue obj = new MyCircularQueue(k);
* bool param_1 = obj.enQueue(value);
* bool param_2 = obj.deQueue();
* int param_3 = obj.Front();
* int param_4 = obj.Rear();
* bool param_5 = obj.isEmpty();
* bool param_6 = obj.isFull();
*/队列-用法
大多数流行语言都提供内置的队列库,因此您无需重新发明轮子。
如前所述,队列有两个重要的操作,入队 enqueue 和出队 dequeue。 此外,我们应该能够获得队列中的第一个元素,因为应该首先处理它。
下面是使用内置队列库及其常见操作的一些示例:
#include <iostream>
int main() {
// 1. Initialize a queue.
queue<int> q;
// 2. Push new element.
q.push(5);
q.push(13);
q.push(8);
q.push(6);
// 3. Check if queue is empty.
if (q.empty()) {
cout << "Queue is empty!" << endl;
return 0;
}
// 4. Pop an element.
q.pop();
// 5. Get the first element.
cout << "The first element is: " << q.front() << endl;
// 6. Get the last element.
cout << "The last element is: " << q.back() << endl;
// 7. Get the size of the queue.
cout << "The size is: " << q.size() << endl;
}我们在本文之后提供了练习,以帮助你熟悉这些操作。请记住,当你想要按顺序处理元素时,使用队列可能是一个很好的选择。
数据流中的移动平均值
*到了这一题,发现要开会员才能看到题目-_-b,于是我就去百度找题目了。*
Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.
For example,
MovingAverage m = new MovingAverage(3);
m.next(1) = 1
m.next(10) = (1 + 10) / 2
m.next(3) = (1 + 10 + 3) / 3
m.next(5) = (10 + 3 + 5) / 3
给一个整数流和一个窗口,计算在给定大小的窗口里的数字的平均值。
解法:队列queue,用一个queue记录进入窗口的整数。当流进窗口的整数不足时,计算所有窗口内的数字和返回,当进入窗口的整数多于窗口大小时,移除最先进入窗口的整数,新的整数进入queue,然后计算窗口内的整数和。#include <iostream>
#include <queue>
using namespace std;
/// Using Queue
/// Time Complexity: O(1)
/// Space Complexity: O(size)
class MovingAverage
{
private:
queue<int> q;
int sz, sum;
public:
MovingAverage(int size)
{
sz = size;
sum = 0;
}
double next(int val)
{
if (q.size() == sz)
{
sum -= q.front();
q.pop();
}
sum += val;
q.push(val);
return (double)sum / q.size();
}
}队列和广度优先搜索
队列和BFS
广度优先搜索(BFS)的一个常见应用是找出从根结点到目标结点的最短路径。在本文中,我们提供了一个示例来解释在 BFS 算法中是如何逐步应用队列的。
示例
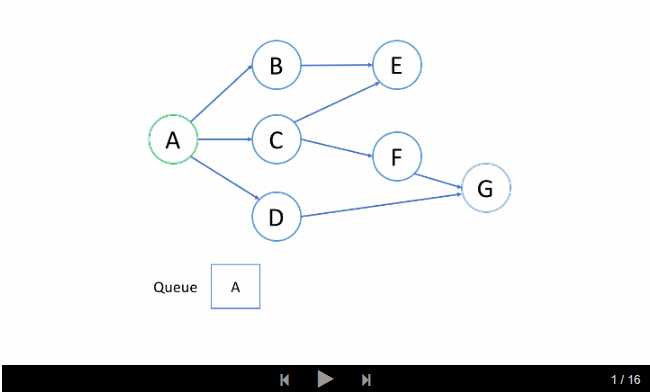
这里我们提供一个示例来说明如何使用 BFS 来找出根结点 A 和目标结点 G 之间的最短路径。
洞悉
观看上面的动画后,让我们回答以下问题:
1. 结点的处理顺序是什么?
在第一轮中,我们处理根结点。在第二轮中,我们处理根结点旁边的结点;在第三轮中,我们处理距根结点两步的结点;等等等等。
与树的层序遍历类似,越是接近根结点的结点将越早地遍历。
如果在第 k 轮中将结点 X 添加到队列中,则根结点与 X 之间的最短路径的长度恰好是 k。也就是说,第一次找到目标结点时,你已经处于最短路径中。
2. 队列的入队和出队顺序是什么?
如上面的动画所示,我们首先将根结点排入队列。然后在每一轮中,我们逐个处理已经在队列中的结点,并将所有邻居添加到队列中。值得注意的是,新添加的节点不会立即遍历,而是在下一轮中处理。
结点的处理顺序与它们添加到队列的顺序是完全相同的顺序,即先进先出(FIFO)。这就是我们在 BFS 中使用队列的原因。
广度优先搜索-模板
之前,我们已经介绍了使用 BFS 的两个主要方案:遍历或找出最短路径。通常,这发生在树或图中。正如我们在章节描述中提到的,BFS 也可以用于更抽象的场景中。
在本文中,我们将为你提供一个模板。然后,我们在本文后提供一些习题供你练习。
在特定问题中执行 BFS 之前确定结点和边缘非常重要。通常,结点将是实际结点或是状态,而边缘将是实际边缘或可能的转换。
模板I
在这里,我们为你提供伪代码作为模板:
/**
* Return the length of the shortest path between root and target node.
*/
int BFS(Node root, Node target) {
Queue<Node> queue; // store all nodes which are waiting to be processed
int step = 0; // number of steps neeeded from root to current node
// initialize
add root to queue;
// BFS
while (queue is not empty) {
step = step + 1;
// iterate the nodes which are already in the queue
int size = queue.size();
for (int i = 0; i < size; ++i) {
Node cur = the first node in queue;
return step if cur is target;
for (Node next : the neighbors of cur) {
add next to queue;
}
remove the first node from queue;
}
}
return -1; // there is no path from root to target
}- 如代码所示,在每一轮中,队列中的结点是
等待处理的结点。 - 在每个更外一层的
while循环之后,我们距离根结点更远一步。变量step指示从根结点到我们正在访问的当前结点的距离。
模板 II
有时,确保我们永远不会访问一个结点两次很重要。否则,我们可能陷入无限循环。如果是这样,我们可以在上面的代码中添加一个哈希集来解决这个问题。这是修改后的伪代码:
/**
* Return the length of the shortest path between root and target node.
*/
int BFS(Node root, Node target) {
Queue<Node> queue; // store all nodes which are waiting to be processed
Set<Node> used; // store all the used nodes
int step = 0; // number of steps neeeded from root to current node
// initialize
add root to queue;
add root to used;
// BFS
while (queue is not empty) {
step = step + 1;
// iterate the nodes which are already in the queue
int size = queue.size();
for (int i = 0; i < size; ++i) {
Node cur = the first node in queue;
return step if cur is target;
for (Node next : the neighbors of cur) {
if (next is not in used) {
add next to queue;
add next to used;
}
}
remove the first node from queue;
}
}
return -1; // there is no path from root to target
}有两种情况你不需要使用哈希集:
- 你完全确定没有循环,例如,在树遍历中;
- 你确实希望多次将结点添加到队列中。
墙与门
You are given a m x n 2D grid initialized with these three possible values.
-1- A wall or an obstacle.0- A gate.INF- Infinity means an empty room. We use the value231 - 1 = 2147483647to representINFas you may assume that the distance to a gate is less than2147483647.
Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF.
For example, given the 2D grid:
INF -1 0 INF
INF INF INF -1
INF -1 INF -1
0 -1 INF INFAfter running your function, the 2D grid should be:
3 -1 0 1
2 2 1 -1
1 -1 2 -1
0 -1 3 4这道题类似一种迷宫问题,规定了-1表示墙,0表示门,让求每个点到门的最近的曼哈顿距离,这其实类似于求距离场Distance Map的问题,那么我们先考虑用DFS来解,思路是,我们搜索0的位置,每找到一个0,以其周围四个相邻点为起点,开始DFS遍历,并带入深度值1,如果遇到的值大于当前深度值,我们将位置值赋为当前深度值,并对当前点的四个相邻点开始DFS遍历,注意此时深度值需要加1,这样遍历完成后,所有的位置就被正确地更新了,参见代码如下:
解法一:
class Solution {
public:
void wallsAndGates(vector<vector<int>>& rooms) {
for (int i = 0; i < rooms.size(); ++i) {
for (int j = 0; j < rooms[i].size(); ++j) {
if (rooms[i][j] == 0) dfs(rooms, i, j, 0);
}
}
}
void dfs(vector<vector<int>>& rooms, int i, int j, int val) {
if (i < 0 || i >= rooms.size() || j < 0 || j >= rooms[i].size() || rooms[i][j] < val) return;
rooms[i][j] = val;
dfs(rooms, i + 1, j, val + 1);
dfs(rooms, i - 1, j, val + 1);
dfs(rooms, i, j + 1, val + 1);
dfs(rooms, i, j - 1, val + 1);
}
};那么下面我们再来看BFS的解法,需要借助queue,我们首先把门的位置都排入queue中,然后开始循环,对于门位置的四个相邻点,我们判断其是否在矩阵范围内,并且位置值是否大于上一位置的值加1,如果满足这些条件,我们将当前位置赋为上一位置加1,并将次位置排入queue中,这样等queue中的元素遍历完了,所有位置的值就被正确地更新了,参见代码如下:
解法二:
class Solution {
public:
void wallsAndGates(vector<vector<int>>& rooms) {
queue<pair<int, int>> q;
vector<vector<int>> dirs{{0, -1}, {-1, 0}, {0, 1}, {1, 0}};
for (int i = 0; i < rooms.size(); ++i) {
for (int j = 0; j < rooms[i].size(); ++j) {
if (rooms[i][j] == 0) q.push({i, j});
}
}
while (!q.empty()) {
int i = q.front().first, j = q.front().second; q.pop();
for (int k = 0; k < dirs.size(); ++k) {
int x = i + dirs[k][0], y = j + dirs[k][1];
if (x < 0 || x >= rooms.size() || y < 0 || y >= rooms[0].size() || rooms[x][y] < rooms[i][j] + 1) continue;
rooms[x][y] = rooms[i][j] + 1;
q.push({x, y});
}
}
}
};岛屿数量
给定一个由 ‘1‘(陆地)和 ‘0‘(水)组成的的二维网格,计算岛屿的数量。一个岛被水包围,并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围。
示例 1:
输入:
11110
11010
11000
00000
输出: 1示例 2:
输入:
11000
11000
00100
00011
输出: 3思路:只需判断陆地有没有跟已发现的岛屿相邻,如果没有相邻,则是新的岛屿。
/// Source : https://leetcode.com/problems/number-of-islands/description/
/// Author : liuyubobobo
/// Time : 2018-08-25
#include <iostream>
#include <vector>
#include <cassert>
#include <queue>
using namespace std;
/// Floodfill - BFS
/// Time Complexity: O(n*m)
/// Space Complexity: O(n*m)
class Solution {
private:
int d[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}}; //分别表示上、右、下、左
int m, n;
public:
int numIslands(vector<vector<char>>& grid) {
m = grid.size();
if(m == 0)
return 0;
n = grid[0].size();
if(n == 0)
return 0;
vector<vector<bool>> visited(m, vector<bool>(n, false));
int res = 0;
for(int i = 0 ; i < m ; i ++)
for(int j = 0 ; j < n ; j ++)
if(grid[i][j] == '1' && !visited[i][j]){
bfs(grid, i, j, visited);
res ++;
}
return res;
}
private:
void bfs(vector<vector<char>>& grid, int x, int y, vector<vector<bool>>& visited){
queue<pair<int, int>> q;
q.push(make_pair(x, y));
visited[x][y] = true;
while(!q.empty()){
int curx = q.front().first;
int cury = q.front().second;
q.pop();
for(int i = 0; i < 4; i ++){
int newX = curx + d[i][0];
int newY = cury + d[i][1];
if(inArea(newX, newY) && !visited[newX][newY] && grid[newX][newY] == '1'){
q.push(make_pair(newX, newY));
visited[newX][newY] = true;
}
}
}
return;
}
bool inArea(int x, int y){
return x >= 0 && x < m && y >= 0 && y < n;
}
};
int main() {
vector<vector<char>> grid1 = {
{'1','1','1','1','0'},
{'1','1','0','1','0'},
{'1','1','0','0','0'},
{'0','0','0','0','0'}
};
cout << Solution().numIslands(grid1) << endl;
// 1
// ---
vector<vector<char>> grid2 = {
{'1','1','0','0','0'},
{'1','1','0','0','0'},
{'0','0','1','0','0'},
{'0','0','0','1','1'}
};
cout << Solution().numIslands(grid2) << endl;
// 3
return 0;
}打开转盘锁
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: ‘0‘, ‘1‘, ‘2‘, ‘3‘, ‘4‘, ‘5‘, ‘6‘, ‘7‘, ‘8‘, ‘9‘ 。每个拨轮可以自由旋转:例如把 ‘9‘ 变为 ‘0‘,‘0‘ 变为 ‘9‘ 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 ‘0000‘ ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出最小的旋转次数,如果无论如何不能解锁,返回 -1。
示例 1:
输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出:6
解释:
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的,
因为当拨动到 "0102" 时这个锁就会被锁定。示例 2:
输入: deadends = ["8888"], target = "0009"
输出:1
解释:
把最后一位反向旋转一次即可 "0000" -> "0009"。示例 3:
输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出:-1
解释:
无法旋转到目标数字且不被锁定。示例 4:
输入: deadends = ["0000"], target = "8888"
输出:-1提示:
- 死亡列表
deadends的长度范围为[1, 500]。 - 目标数字
target不会在deadends之中。 - 每个
deadends和target中的字符串的数字会在 10,000 个可能的情况‘0000‘到‘9999‘中产生。
思路:等价于八领域的迷宫问题,并绕过死锁区域。字符和数字的转换通过加 ‘0‘ 实现。
/// Source : https://leetcode.com/problems/open-the-lock/description/
/// Author : liuyubobobo
/// Time : 2017-12-23
#include <iostream>
#include <vector>
#include <set>
#include <queue>
#include <cassert>
using namespace std;
/// BFS
/// Time Complexity: O(charset^N)
/// Space Complexity: O(charset^N)
class Solution {
public:
int openLock(vector<string>& deadends, string target) {
set<string> dead;
for(string s: deadends)
dead.insert(s);
if(dead.find(target) != dead.end() || dead.find("0000") != dead.end())
return -1;
set<string> visited;
queue<pair<string, int>> q;
q.push(make_pair("0000", 0));
visited.insert("0000");
while(!q.empty()){
string cur = q.front().first;
int step = q.front().second;
q.pop();
vector<string> next = getNext(cur, dead);
for(string next_s: next)
if(visited.find(next_s) == visited.end()){
if(next_s == target)
return step + 1;
visited.insert(next_s);
q.push(make_pair(next_s, step + 1));
}
}
return -1;
}
private:
vector<string> getNext(const string& s, const set<string>& dead){
vector<string> res;
assert(s.size() == 4);
for(int i = 0 ; i < 4 ; i ++){
int num = s[i] - '0';
int d = num + 1;
if(d > 9) d = 0;
string t = s;
t[i] = ('0' + d);
if(dead.find(t) == dead.end())
res.push_back(t);
d = num - 1;
if(d < 0) d = 9;
t = s;
t[i] = ('0' + d);
if(dead.find(t) == dead.end())
res.push_back(t);
}
return res;
}
};
int main() {
vector<string> dead1 = {"0201","0101","0102","1212","2002"};
string target1 = "0202";
cout << Solution().openLock(dead1, target1) << endl;
vector<string> dead2 = {"8888"};
string target2 = "0009";
cout << Solution().openLock(dead2, target2) << endl;
vector<string> dead3 = {"8887","8889","8878","8898","8788","8988","7888","9888"};
string target3 = "8888";
cout << Solution().openLock(dead3, target3) << endl;
vector<string> dead4 = {"1002","1220","0122","0112","0121"};
string target4 = "1200";
cout << Solution().openLock(dead4, target4) << endl;
return 0;
}完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.示例 2:
输入: n = 13
输出: 2
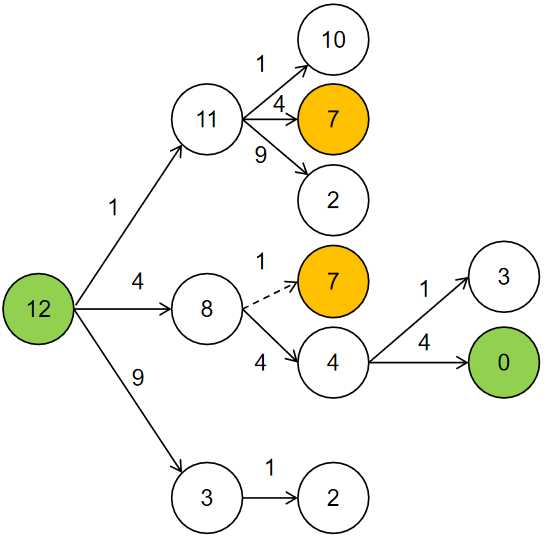
解释: 13 = 4 + 9.思路:该问题可转化为求图的无权最短路径,即正整数n到0间是否存在一条最短路径,路径上节点数目最少。因此采用BFS,率先抵达0的路径即为所求。此外,重复出现的节点,可不加入图中。如下图中第一个7若能到达0,则之后再出现的7也能抵达0,并且第一次出现的7所历经的层数一定比之后的7要少,无需重复计算。
/// Source : https://leetcode.com/problems/perfect-squares/description/
/// Author : liuyubobobo
/// Time : 2017-11-17
#include <iostream>
#include <vector>
#include <queue>
#include <stdexcept>
using namespace std;
/// BFS
/// Time Complexity: O(n)
/// Space Complexity: O(n)
class Solution {
public:
int numSquares(int n) {
if(n == 0)
return 0;
queue<pair<int, int>> q;
q.push(make_pair(n, 0));
vector<bool> visited(n + 1, false);
visited[n] = true;
while(!q.empty()){
int num = q.front().first;
int step = q.front().second;
q.pop();
for(int i = 1; num - i * i >= 0; i ++){
int a = num - i * i;
if(!visited[a]){
if(a == 0) return step + 1;
q.push(make_pair(a, step + 1));
visited[a] = true;
}
}
}
throw invalid_argument("No Solution.");
}
};
int main() {
cout << Solution().numSquares(12) << endl;
cout << Solution().numSquares(13) << endl;
return 0;
}以上是关于数据结构丨队列和栈的主要内容,如果未能解决你的问题,请参考以下文章