图——图的Kruskal法最小生成树实现
Posted 子宇24
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了图——图的Kruskal法最小生成树实现相关的知识,希望对你有一定的参考价值。
1,最小生成树的特征:
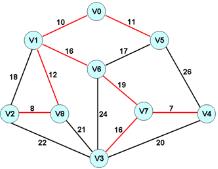
1,选取的边是图中权值较小的边;
2,所有边连接后不构成回路;
2,prim 算法是以顶点为核心的,最下生成树最大的特征是边,但 prim 算法非要以顶点为核心来进行,有些复杂和难以理解;
3,既然最小生成树关心的是如何选择 n - 1 条边,那么是否可以直接以边为核心进行算法设计?
4,简单尝试:

1,由 4 个顶点构成的图,选择 3 条权值最小的边;
2,还要设法避免回路;
5,需要解决的问题:

1,如何判断新选择的边与已选择的边是否构成回路?
6,技巧:前驱标记数组(避开新加入边造成回路问题)
1,定义数组:Array<int> p(vCount());
2,定义数组元素的意义:
1,p[n] 表示顶点 n 在边的连接通路上的另一端顶点;
3,前驱标记数组究竟是怎么来的?
7,最小生成树算法的核心步骤(Kruskal):
1,定义前驱标记数组:Array<int> p(vCount());
2,获取当前图中的所有边,并存储于 edges 数组中;
3,对数组 deges 按照权值进行排序;
4,利用 p 数组在 edges 数组中选择前 n - 1 不构成回路的边;
8,Kruskal 算法流程:
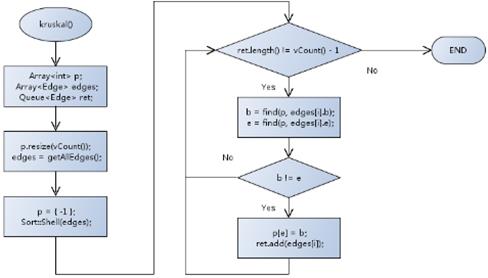
9,关键的 find 查找函数:

10,最小生成树算法 Kruskal (克鲁斯卡)实现:
1 /* 最小、大生成树的 kruskal 算法 */ 2 SharedPointer< Array< Edge<E> > > kruskal(const bool MINMUM = true) 3 { 4 LinkQueue< Edge<E> > ret; // 返回的队列 5 SharedPointer< Array< Edge<E> > > edges = getUndirectedEdges(); // 将无相图中的所有边都拿到 6 DynamicArray<int> p(vCount()); // 前驱标记数组 7 8 /* 设置前驱标记值 */ 9 for(int i=0; i<p.length(); i++) 10 { 11 p[i] = -1; 12 } 13 14 /* 对边数组排序 */ 15 Sort::Shell(*edges, MINMUM); // 第二个参数对边进行从大到小的次序排序,用来生成最大生成树 16 17 /* 进入循环,挑选边 */ 18 for(int i=0; (i<edges->length()) && (ret.length() < (vCount()-1)); i++) // 最多循环边的个数次,且如果边很多但已经有 N - 1 条边被选择了,那么结束循环 19 { 20 int b = find(p, (*edges)[i].b); // 在前驱标记数组中查找挑选的边的两个顶点 21 int e = find(p, (*edges)[i].e); // 前驱标记数组用于判断新选择的边是否会造成回路 22 23 if( b != e) // 相等会构成回路 24 { 25 p[e] = b; // 修改前驱标记数组 26 27 ret.add((*edges)[i]); // 将这条边加入结果集合中去 28 } 29 } 30 31 if( ret.length() != (vCount()-1) ) // 判断边是否够,不够就不能构成最小生成树 32 { 33 THROW_EXCEPTION(InvalidOperationException, "No enough edges for Kruskal operation ..."); 34 } 35 36 return toArray(ret); // 将结果转换为数组 37 }
11,Kruskal 算法测试代码:
1 #include <iostream> 2 #include "MatrixGraph.h" 3 #include "ListGraph.h" 4 5 using namespace std; 6 using namespace DTLib; 7 8 template< typename V, typename E > 9 Graph<V, E>& GraphEasy() 10 { 11 static MatrixGraph<4, V, E> g; 12 13 g.setEdge(0, 1, 1); 14 g.setEdge(1, 0, 1); 15 g.setEdge(0, 2, 3); 16 g.setEdge(2, 0, 3); 17 g.setEdge(1, 2, 1); 18 g.setEdge(2, 1, 1); 19 g.setEdge(1, 3, 4); 20 g.setEdge(3, 1, 4); 21 g.setEdge(2, 3, 1); 22 g.setEdge(3, 2, 1); 23 24 return g; 25 } 26 27 template< typename V, typename E > 28 Graph<V, E>& GraphComplex() 29 { 30 static ListGraph<V, E> g(9); 31 32 g.setEdge(0, 1, 10); 33 g.setEdge(1, 0, 10); 34 g.setEdge(0, 5, 11); 35 g.setEdge(5, 0, 11); 36 g.setEdge(1, 2, 18); 37 g.setEdge(2, 1, 18); 38 g.setEdge(1, 8, 12); 39 g.setEdge(8, 1, 12); 40 g.setEdge(1, 6, 16); 41 g.setEdge(6, 1, 16); 42 g.setEdge(2, 3, 22); 43 g.setEdge(3, 2, 22); 44 g.setEdge(2, 8, 8); 45 g.setEdge(8, 2, 8); 46 g.setEdge(3, 8, 21); 47 g.setEdge(8, 3, 21); 48 g.setEdge(3, 6, 24); 49 g.setEdge(6, 3, 24); 50 g.setEdge(3, 7, 16); 51 g.setEdge(7, 3, 16); 52 g.setEdge(3, 4, 20); 53 g.setEdge(4, 3, 20); 54 g.setEdge(4, 5, 26); 55 g.setEdge(5, 4, 26); 56 g.setEdge(4, 7, 7); 57 g.setEdge(7, 4, 7); 58 g.setEdge(5, 6, 17); 59 g.setEdge(6, 5, 17); 60 g.setEdge(6, 7, 19); 61 g.setEdge(7, 6, 19); 62 63 return g; 64 } 65 66 int main() 67 { 68 Graph<int, int>& g = GraphEasy<int, int>(); 69 SharedPointer< Array< Edge<int> > > sa = g.kruskal(65535); 70 71 int w = 0; 72 73 for(int i=0; i<sa->length(); i++) 74 { 75 w += (*sa)[i].data; 76 77 cout << (*sa)[i].b << " " << (*sa)[i].e << " " << (*sa)[i].data << endl; 78 } 79 80 cout << "Weight: " << w << endl; 81 82 return 0; 83 }
13,小结:
1,Prim 算法以顶点为核心寻找最小生成树,不够直接;
2,Kruskal 算法以边为核心寻找最小生成树,直观简单;
3,Kruskal 算法中的关键是前驱标记数组的使用;
4,前驱标记数组用于判断新选择的边是否会造成回路;
以上是关于图——图的Kruskal法最小生成树实现的主要内容,如果未能解决你的问题,请参考以下文章