线性代数基础
Posted weizz
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了线性代数基础相关的知识,希望对你有一定的参考价值。
向量
一个向量是一列数。这些数是有序排列的。通过次序中的做因,我们可以确定每个单独的数。
若固定向量的起点,如记之为原点,则向量由其终点唯一确定于是我们可以等同:
1.n维空间中的点;
2.n元有序数组;
3.n维空间中由原点出发的向量;
记向量:
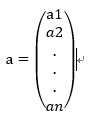
线性空间
组成元素的n维向量,且对加减和标量乘法封闭。
矩阵范数
矩阵范数用来衡量矩阵的大小
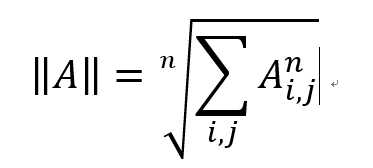
特征分解
存在矩阵A,其中A为n×n方阵,则有:
Ax = λx
其中λ为特征值,x为λ对应的特征向量。
奇异值分解SVD
奇异值分解是将矩阵分解为奇异向量(singular vector)和奇异值(singular value),通过分解有更广泛的应用。每个实数矩阵都有一个奇异值分解,但不一定有特征分解。
假设A为实数矩阵,则有;
A = UDV
若A为一个m×n的矩阵,那么U是一个m×m的矩阵,D是一个n×n的矩阵。
可以把奇异值分解看成线性变换的分解,即将变换分解为 旋转->缩放->旋转
Moore-Penrose 伪逆
对m×n的矩阵A,定义其伪逆(pseudoinverse)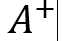 ,使得当A为n阶可逆方阵时,有
,使得当A为n阶可逆方阵时,有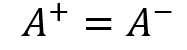 。
。
∈
以上是关于线性代数基础的主要内容,如果未能解决你的问题,请参考以下文章