图——图的Floyd法最短路径实现

Posted 2021-12-07 dishengandziyu

1，Dijkstra 算法一次性求得起始顶点到所有其它顶点的最短路径，如果想要求解任意两个顶点之间的最短路径，可将图中顶点作为起始顶点执行 n 次 Dijkstra 算法就可以了；

  

2，可能解决方案：

      

       1，算法执行结束后，i 到 j 最短路径值存储于 dist[i][j] 中。最短路径前驱结点存储于 path[N][N] 中；

       2，这种方法比较土；

      

3，问题的提法：

       1，已知一个各边权值均大于 0 的带权有向图，对每一对顶点 vi != vj，求出 vi 与 vj 之间的最短路径值以及最短路径上的顶点；

         

4，Floyd 算法核心：

       1，定义一个 n 阶方阵序列：

             

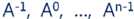
          其中：

           

       2，怀疑当前两个顶点间路径不是最短路径，因此 Floyd 算法尝试通过其他顶点中转、直到找到一个中转点的中转路径最短；

         

5，n 阶方阵中元素的意义：

     

       1，都是由邻接方阵中的权值推得的；

       2，此算法是通过递推的方式得到两个顶点间最短路径的；

       3，把所有的顶点的中转路径都推导完了，也就得到最小路径了；

       4，后面方阵的推导，包含着前面方阵的信息，且每次推导都是最小，直到推导了全部顶点，得到最终最短路径；

      

6，Floyd 算法精髓：

 

 

7，Floyd 算法的实现：

     

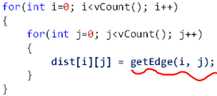
       1，初始化：

              1，本质：使用邻接矩阵初始化 A(-1)；    

       2，A(0), ..., A(n-1) 矩阵推导：

　　　　1，本质：使用中转顶点逐步推导最短路径；

              2，最外层是在说 A(k)矩阵的循环，循环推导完后，得到最短路径矩阵 A(n-1)，即为所求；

                   

 

8，如何记录最短路径上的各个顶点？

       1，定义辅助矩阵：

              1，int path[N][N];  // 路径矩阵

                     1，path[i][j] 表示 i 到 j 的路径上所经过的第 1 个顶点；

                     2，初始化：path[i][j] = -1; or paht[i][j] = j;

                            1，有直接的连接则设置为 j，表示经过的第一个顶点为终值顶点 j；

                            2，没有连接的两个顶点设置为 -1；

                     3，修改：

1 if( (dist[i][k] + dist[k][j]) < dist[i][j]  )
2 {
3      dist[i][j] = dist[i][k] + dist[k][j];
4      path[i][j] = paht[i][k];
5 }

                            1，if 条件为真，由 k 这个顶点中转可以得到一条更短路径，则由 i 到 j 这条路径上所经过的第一个顶点就是由 i 到 k 这条路径上经过的第一个顶点，因为由 k 中转了下；

              2，路径矩阵示例：

　　　　　　1，由一个点的路径推至其它路径：

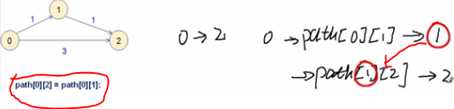
                     2，辅助矩阵和路径：

 

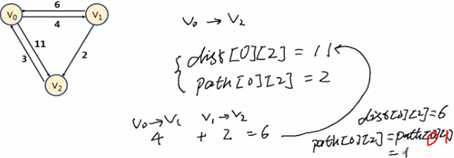
9，Floyd 最短路径算法实现：

 1 　　 /* floyd 每对结点之间最短路径算法，返回值为最短路径；核心为通过中转顶点寻找更短路径 */
 2     SharedPointer< Array<int> > floyd(int x, int y, const E& LIMIT)  // O(n*n*n)
 3     {
 4         LinkQueue<int> ret;
 5 
 6         if( (0 <= x) && (x < vCount()) && (0 <= y) && (y < vCount()) )  //顶点编号要合理
 7         {
 8             DynamicArray< DynamicArray<E> > dist(vCount());  // 定义二维数组，N*N
 9 
10             DynamicArray< DynamicArray<int> > path(vCount());  // 最短路径的辅助数组
11 
12             /* 定义二维数组 */
13             for(int k=0; k<vCount(); k++)
14             {
15                 dist[k].resize(vCount());
16                 path[k].resize(vCount());
17             }
18 
19             /* 初始值设置 */
20             for(int i=0; i<vCount(); i++)
21             {
22                 for(int j=0; j<vCount(); j++)
23                 {
24                     path[i][j] = -1;  // i 和 j 是没有边的
25 
26                     dist[i][j] = isAdjacent(i, j) ? (path[i][j]=j, getEdge(i, j)) : LIMIT;  // 邻接了就设置，利用了逗号表达式，逗号表达式第一个参数是设置顶点，第二个是设置权值
27                 }                                                                           
28             }
29 
30             /* 推导最短路径矩阵 */
31             for(int k=0; k<vCount(); k++)
32             {
33                 for(int i=0; i<vCount(); i++)
34                 {
35                     for(int j=0; j<vCount(); j++)
36                     {   
37                /* 推导规则，用中间顶点中转数据，看是否有最短路径值 */
38                         if( (dist[i][k] + dist[k][j]) < dist[i][j] )
39                         {
40                             dist[i][j] = dist[i][k] + dist[k][j];  // 如果得到最短路径，认为其可能是最短路径，要更新其值
41 
42                             path[i][j] = path[i][k];  // 通过 k 顶点可以找到最小值，则这个顶点找到了
43                          }
44                     }
45                 }
46             }
47 
48             while( (x != -1) && (x != y) )  // 推导到终止顶点为止
49             {
50                 ret.add(x);  // 最短路径上的各个顶点加到返回值中
51 
52                 x = path[x][y];  // 递归的将 path[x][y] 上经过的第一个顶点放入 x 中，然后在下一个递推中从 x 出发再递归处其它顶点；
53             }
54 
55             if( x != -1 )
56             {
57                 ret.add(x);  // 将最后的一个 x 加入返回值队列中，因为上面 x == y，终止了在返回队列中的加入，所以这里要加入
58             }
59         }
60         else
61         {
62             THROW_EXCEPTION(InvalidParameterException, "Index <x, y> is invalid ...");
63         }
64 
65         /* 看看目标的两个最短值之间是否真的有最短路径 */
66         if( ret.length() < 2 )
67         {
68             THROW_EXCEPTION(ArithmeticException, "There is no path from x to y ...");
69         }
70 
71         return toArray(ret);
72     }

 

10，小结：

       1，Floyd 算法通过递推逐步求得所有顶点间的最短路径；

       2，Floyd 算法的本质是通过中转顶点寻找更短的路径；

       3，邻接矩阵是最短路径推导的起始矩阵；

       4，路径矩阵记录了最短路径上的各个顶点；