[转]C#集合类型大揭秘

Posted 2021-12-02 fanqisoft

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了[转]C#集合类型大揭秘相关的知识，希望对你有一定的参考价值。

集合是.NET FCL(Framework Class Library)的重要组成部分，我们平常撸C#代码时免不了和集合打交道，FCL提供了丰富易用的集合类型，给我们撸码提供了极大的便利。正是因为这种与生俱来的便利性，使得我们对集合既熟悉又陌生。很多同学可能一直还是停留在使用的层面上，那么今天我们一起来深入学习一下C#语言中的各种集合。

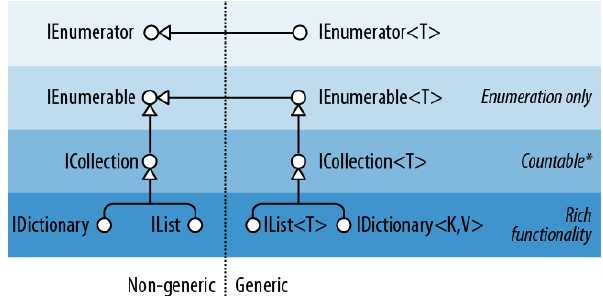
首先我们看一下 FCL 给我们提供的集合接口：

技术图片

FCL提供了泛型和非泛型两大类集合类型。因为非泛型集合装箱和拆箱带来的性能开销问题，和泛型集合相比，已经变得越来越鸡肋。所以我们也侧重于泛型集合的分析，但是两者差别不大。

IEnumerable和IEnumerator

技术图片

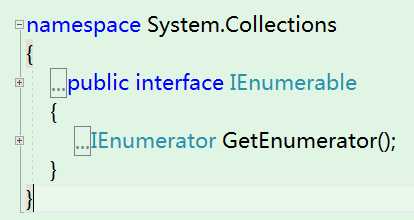
IEnumerable接口是所有集合类型的祖宗接口，其作用相当于Object类型之于其它类型。如果某个类型实现了IEnumerable接口，就意味着它可以被迭代访问，也就可以称之为集合类型（可枚举）。IEnumerable接口定义非常简单，只有一个GetEnumerator()方法用于获取IEnumerator类型的迭代器。

技术图片

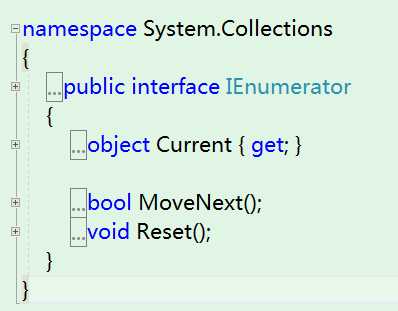
我们可以将迭代器想象成数据库的游标，即序列（集合）中的某个位置，迭代器只能在序列（集合）中向前移动。每调用一次MoveNext()，如果序列（集合）中还有下一个元素，则迭代器移动到下一个元素；Current用于获取序列（集合）中的当前元素；因为迭代器调用一次代码只需要获取一个元素，这意味着我们需要确定访问到了序列（集合）中的哪个位置。Reset()用于重置这种状态，但是基本上不会使用Reset()重置状态。

同一个序列（集合）可能同时存在多个迭代器操作，相当于同时对一个集合进行多个遍历。这种情况下可能会出现迭代彼此交错。那么如何解决呢？

集合类不直接支持 IEnumerator 和
IEnumerator 接口。而是直接支持 IEnumerable接口，其唯一方法是 GetEnumerator，此方法用于返回支持 IEnumerator 的对象。每次调用GetEnumerator()方法时都需要创建一个新的对象，同时迭代器必须保存自身的状态，记录此时已经迭代到哪一个元素。这样迭代器就像是序列中的游标。可以有多个游标，移动其中任何一个都可以枚举集合，与其他迭代器互不影响。

foreach是怎么实现的？

for依赖对 Length 属性和索引运算符 ([]) 的支持。借助 Length 属性，C# 编译器可以使用 for 语句迭代数组中的每个元素。for适用于长度固定且始终支持索引运算符的数组，但并不是所有类型集合的元素数量都是已知的。此外，许多集合类（包括 Stack、Queue 和 Dictionary<TKey ,TValue>）都不支持按索引检索元素。因此，需要使用一种更为通用的方法来迭代元素集合。假设可以确定第一个、第二个和最后一个元素，那么就没有必要知道元素数量，也没有必要支持按索引检索元素。foreach在这种背景下应运而生。实际上，foreach内部使用迭代器的MoveNext和Current完成元素的遍历。

 1 List<int> list = new List<int>();
 2 List<int>.Enumerator enumerator = list.GetEnumerator();
 3 try
 4 {
 5     int number;
 6     while (enumerator.MoveNext())
 7     {
 8         number = enumerator.Current;
 9         Console.WriteLine(number);
10     }
11 }
12 finally
13 {
14     enumerator.Dispose();
15 }

实现自定义集合

我们可以自己实现IEnumerable接口和IEnumerator接口实现自定义集合。

实现自定义可枚举类型：

 1 public class MySet : IEnumerable
 2 {
 3     internal object[] values;
 4 
 5     public MySet(object[] values)
 6     {
 7         this.values = values;
 8     }
 9 
10     public IEnumerator GetEnumerator()
11     {
12         return new MySetIterator(this);
13     }
14 }

手写实现自定义迭代器：

 1 public class MySetIterator : IEnumerator
 2 {
 3     MySet set;
 4     /// <summary>
 5     /// 保存迭代到的位置
 6     /// </summary>
 7     int position;
 8     internal MySetIterator(MySet set)
 9     {
10         this.set = set;
11         position = -1;
12     }
13 
14     public object Current
15     {
16         get
17         {                   
18             if(position==-1||position==set.values.Length)
19             {
20                 throw new   InvalidOperationException();
21              }
22              int index = position;
23              return set.values[index];
24          }
25     }
26 
27     public bool MoveNext()
28     {
29         if(position!=set.values.Length)
30         {
31             position++;
32         }
33         return position < set.values.Length;
34     }
35 
36     public void Reset()
37     {
38         position = -1;
39     }
40 }

测试程序：

1 object[] values = { "a", "b", "c", "d", "e" };
2 MySet mySet = new MySet(values);
3 foreach (var item in mySet)
4 {
5     Console.WriteLine(item);
6 }

这个例子也证明了foreach内部使用迭代器的MoveNext和Current完成遍历。

上面的例子中手写实现迭代器是十分麻烦的，在c#1.0中这是唯一的方式。在c#2.0中，我们可以使用yield语法糖简化迭代器。

1 public IEnumerator GetEnumerator()
2 {
3     for (int i = 0; i < values.Length; i++)
4     {
5         yield return values[i];
6     }
7 }

IEnumerable和IEnumerator虽然实现简单，只有简单的几个成员，但是却支撑起了C#语言中集合这座高楼大厦。

ICollection和ICollection

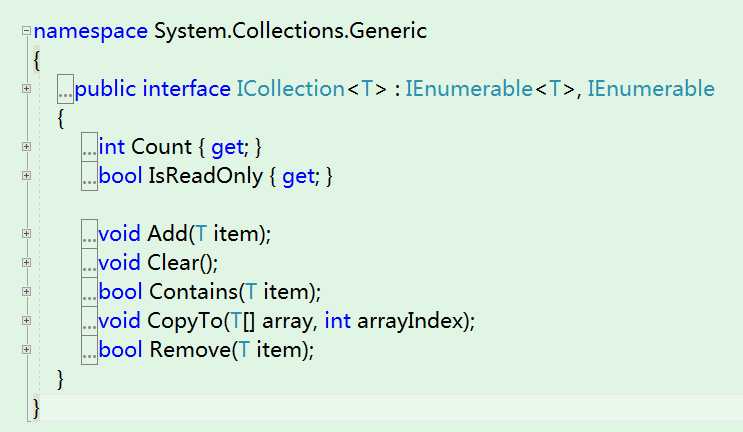
从第一张图中，我们可以得知ICollection继承于IEnumerable接口，并且扩展了IEnumerable接口。

技术图片

主要扩展的功能有：

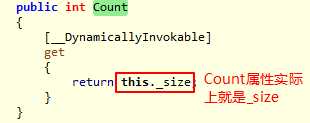
新增了属性Count,用于记录集合元素个数
支持添加元素和移除元素
支持是否包含某元素
支持清空集合等等

对于任何实现了ICollection接口的集合，我们都可以通过第1条Count属性获取当前集合的元素数，所以这些集合也被称为计数集合。

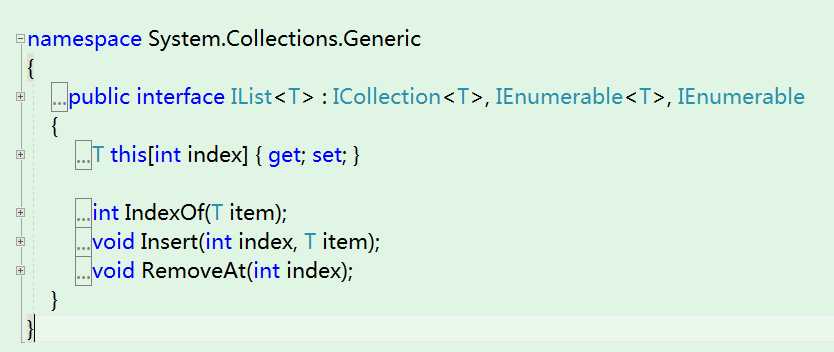
IList 和IList

技术图片

IList接口直接继承于ICollection接口和IEnumerable接口，并且扩展了通过索引操作集合的功能。

主要扩展的功能有：

通过索引获取集合中某个元素
通过元素获取元素在集合中的索引值
通过索引插入元素到集合指定位置
移除集合指定索引处的元素

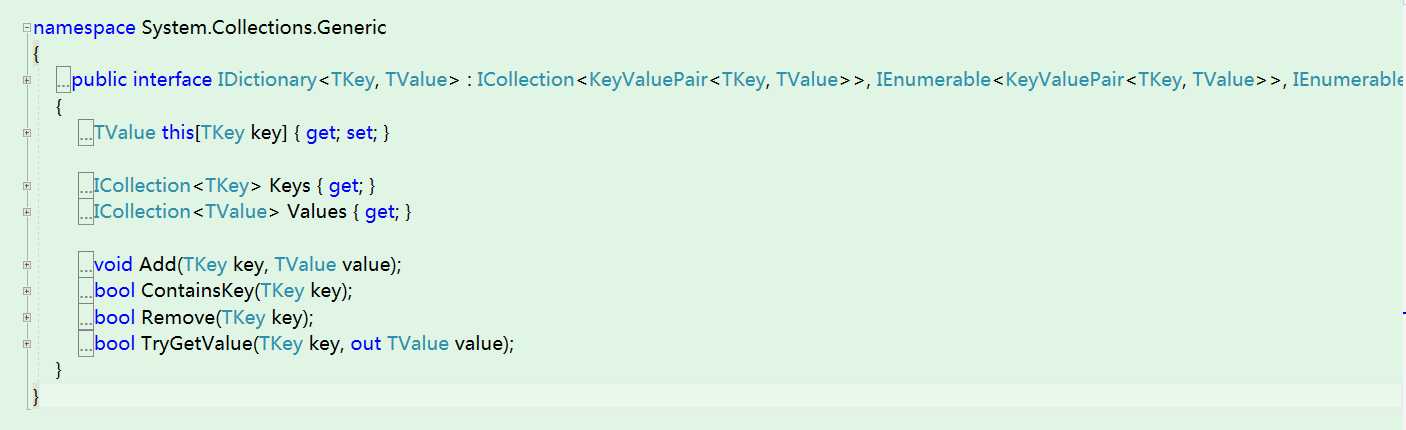
IDictionary<TKey, TValue>和IDictionary

技术图片

IDictionary接口直接继承于ICollection接口和IEnumerable接口，存储的元素是键值对，扩展了通过键操作键值对集合的功能。

主要扩展的功能有：

通过键KEY获取值VALUE
插入新的键值对{KEY:VALUE}
是否包含KEY
通过KEY移除键值对元素

主要的集合的接口介绍完了，下面我们来看一下具体的集合类型。

关联性泛型集合类

1.Dictionary<TKey,TValue>

Dictionary<TKey,TValue>的查询数据所花费的时间是所有集合类里面最快的，因为其内部使用了散列函数加双数组来实现，所以其查询数据操作的时间复杂度可以认为是O（1）。Dictionary<TKey,TValue>的实现是一种典型的牺牲空间换取时间（双数组）的做法。

技术图片

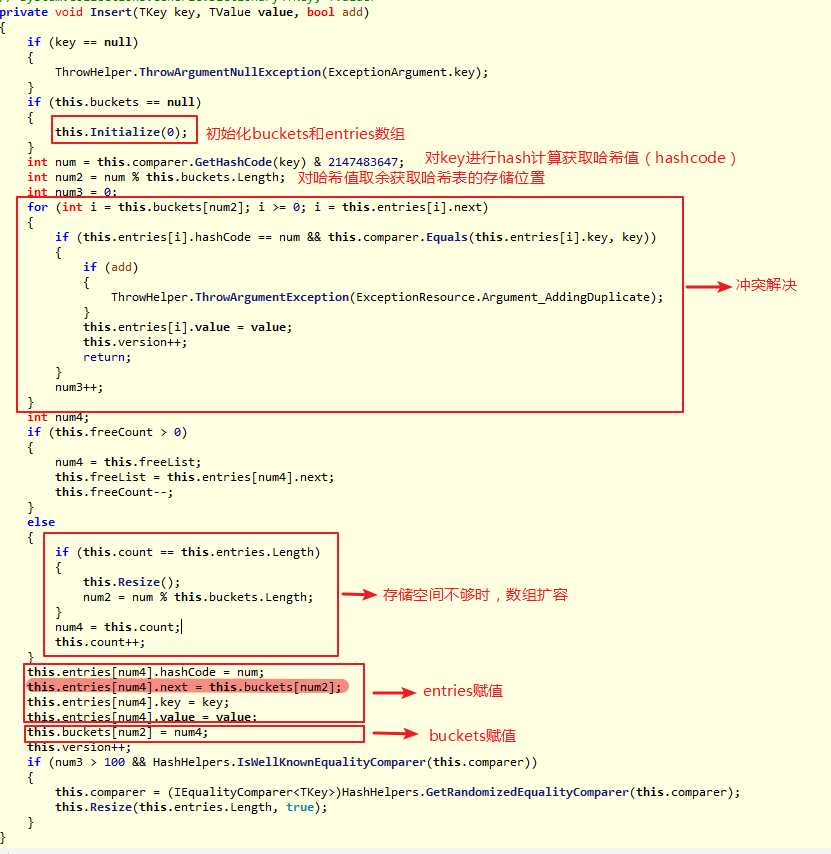
Dictionary<TKey,TValue>添加新元素的实现：

技术图片

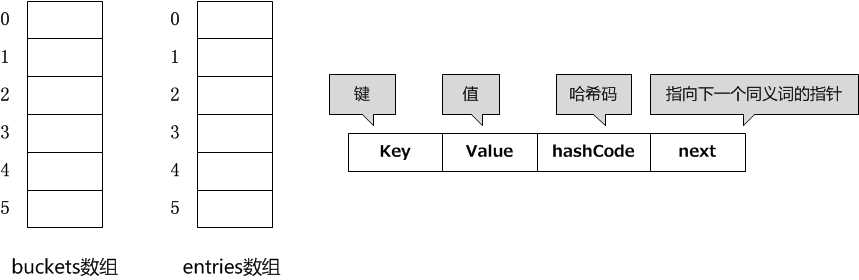
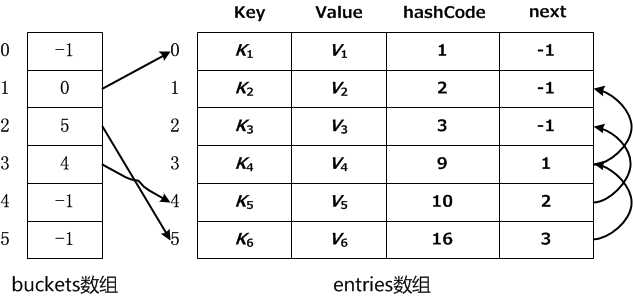
Dictionary<TKey,TValue>内部有两个数组，一个数组名为buckets，用于存放由多个同义词组成的静态链表头指针（链表的第一个元素在数组中的索引号，当它的值为-1时表示此哈希地址不存在元素）；另一个数组为entries，它用于存放哈希表中的实际数据，同时这些数据通过next指针构成多个单链表。entries数组中所存放的是Entry结构体，Entry结构体由4个部分组成，如下所示：

技术图片

Dictionary<TKey,TValue>计算key的哈希值使用的是取余法，这种方式可能会产生冲突，所以需要进行冲突解决。Dictionary<TKey,TValue>解决冲突的方式是链接法。

技术图片

我们可以根据源码来模拟推导一下这个过程：

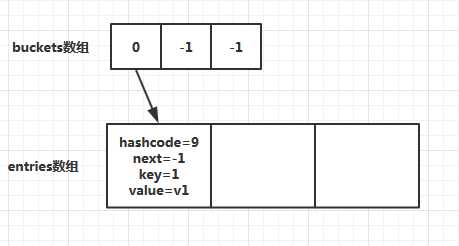
当添加第一个元素时，此时会分配哈希表buckets数组和entries数组的空间和初始大小，默认为3。对key=1进行哈希求值，假设第一个元素的哈希值=9，然后targetBucket = 9%buckets.Length(3)的值为0，所以第一个元素应该放在entries数组的第一位。最后对哈希表buckets数组赋值，数组索引为0，值为0。此时内部结构如图所示：

技术图片

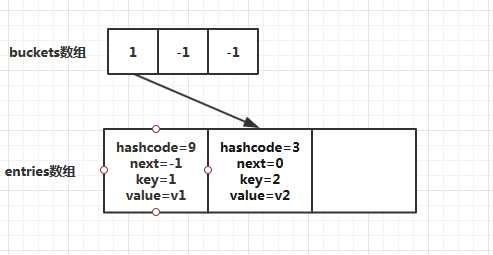
然后插入第二个元素，对key=2进行哈希求值，假设第二个元素的哈希值=3，然后targetBucket = 3%buckets.Length (默认是3)的值为0，所以第二个元素应该放在entries数组的第一位。但是entries数组的第一位已经存在元素了，这就发生了冲突。Dictionary<TKey,TValue>解决冲突的方式是链接法，把发生冲突的元素链接之前元素的后面，通过next属性来指定冲突关系，最后更新哈希表buckets数组。此时内部结构如图所示：

技术图片

我们可以通过Dictionary<TKey,TValue>查找元素的实现来证明我们上面的分析是正确的。

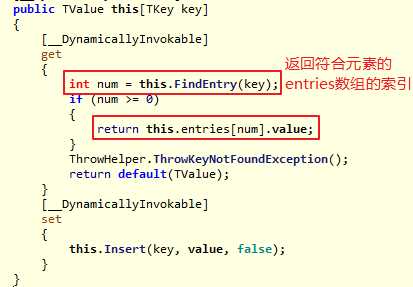
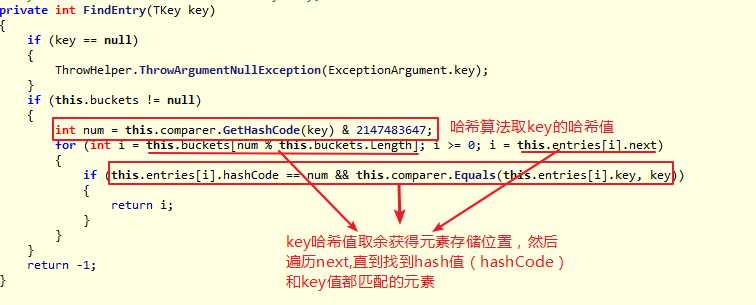
Dictionary<TKey,TValue>查找元素的实现：

技术图片

Dictionary<TKey,TValue>之所以能实现快速查找元素，其内部使用哈希表来存储元素对应的位置，我们可以通过哈希值快速地从哈希表中定位元素所在的位置索引，从而快速获取到key对应的Value值。物极必反，Dictionary<TKey,TValue>的缺点也很明显，就是里面的数据是无序排列的，所以按照一定顺序遍历查找数据效率是非常低的。

2.SortedDictionary<TKey,TValue>

SortedDictionary<TKey,TValue>和Dictionary<TKey,TValue>类似，至于区别我们从名称上就可以看出来，Dictionary<TKey,TValue>是无序的，SortedDictionary<TKey,TValue>则是有序的。key要保证唯一，而且还要有序排列，这让我们很自然的就想到了搜索二叉树。SortedDictionary<TKey,TValue>使用一种平衡搜索二叉树——红黑树，作为存储结构。因为基于二分查找，所以添加、查找、删除元素的时间复杂度是O(log n)。相对于下面提到的SortedList<TKey,TValue>来说，SortedDictionary<TKey,TValue>在添加和删除元素时更快一些。如果想要快速查询的同时又能很好的支持排序的话，并且添加和删除元素也比较频繁，可以使用SortedDictionary<TKey,TValue>。

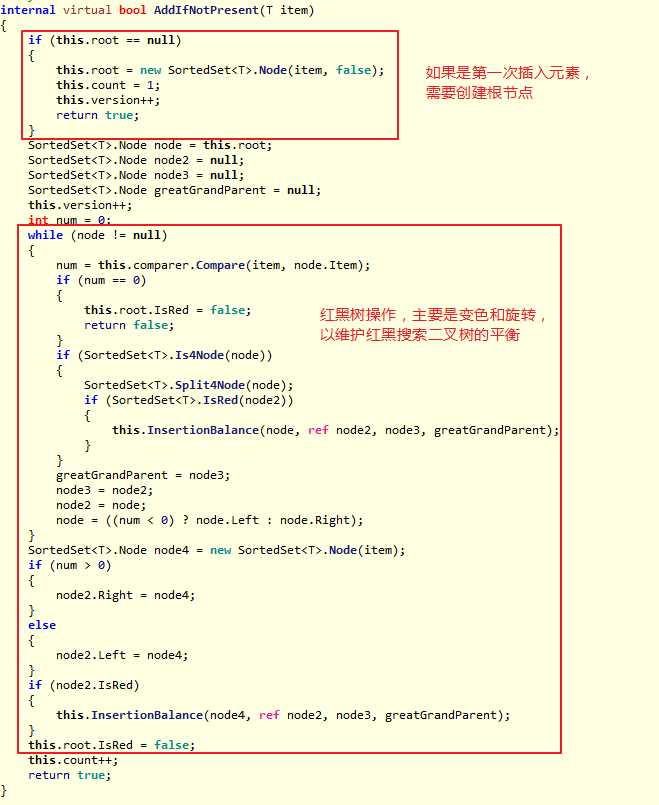
SortedDictionary<TKey,TValue>添加新元素的实现：

技术图片

3.SortedList<TKey,TValue>

在既需要快速查找又需要顺序排列的场景下，Dictionary<TKey,TValue>就无能为力了，因为Dictionary<TKey,TValue>使用了散列函数，并不支持线性排序。我们可以使用SortedList<TKey,TValue>集合类来应对这种场景。

SortedList<TKey,TValue>集合内部是使用数组实现的，添加和删除元素的时间复杂度是O(n)，查找元素利用了二分查找，所以查找元素的时间复杂度是O(log n)。所以SortedList<TKey,TValue>虽然支持了有序排列，但是却是以牺牲查找效率为代价的。

SortedList<TKey,TValue>和SortedDictionary<TKey,TValue>同时支持快速查询和排序，SortedList<TKey,TValue> 优势在于使用的内存比 SortedDictionary<TKey,TValue> 少；但是SortedDictionary<TKey,TValue>可对未排序的数据执行更快的插入和移除操作：它的时间复杂度为 O(log n)，而 SortedList<TKey,TValue> 为 O(n)。所以SortedList<TKey,TValue>适用于既需要快速查找又需要顺序排列但是添加和删除元素较少的场景。

内部实现结构：

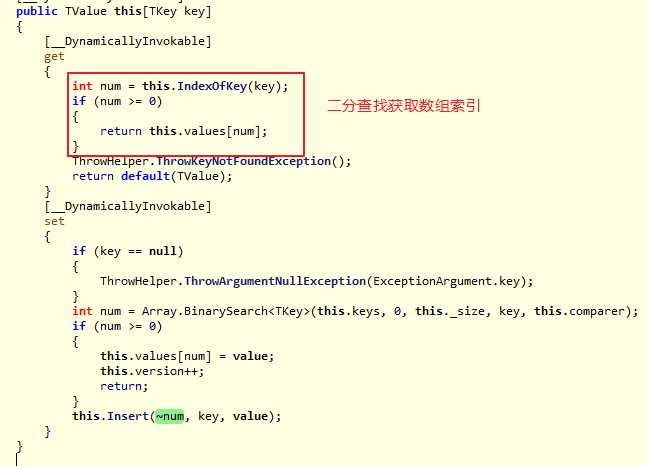
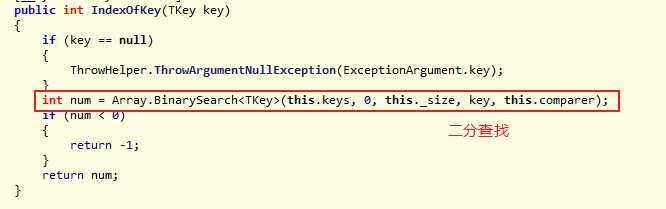
根据Key获取Value的实现：

IndexOfKey实现：

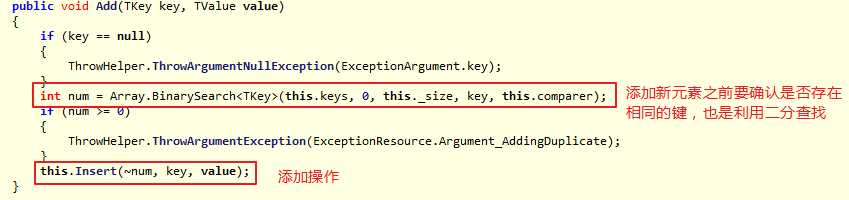
添加新元素：

添加操作：

非关联性泛型集合类

1.List

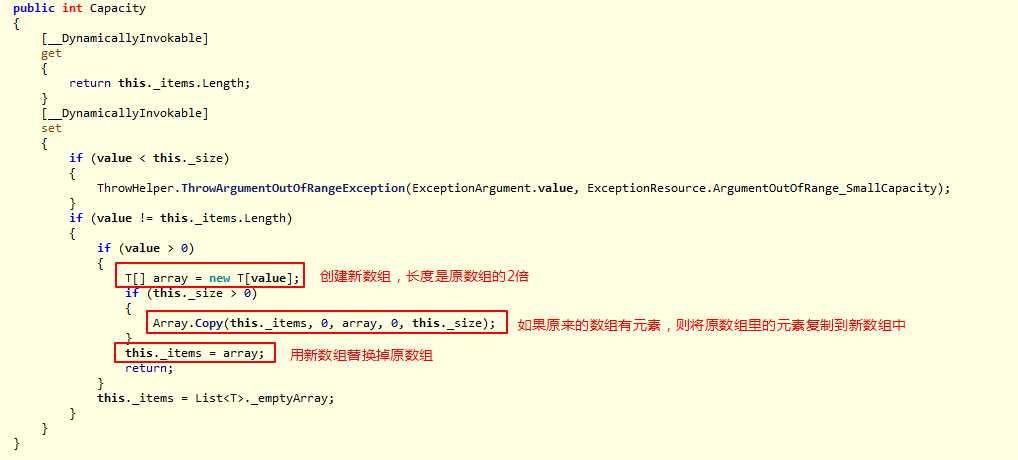
泛型的List 类提供了不限制长度的集合类型，List内部实现使用数据结构是数组。我们都知道数组是长度固定的，那么List不限制长度必定需要维护这个数组。实际上List维护了一定长度的数组（默认为4），当插入元素的个数超过4或初始长度时，会去重新创建一个新的数组,这个新数组的长度是初始长度的2倍，然后将原来的数组赋值到新的数组中。

我们可以通过ILSpy看一下List源码证明我们上面所说的：

List内部重要变量：

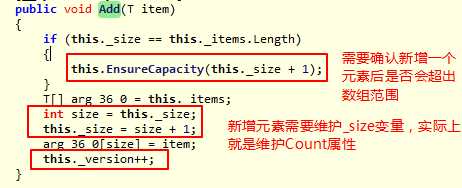
新增元素操作：

新增元素确认数组容量：

真正的数组扩容操作：

数组扩容的场景涉及到对象的创建和赋值，是比较消耗性能的。所以如果能指定一个合适的初始长度，能避免频繁的对象创建和赋值。再者，因为内部的数据结构是数组，插入和删除操作需要移动元素位置，所以不适合频繁的进行插入和删除操作；但是可以通过数组下标查找元素。所以List适合读多写少的场景。

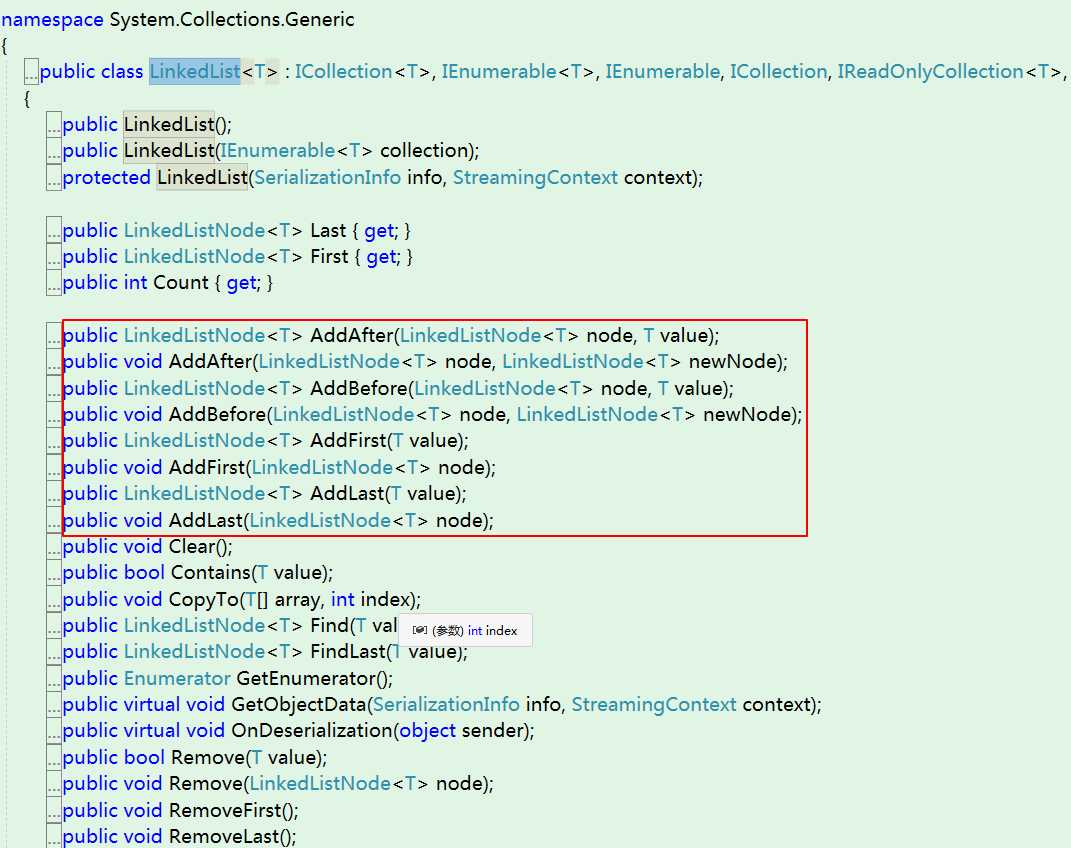
2.LinkedList

上面我们提到List适合读多写少的场景，那么必定有一个List适合写多读少的场景，就是这货了——LinkedList。至于为什么适合写多读少，熟悉数据结构的同学应该已经猜到了。因为LinkedList的内部实现使用的是链表结构，而且还是双向链表。直接看源码：

技术图片

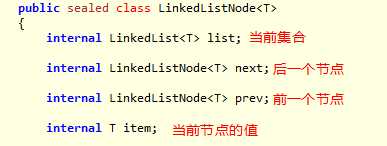
因为内部实现结构是链表，所以可以在某一个节点前或节点后插入新的元素。

链表节点定义：

技术图片

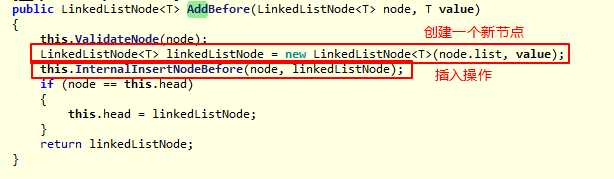
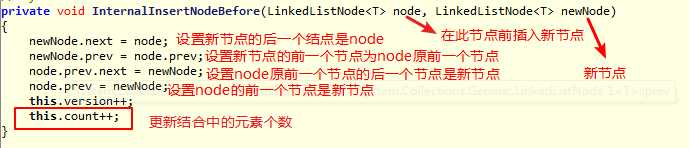
我们以在某个节点前插入新元素为例：

技术图片

具体的插入操作，注意操作步骤不能颠倒：

技术图片

3.HashSet

HashSet是一个无序的能够保持唯一性的集合。我们可以将HashSet看作是简化的Dictionary<TKey,TValue>，只不过Dictionary<TKey,TValue>存储的键值对对象，而HashSet存储的是普通对象。其内部实现也和Dictionary<TKey,TValue>基本一致，也是散列函数加双数组实现的,区别是存储的Slot结构体不再有key。

内部实现数据结构：

m_slots中所存放的是Slot结构体，Slot结构体由3个部分组成，如下所示：

技术图片

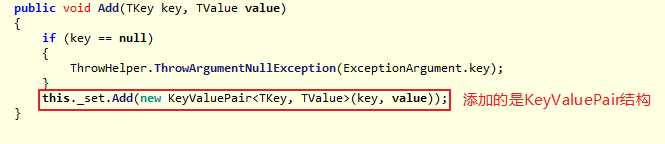
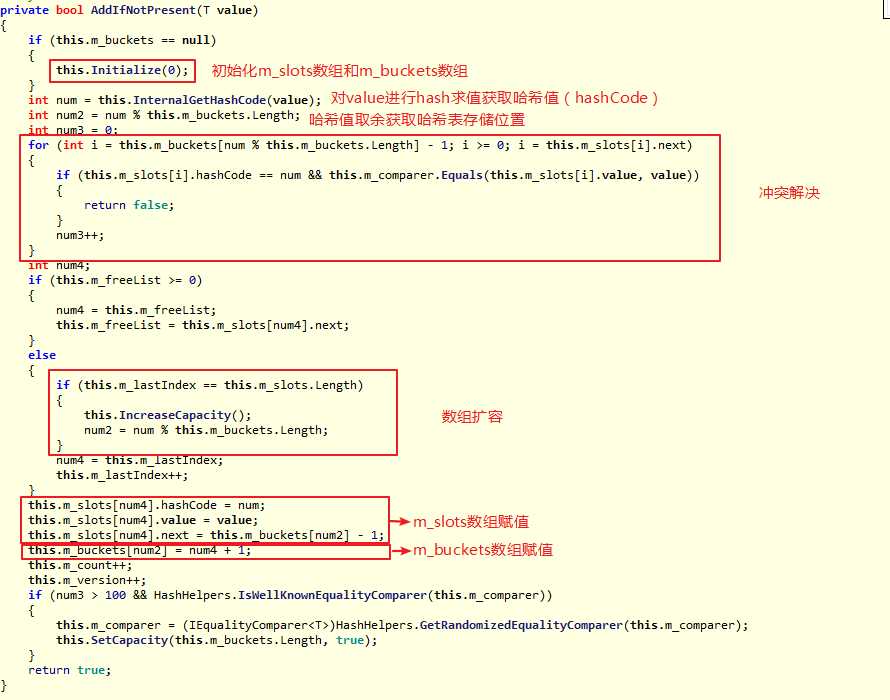
添加新元素的具体实现：

和Dictionary<TKey,TValue>添加新元素的实现基本一致。

技术图片

4.SortedSet

SortedSet和HashSet,就像SortedDictionary<TKey,TValue>和Dictionary<TKey,TValue>一样。SortedSet支持元素按顺序排列，内部实现也是红黑树，并且SortedSet对于红黑树的操作方法和SortedDictionary<TKey,TValue>完全相同。所以不再做过多的分析。

5.Stack

栈是一种后进先出的结构，C#的栈是借助数组实现的，考虑到栈后进先出的特性，使用数组来实现貌似是水到渠成的事。

技术图片

入栈操作：

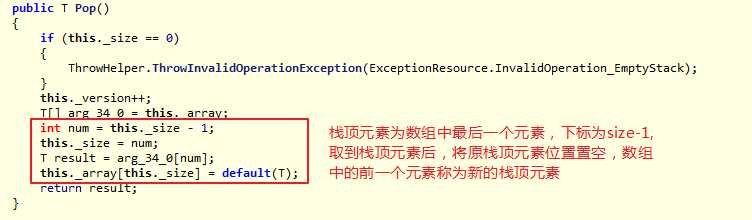
弹栈操作：

6.Queue

队列是一种先进先出的结构，C#的队列也是借助数组实现的，有了前面的经验，借助数组实现必然会有数组扩容。C#的队列实现其实是循环队列的方式，可以简单的理解为将队列的头尾相接。至于为什么要这么做？为了节省存储空间和减少元素的移动。因为元素出队列时后面的元素跟着前移是非常消耗性能的，但是不跟着向前移动的话，前面就会一直存在空闲的空间浪费内存。所以使用循环队列来解决这种问题。

技术图片