P3740 [HAOI2014]贴海报 离散化+线段树

Posted 2021-12-02 bxd123

　　

题目描述

Bytetown城市要进行市长竞选，所有的选民可以畅所欲言地对竞选市长的候选人发表言论。为了统一管理，城市委员会为选民准备了一个张贴海报的electoral墙。

张贴规则如下：

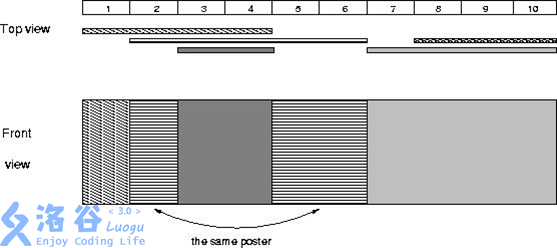
1. electoral墙是一个长度为N个单位的长方形，每个单位记为一个格子；

2. 所有张贴的海报的高度必须与electoral墙的高度一致的；

3. 每张海报以“A B”表示，即从第A个格子到第B个格子张贴海报；

4. 后贴的海报可以覆盖前面已贴的海报或部分海报。

现在请你判断，张贴完所有海报后，在electoral墙上还可以看见多少张海报。

输入输出格式

输入格式：

 

第一行： N M 分别表示electoral墙的长度和海报个数

接下来M行: Ai Bi 表示每张海报张贴的位置

 

输出格式：

 

输出贴完所有海报后，在electoral墙上还可以看见的海报数。

 

输入输出样例

输入样例#1： 复制

100 5
1 4
2 6
8 10
3 4
7 10

输出样例#1： 复制

4

说明

【约束条件】

1 0<= N <= 10000000 1<=M<=1000 1<= Ai <= Bi <=10000000

所有的数据都是整数。数据之间有一个空格

 

数据太大要进行离散化

然后区间染色

query有一点不一样  必须要读到叶结点 然后统计颜色即可

#include<bits/stdc++.h>
using namespace std;
//input by bxd
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i>=(b);--i)
#define RI(n) scanf("%d",&(n))
#define RII(n,m) scanf("%d%d",&n,&m)
#define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k)
#define RS(s) scanf("%s",s);
#define ll long long
#define pb push_back
#define CLR(A,v)  memset(A,v,sizeof A)
//////////////////////////////////
#define inf 0x3f3f3f3f
#define lson l,m,pos<<1
#define rson m+1,r,pos<<1|1
const int N=100000+5;
int sum[N<<2],col[N<<2],tot[N<<2];
int n,L[N],R[N],a[N],cnt,len,vis[N],ans;

int find1(int L,int R,int x)
{
    while(L<=R)
    {
        int m=(L+R)>>1;
        if(a[m]==x)return m;
        else if(a[m]>x)R=m-1;
        else L=m+1;
    }
}
void down(int pos)
{
    if(sum[pos])
    {
        sum[pos<<1]=sum[pos<<1|1]=col[pos];
        col[pos<<1]=col[pos<<1|1]=col[pos];
        sum[pos]=0;
    }
}
void update(int L,int R,int v,int l,int r,int pos)
{
    if(L<=l&&r<=R)
    {
        sum[pos]=col[pos]=v;
        return ;
    }
    down(pos);
    int m=(l+r)>>1;
    if(L<=m)update(L,R,v,lson);
    if(R>m)update(L,R,v,rson);
}
void  query(int L,int R,int l,int r,int pos)
{
    if(l==r)
    {
        tot[sum[pos]]++;
        return ;
    }
    down(pos);
    int m=(l+r)>>1;
    if(L<=m)query(L,R,lson);
    if(R>m)query(L,R,rson);
}

int main()
{
    RI(n);int m;RI(m);

    rep(i,1,m)
    {
        RII(L[i],R[i]);
        a[++cnt]=L[i];
        a[++cnt]=R[i];
    }

    sort(a+1,a+1+cnt);
    len=1;
    rep(i,2,cnt)
    if(a[i]!=a[i-1])a[++len]=a[i];
    repp(i,len,2)
    if(a[i]-a[i-1]>1)a[++len]=a[i]-1;
    sort(a+1,a+1+len);

    rep(i,1,m)
    {
        int l=find1(1,len,L[i]);
        int r=find1(1,len,R[i]);
        update(l,r,i,1,len,1);
    }

    query(1,len,1,len,1);

    ans=0;
    rep(i,1,m)if(tot[i])ans++;

    cout<<ans;

    return 0;
}

View Code