动态规划

Posted 2021-11-30 yusq77

算法思想

将待求解的问题分解为若干个子问题，按顺序求解子问题，同时前一子问题的解，为后一子问题的求解提供了有用的信息。

算法优点

针对每一个状态只需要进行一次运算，之后就可以重复利用这个状态的值，从而减少了大量不必要的重复计算。也就是，一旦出现重复的子问题求解，优先考虑动态规划方式求解，一般都会获得很多优化

算法特点

• 求解子问题时只保存针对当前子问题的最优解
• 重叠子问题，减少重复计算，对每一个子问题只解一次，将其不同阶段的不同状态保存在一个数组中。
• 子问题往往不是互相独立的

动态规划条件

• 总问题可划分为多个子问题
• 通过子问题的最优解可以获得整个问题的最终最优解
• 子问题必须具有无后效性。当前状态的子问题的解不会被之后状态的子问题影响
• 动态规划的子问题不独立，单个子问题的最优解可以使用之前已解决的子问题的解，这也是动态规划的优点

求解步骤

• 子问题的划分。 按照一定的顺序把整个问题划分为若干个规模相等的子问题
• 子问题状态的确定。根据问题需求和子问题的各个属性确定子问题的”状态“，同时需要满足无后效性。
• 推导状态转移方程。 状态转移指的就是根据上一个状态（或者叫上一个子问题的解）来获取当前子问题解的过程
• 边界条件和初始值的确定。由于动态规划是根据之前子问题的解来推导当前子问题的解，所以最初状态的值必须确定。边界条件是用来描述结束状态的，如果当前状态完全到达边界，便视为已经到达了最终状态。

算法实例

问题1：斐波那契数列

数列由1，1开始，之后的斐波那契数列系数就由之前的两数相加。

Sequence： 1，1，2，3，5，8，13，21，34，……

状态转移方程：

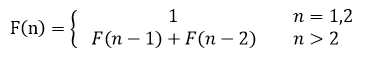
问题2：收益最大

纵轴是所作的任务，以及收益；横轴是对应任务所对应的时间。选取规则为时间不能重叠，使得收益最大。

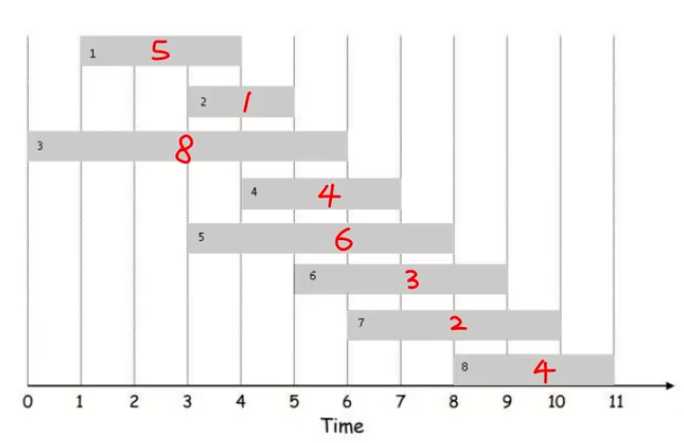
任务编号：       1，2，3，4，5，6，7，8

任务对应收益v(i)：5，1，8，4，6，3，2，4

第i个任务选状态（选和不选）最优解opt(i)：

pre(i)为之前的状态，对应任务编号的先前状态表：

i:       1  2  3  4  5  6  7   8             
pre(i):  0  0  0  1  0  2  3   5               
opt(i):  5  5  8  9  9  9  10  13 

问题3：不相邻元素总和最大

给定一个数组，选取一些元素使得总和最大，选取规则为不能连续取两个元素，即选取的元素之间至少要间隔一个其它元素，每个元素都有选与不选两种可能，使得用动态规划求解。

arr： 1，2，4，1，7，8，3

状态转移方程

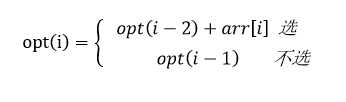
出口条件

opt[0] = arr[0]             
opt[1] = max(arr[0], arr[1])

详细代码

#!/usr/bin/python

import numpy as np

arr = [1, 2, 4, 1, 7, 8, 3]

# 递归方式
def rec_opt(arr, i):
    if(i == 0):
        return arr[0]
    elif(i == 1):
        return max(arr[0], arr[1])
    else:
        A = rec_opt(arr, i-2) + arr[i]
        B = rec_opt(arr, i-1)
        return max(A, B)

# 使用数组存储中间值
def dp_opt(arr):
   opt = np.zeros(len(arr))
   opt[0] = arr[0]
   opt[1] = max(arr[0], arr[1])
   for i in range(2, len(arr)):
       A = opt[i-2] + arr[i]
       B = opt[i-1]
       opt[i] = max(A, B)
    return opt[len(arr) - 1]

if __name__ == ‘__main__‘:
    print(rec_opt(arr, 6))   # 递归方式
    print ( dp_opt(arr))     # 使用数组存储中间值

问题4：寻找和为定值的数

给定一个数组，选取一些元素使得总和为给定的值。

arr：  3，34，4，12，5，2
s：    9

subset(arr, i, s)：数组arr当前第i个数字需要计算的和为s

状态转移方程

if s = =0:                              
    return true                             
elif i == 0:                                    
    return arr[0] == s                         
elif arr[i] > s:                           
    return subset(arr, i-1, s)   

使用二维数组进行存储结果

arr   i    0  1  2  3  4  5  6  7  8  9        s          
3     0    F  F  F  F  F  F  F  F  F  F                               
34    1    T                                               
4     2    T                                                    
12    3    T                                                       
5     4    T                                                      
2     5    T                                                  

详细代码

#!/usr/bin/python
import numpy as np

arr = [3,34,4,12,5,2]

# 递归方式
def rec_subset(arr,i,s):
    if s == 0:
        return True
    elif i == 0:
        return arr[0]==s
    elif arr[i] > s:
        return rec_subset(arr,i-1,s)
    else:
        A=rec_subset(arr,i-1,s-arr[i])
        B=rec_subset(arr,i-1,s)
        return A or B
def rec_subset_test():
    print(rec_subset(arr, len (arr)-1, 9))      #True
    print(rec_subset(arr, len (arr)-1, 10))     #True
    print(rec_subset(arr, len (arr)-1, 11))     #True
    print(rec_subset(arr, len (arr )-1, 12))    #True
    print(rec_subset(arr, len (arr)-1, 13 ))    #False

# 二维数组存储结果
def dp_subset(arr, S):
    subset = np.zeros((len(arr), S+1), dtype = bool)
    subset[:, 0] = True
    subset[0, :] = False
    subset[0, arr[0]] = True
    for i in range(1, len(arr)):
        for s in range(1, S+1):
            if(arr[i] > s):
                subset[i, s] = subset[i-1, s]
            else:
                A = subset[i-1, s-arr[i]]
                B = subset[i-1, s]
                subset[i, s] = A or B
    r,c = subset.shape
    return subset[r-1, c-1]

def dp_subset_test():
    print(dp_subset(arr, 9))      #True
    print(dp_subset(arr, 10))     #True
    print(dp_subset(arr, 11))     #True
    print(dp_subset(arr, 12))     #True
    print(dp_subset(arr, 13))     #False

# 当.py文件被直接运行时，if下的代码块将被运行；
# 当.py文件以模块形式被导入时，if下的代码块不被运行。
if __name__ == ‘__main__‘:
    rec_subset_test()
    dp_subset_test()