0.618法(近似黄金分割法)实验
Posted wangxingwu12138
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了0.618法(近似黄金分割法)实验相关的知识,希望对你有一定的参考价值。
实验环境
语言:Python3.7
软件:Pycharm
算法步骤:

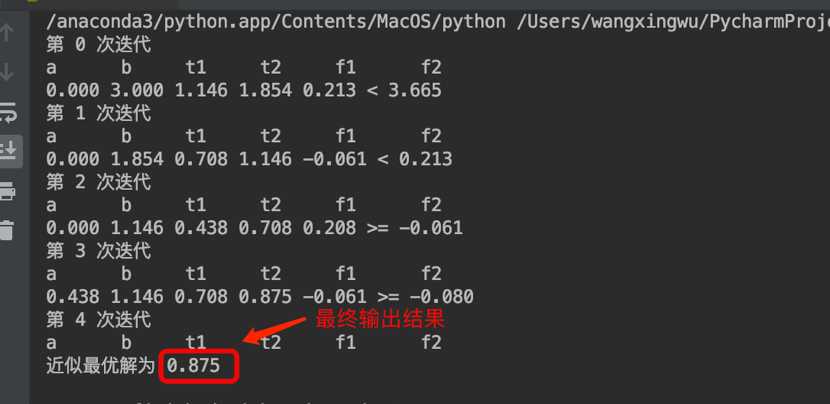
实验结果
通过程序运行,我们发现程序进行了4次迭代,在第4次迭代时结束运行,观察输出结果,最优解约为0.875,与教材上答案一致。
Python代码
def face(x):
return x**3-2*x+1 #目标函数
def mark(a,b):
if a>=b:
return ">="
else:
return "<"
def HJFG(a,b,eps):
lamb=0.618
t1=a+(1-lamb)*(b-a)
t2=a+lamb*(b-a)
f1=face(t1)
f2=face(t2)
i=0
print("第",i,"次迭代")
print("a b t1 t2 f1 f2")
print(‘%.3f‘ %a, ‘%.3f‘ %b, ‘%.3f‘ %t1, ‘%.3f‘ %t2, ‘%.3f‘ %f1,mark(f1,f2), ‘%.3f‘ %f2)
while(b-a>eps):
i=i+1
print("第", i, "次迭代")
print("a b t1 t2 f1 f2")
if f1<=f2: #第三步
if t2-a<=eps: #第四步
print("近似最优解为", ‘%.3f‘ % t1)
break
else:
b=t2
t2=t1
t1=b-lamb*(b-a)
f2=f1
f1=face(t1)
print(‘%.3f‘ % a, ‘%.3f‘ % b, ‘%.3f‘ % t1, ‘%.3f‘ % t2, ‘%.3f‘ % f1, mark(f1, f2), ‘%.3f‘ % f2)
else:
if b-t1<=eps:
print("近似最优解为",‘%.3f‘ % t2)
break
else:
a=t1
t1=t2
t2=a+lamb*(b-a)
f1=f2
f2=face(t2)
print(‘%.3f‘ % a, ‘%.3f‘ % b, ‘%.3f‘ % t1, ‘%.3f‘ % t2, ‘%.3f‘ % f1, mark(f1, f2), ‘%.3f‘ % f2)
HJFG(0,3,0.5)
以上是关于0.618法(近似黄金分割法)实验的主要内容,如果未能解决你的问题,请参考以下文章