各种距离

Posted 2021-11-29 blueheart0621

 1. 欧几里得距离

 

 给定空间中两个点（x₁,y₁）,（x₂,y₂）；它们之间的欧几里得距离公式为：((x₁-x₂)²+(y₁-y₂)²)^1/2，即两个点之间的直线距离。本质是向量的2-范数。

 

2. 曼哈顿距离

给定空间中两个点（x₁,y₁）,（x₂,y₂）；它们之间的曼哈顿距离公式为：|x₁-x₂|+|y₁-y₂|，即两个点之间的水平距离绝对值加上垂直距离的绝对值。本质是向量的1-范数。

3. 切比雪夫距离

 给定空间中两个点（x₁,y₁）,（x₂,y₂）；它们之间的切比雪夫距离公式为：max(|x₁-x₂|, |y₁-y₂|)，即两点之间横纵坐标距离绝对值的最大值。本质是向量的∞-范数。

 

[联系]

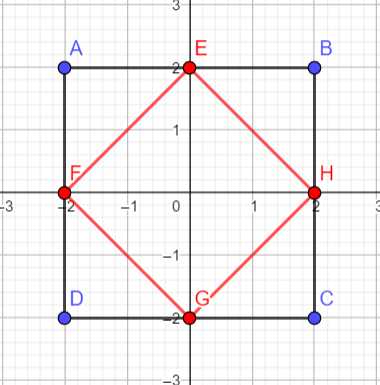
 如下图所示，矩形EFGH是到原点曼哈顿距离为2的点的集合，矩形ABCD是到原点切比雪夫距离为2的点的集合。

 

4. 闵可夫斯基距离

 

 给定空间中两个点（x₁,y₁）,（x₂,y₂）；它们之间的闵可夫斯基距离公式为：((x₁-x₂)^p+(y₁-y₂)^p)^1/p。本质是向量的范数，p取不同的值时对应不同的p-范数。