最短路算法分析

Posted 2021-11-27 wuxiangnong

最短路算法分析

如下图所示，我们把边带有权值的图称为带权图。边的权值可以理解为两点之间的距离。一张图中任意两点间会有不同的路径相连。最短路就是指连接两点的这些路径中最短的一条。

---

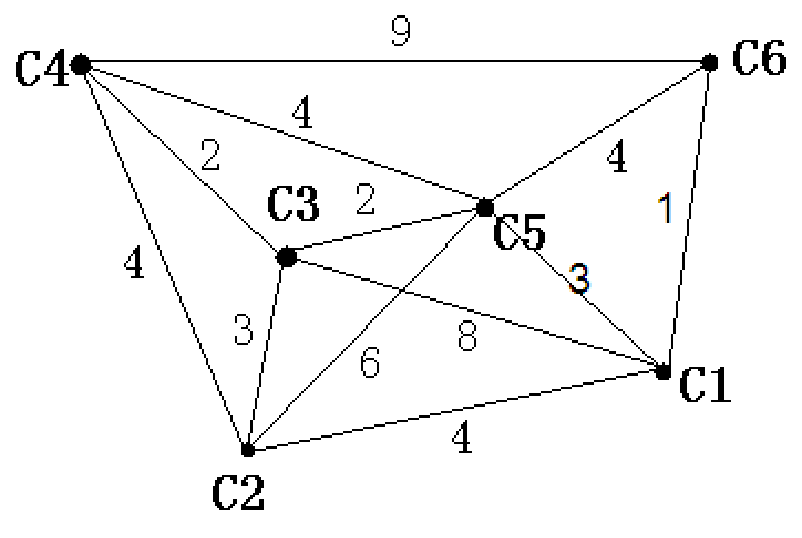
对于所有求最短路的算法，都是基于一个最基础的思想，那就是：松弛。
什么叫松弛呢？简单的说，就是刷新最短路。
那，怎么刷新呢？我们想，能刷新最短路的有啥？就是用最短路（边也可能是最短路）。要用魔法打败魔法

---

以下图为例，点1到点3的距离是2，点3到点2的距离是1，而图中1到2的距离是6，那么，很明显点1到点3到点2比点1直接到点2短得多，那么，我们的最短路dis[1][2]就等于dis[1][3]+dis[3][2]。我们可以这么理解：1到3这条边的边权已经是1到3的最短路了，同样，2到3也是，那我们就可以用这两条最短路来刷新1到2的最短路，这就是用最短路来松弛最短路了。

---

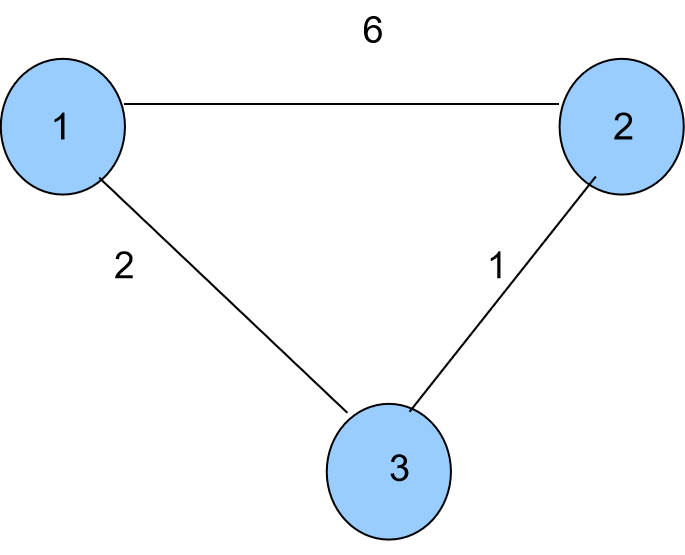
那么，基于松弛操作，我们就有了非常多种求最短路的算法，这些算法各有神通，各有缺陷，都应该熟练掌握且能在考场上准确判断该用那种算法。

1、Floyed:

学过最短路的人，大多数都会认为：Floyed就是暴力，简单粗暴，简单得很。其实，如果你仔细品读这个算法，会发现：虽然代码简单，但是其思想却非常的巧妙！
我们来分析一下：

我们要求最短路，我们需要通过中转点来进行松弛，那我们要怎么找中转点呢？

显然，必须得枚举。那，怎么枚举呢？我们自己画画图就知道，一些最短路可以拐来拐去，也就是中转点有很多，那我们怎么枚举？这就是Floyed的巧妙之处，它用到的是动态规划的思想。

对于规模很大的问题，我们的一般策略应该是：缩小规模。不管它可能有多少个，我们慢慢从少往多推。

假设我们现在不允许有中转点，那么各个点之间的最短路应该是题目给出来的边权。

现在我们只允许通过1号节点来进行转移，注意是1号而不是1个，如果讨论个数的话其实就回到了我们上面的问题：“怎么枚举？”。现在我们只需要枚举i和j，比较dis[i][1]+dis[1][j]和dis[i][j]的大小，如果小于则刷新，这就是松弛。注意这里i不一定小于j，我们现在的对象是图，图描述的是元素间的网状关系，不同于顺序表描述的顺序关系。

接着，我们允许通过1号点和2号点进行转移，注意这里的“和”，一方面，2号点本身可以独自松弛一些路径，另一方面，之前通过1号点松弛的一些路径中，可能有和2号点连着的，什么意思呢？比如说，在上一轮我们用dis[5][1]+dis[1][2]松弛了dis[5][2]，然后我们再用这个路径去松弛其他路径，实际上就相当于通过1号点和2号点进行转移，所以我们的条件是“允许通过1号点和2号点”，这也就解决了我们的问题：“怎么找中转点？”。不必考虑中转点的数量，用编号更大的点做中转点时，实际上也包含了编号小的中转点。

所以，这里我们仍然只需要枚举i和j，用dis[i][2]+dis[2][j]去尝试松弛dis[i][j]就行了，这里的中转点我们可以用k来表示。

所以，我们需要三重循环：第一重枚举中转点，k=1~n，第二重就是起点i，也是从1~n，第三重终点j也是一样的，这里的k循环一定要在最外层，如果不在最外层，就有可能将k号点可以松弛的边漏掉，影响结果。在循环最里面判断dis[i][k]+dis[k][j]是否比dis[i][j]来的优，是的话则更新，这就是Floyed算法的实现。

核心代码：

for(k=1;k<=n;k++)
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            if(dis[i][j]>dis[i][k]+dis[k][j])
                dis[i][j]=dis[i][k]+dis[k][j];

根据这种算法，我们还需注意初始化的问题：题目没有给出连边的两个点应该初始化为无穷大，这样才能满足我们的判断条件，另外一个点到它本身的距离应该初始化为0，也是为了满足判断条件，因为中转点可能在起点或终点上。

Floyed算法的功能非常强大，根据代码我们可以发现：它可以求出任意两点之间的最短路，而且码量极小，可以处理所有情况的边权，但有一点：它无法处理负环，这个我们将结合Bellman-Ford一起说。它的劣势也十分明显：时间复杂度太高，只能处理n极小的图。那我们能不能进行优化呢？

答案是不行。所谓的优化，其实就是减少没必要的操作，但是对于这个算法，你可以在中间某一层循环结束后结束算法吗？不可以。我们的Floyed的松弛操作是通过枚举进行的，也就是无法保证最优，那能不能判断一下，当前这个k循环里有没有进行过松弛，如果没进行过就退出呢？

仔细想一想，这是一张图，你当前这个点没有用，不代表它后面的点也没有用，这只是编号的大小顺序而已，所以，无法优化。那，n如果稍微大一点，不就炸掉了？所以，我们来讲另外一种算法。

---

2、Dijkstra：

我们上面提到，Floyed慢的原因是它无法保证求得的最短路一定是最优的，那我们能不能保证每次求得最短路是最优的呢？肯定可以，但是，这时候我们的求的只能是一个点到其它点的最短路，因为你无法保证每一个点都能在某一轮找到与别的点的最短路，这就是Floyed的问题。求一个点到其它点的最短路的问题，称为单源最短路问题。Floyed处理的就是多源最短路问题。顺便说一下，Floyed是处理多源最短路的最优算法，也是我们的不二选择。所以，以下的算法都是求单源最短路的算法。

有了这样分析的基础，我们不难想到：用dis[i]记录i到源点（我们不妨称为x）的最短路，那么一开始，我们得到了许多由x连出的边，那我们想要得到一个不会再改变的最短路，也就是一个确定的dis[i]，我们怎么做？这里就要用到贪心的策略。不再改变，意味着无法进行松弛，那什么样的情况下dis[i]无法再进行松弛了呢？那就是不存在一个k使得dis[k]+l[k][i]（l表示边长）<dis[i]，也就是说，没有点可以转移这条路径，那说明这个i到x的距离一定是最短的，也就是dis[i]是所有dis[]中最小的，这样一定能保证这条路径是最短的，所以，我们需要找到一个dis[i]最小的点i，那么它到x的最短路已经确定了，我们拿它来进行松弛。这样，每一轮都可以确定一个点到源点x的最短路，只要经过n-1轮，我们就得到了任意一点到源点的最短路。

另外还要注意，我们已经求得最短路的点，我们还有必要再去管它吗？显然没有。也就是说，在找点的时候，我们要找的应该是还没有求得最短路的点，不然如果你这个点的最短路是全图最短路里最短的，那不是一直选你，然后做无用的重复判断？所以，我们还需要一个数组f[]来记录点i是否已求得最短路，f[i]=1表示已求得，f[i]=0表示未求得。

那么，实现的话，我们需要一层i来枚举还剩下的点数，i=1~n-1，里面要有一个j=1~n来找离源点最近的点t，然后标记f[t]，再用t来尝试进行松弛操作，还需要一次j循环。

核心代码：

for(i=1;i<=n-1;i++)
{
    int t,minn=100000001;
    for(j=1;j<=n;j++)
        if(f[i]==0&&dis[j]<minn)
        {
            minn=dis[j];
            t=j;
        }   
    f[t]=1;
    for(j=first[t];j;j=a[j].next)
        if(dis[a[j].to]>dis[t]+a[j].len)
            dis[a[j].to]=dis[t]+a[j].len;   
}

这里采用邻接表来存储，其优点不必阐述。另外，这里f[]要先初始化为0，然后dis[]初始化为无穷大，很好理解，另外要在题目给出的边中先初始化一些源点有连边的dis[i]=l[x][i]。f[x]=1，因为源点到本身的距离已经确定，也就带来了dis[x]=0。

实际上，Dijkstra只有比Floyed快这一优势，而且还不是因为它算法比较优秀，只是因为它减少了起点的枚举。而且，它只能求单源最短路，而且还不能处理负边权和负环。什么是负边权呢？负边权，顾名思义就是边权为负，那为什么Dijkstra不能处理呢？Dijkstra的策略是每次保证求得一条最短路，那你现在有了负边权，就无法保证我找到的距离源点最近的点一定是最近的了，那这个算法就废了。Floyed就可以解决这样的问题，因为它不管你的边权是什么样的，只管算就好了，不像Dijkstra有那样的要求，它只要保证最优子结构，你边权的正负并不会影响它的最优。

当然，这个算法还是可以优化的。我们要找一个距离源点最近的，那我们一定要一个一个去找吗？我们看到，这个最近的值是在一个区间里被挑出来的，那我们不难想到用堆来维护这个区间。这个堆的关键字是点到源点的距离，但是我们还要记点的编号，因为一会儿还要用点来进行松弛。取堆顶的点，用这个点尝试一波松弛，在这过程中，我们如果发现了被松弛的路径，那么这个终点就要入堆，因为被松弛意味着它到源点的距离变了，我们当然要把它入堆去和其它的点作比较。那么这种情况下，我们的初始化就只要将源点和0入堆就行了，不需要额外做dis[i]=w[x][i]，因为现在dis[i]是可以通过dis[x]+w[x][i]算出来的。

核心代码：

while(top!=0)
{
    int i,t=get();//get()表示删除堆顶并返回堆顶点的编号
    for(i=first[t];i;i=a[i].next)
        if(dis[a[i].to]>dis[t]+a[i].len)
        {
            dis[a[i].to]=dis[t]+a[i].len;
            put((node{dis[a[i].to],a[i].to});
//put表示将这条路径的重点a[i].to和a[i].to到源点的距离存入堆
        }
}

这里会出现一个点在堆中出现多次的问题，不必担心，这并不会影响我们的结果。因为堆中虽然有相同点，但堆中存储的它们到源点的距离一定各不相同，那么在进行松弛时，选的一定是最优的那一条路径，也就是dis最小的那一个，那么剩下就是多余的，会随着不断的取堆顶的操作一个个被清除，不必再单独考虑。

---

3、Bellman-Ford：

我们上面一直着重于找一个中转点来进行松弛，我们能不能不管中转点呢？当然可以。我们之前的策略是，找一个中转点，然后用它连的边实现松弛。我们现在不用中转点，那就简单点，直接找边，那我怎么知道要选哪条边？实际上你也无法知道。因为这不满足最优子结构。那，我们不妨把所有边的试一遍，实际上这不能称之为“边”，而应该称其为“路径”，你不可能拿几条边在那里一直玩，这里需要呈现出一个结构，一条条的边组成了路径。我们每次拿我们已知的可能的最短路径dis[k]来进行松弛：如果dis[k]+w[k][j]<dis[j]，刷新dis[j]，k是源点到每一个的最短路径“估计值”。那，这样一轮下来，我们可以得到一些新的最短路径，我们再利用这些最短路径来松弛，又可以得到新的最短路径，通过这样的方式一层一层建立起整个最短路的结构。那，这样的操作要进行多少轮呢？这就要看一个最短路中最多会包含几条边了。最多几条呢？不难想到，n个点的图，最短路径上最多有n-1条边。我们知道，连接n个点只需要n-1条边，再多了就会形成环，那环有没有可能是最短路呢？

不可能。假如我们这张图不存在负环，那重复走路肯定不优。如果存在负环呢？那我们就可以一直绕圈圈，就不存在最短路了。那，是不是这张图都没有最短路了呢？不是！只有可以到达负环的点才不存在最短路。

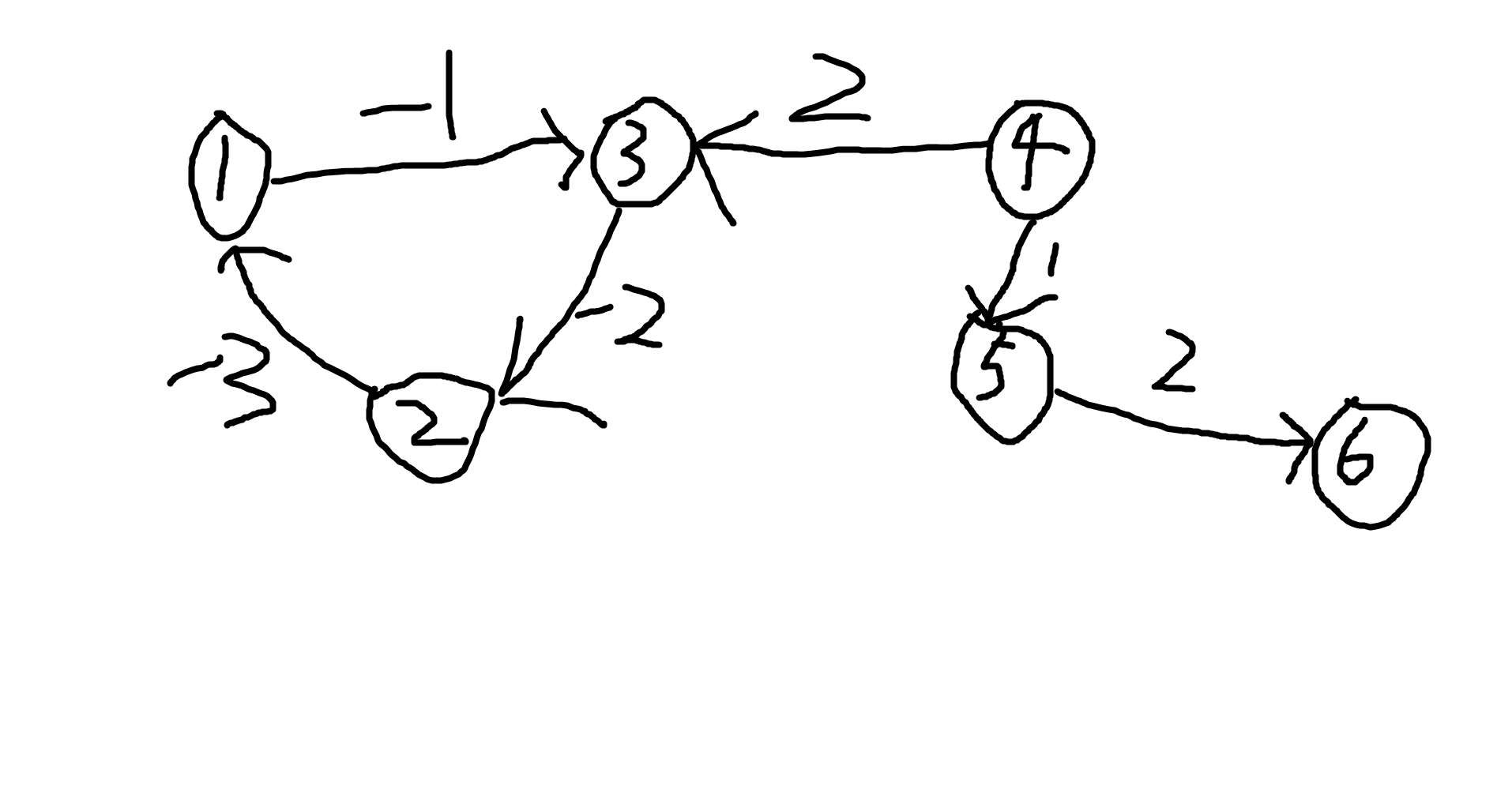
如图所示，对于在负环上及可以到达负环的点①②③④，都不存在最短路径，但是⑤却有一个最短路径：⑤->⑥的最短路径为2。为什么说④也没有最短路径呢？因为它可以到达负环，那它走的所有路径都可以先去负环里面多转几圈，只要进了负环里，就没有最短路了。因此，只要存在最短路径，那么最多经过n-1轮，一定可以求出所有的最短路径。
核心代码：

for(i=1;i<=n-1;i++)
    for(k=1;k<=n;k++)
        if(dis[u[i]]+w[i]<dis[v[i]])
            dis[v[i]]=dis[u[i]]+w[i];

这里因为主要涉及对单个边的操作，我们采用少见的边集数组，记录单个边的信息。i表示当前边的编号，u[i]表示这条边的起点，v[i]表示这条边的终点，w[i]表示这条边的权值（边权）。那么，刚才讲了什么事负环，还没讲怎么处理负环。Bellman-Ford处理负环非常简单，只要在n-1轮结束后判断一下：是否还能再进行松弛操作，也就是判断是否还有dis[v[i]]>dis[u[i]]+w[i]，如果有，那就说明这个源点会到到达一个负环，那对于这个源点就不存在最短路了。实际上，到了提高组，我们需要对负环做出处理，这就需要用到我们的Bellman-Ford来实现了，这里不必阐述。

那，Floyed为什么没法处理负环呢？实际上，Floyed也可以处理一些负环，关键是这个点必须在负环上。用Floyed我们可以直接表示环，就是dis[i][i]，如果dis[i][i]<0，我们知道，Floyed的dis[i][i]初始化都是为0，那就说明，出现了负环，且这个点就在负环上。但是，如果这个点不在负环上，但它可到达负环，那某些情况下Floyed就无法识别了，因为如果这个点不在负环上的话，它可以到负环，但是反过来，负环不一定可以到这个点，如果我的边是单向的，那不可能找到一个中转点来实现这个点到负环的最短路的松弛，因为从负环到这个点的长度是无限大，那这个dis[i][i]就是恒为0。当然，如果这张图是无向图，那Floyed也是可以处理负环的。

小优化：其实不难发现，有时候我们并不需要经过n-1轮才能求得结果，所以，我们可以在一轮结束以后判断：当前这一轮进行松弛，如果有，那才有继续下一轮的必要，如果没有，那就可以提前退出了，因为你已经没有任何一条路径可以再进行松弛了，你再下一轮只是再进行一论完全相同的操作，实在是没有必要。

---

4、SPFA：

根据我们上面的小优化，我们其实可以再进行一个大的优化。小优化说的是，出现被松弛过的路径，才有松弛成功的可能。如果一条路径已经无法松弛，那对于这个算法而言，这条路径就没用了。那么，我们怎么判断哪些最短路径被松弛过了呢？这样就不能看边了，而应该看点。如果dis[i]刷新了，那么说明这个i可以为我们接下来的松弛提供帮助，我们应该将它记录起来。一个点是可以松弛很多路径的，也就是会拓展出很多点，然后我们取出记录的第一个点，用这个点继续重复上面的操作：判断dis[i]是否大于dis[t]+w[t][i]，这里的t代表松弛的中转点，然后继续拓展节点，记录，最后把当前进行松弛的点删掉。取第一个，拓展，删除第一个，再取第一个，拓展，再删除，我们可以用队列来实现这一过程，因此SPFA也被称为是Bellman-Ford的队列优化。

还要注意一点，这个队列里的元素是可以重复入队的，因为一个点的最短路径可以不断更新。另外，当一个点已经在队列里的时候，我们是不用将它入队的，因为我们记录这个点的目的是等会要使用它，所以我们记的是它的编号，这里一定要和Dijkstra堆优化分清楚，Dijkstra需要的是它的路径长度，我们这里不需要，所以就算这个点的最短路径中间可能会变，但是不影响我们的结果，我们只需要记住这个点可能可以作为松弛的中转点，也就是我们可以用它进行松弛，就够了。

核心代码：

int head=0,tail=1;
q[head]=x;
f[x]=1;
dis[x]=0;
while(head<tail)
{
    int i,t=q[head];
    for(i=first[t];i;i=a[i].next)
        if(dis[a[i].to]>dis[t]+a[i].len)
        {
            dis[a[i].to]=dis[t]+a[i].len;
            if(f[a[i].to]==0)q[++tail]=a[i].to;
        }
   f[q[head]]=0;
    head++;
}

初始化的时候，我们需要将x入q数组，还要给x打上标记。对于dis[]，依旧不需要初始化dis[i]，但我们需要初始化dis[x]=0，不然我们无法用x进行松弛。至于为什么出队要放后面，这个是根据代码来定的，我们一开始的x存在q[head]里，所以要先处理完再出队，如果一开始x存在q[tail]里，那这个出队操作就要放在最前面了。

既然SPFA是Bellman-Ford的优化，那么Bellman-Ford能实现的功能SPFA也都能实现。负的边权正常算，如何判断负环呢？和Bellman-Ford的思想类似。一条最短路径上的边不会超过n-1条，反之，一条最短路径上的点也不会超过n个，所以如果一个点入队超过n次，那么这个点一定是和负环连着的，要么可达负环，要么就在负环上。

---

各算法的对比：

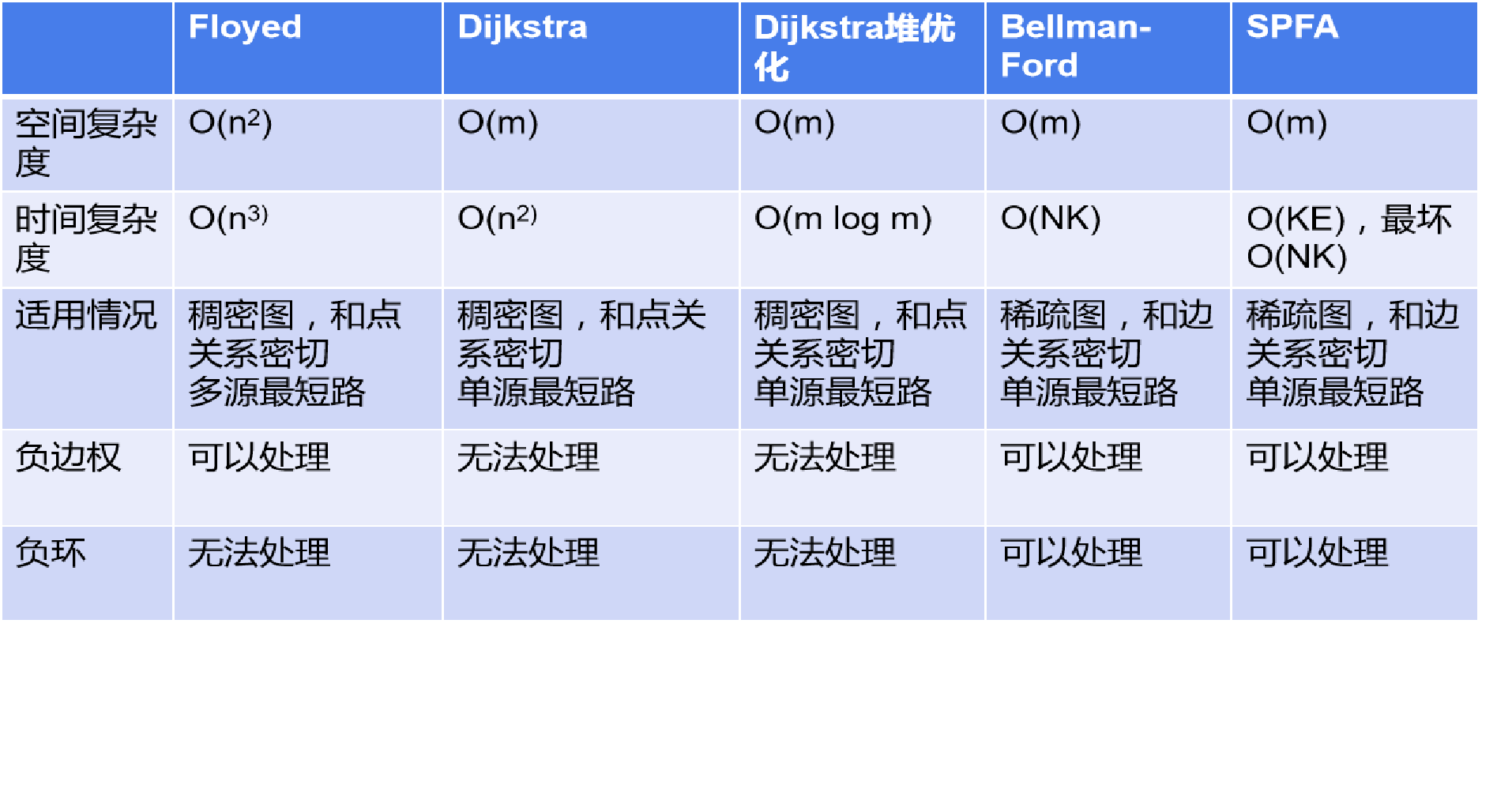
By wxn