第五章小结

Posted 2021-11-27 zasmn

第五章——树（生命不息，种树不止）

无序树：树中任意节点的子结点之间没有顺序关系，这种树称为无序树,也称为自由树;

有序树：树中任意节点的子结点之间有顺序关系，这种树称为有序树；

二叉树：每个节点最多含有两个子树的树称为二叉树；

完全二叉树

满二叉树

霍夫曼树：带权路径最短的二叉树称为哈夫曼树或最优二叉树；

在二叉树遍历方面有分为先序遍历，中序遍历，和后序遍历。

以下是一些二叉树操作的相关实现源码：

　　插入操作：

 1 struct node
 2 {
 3     int val;
 4     pnode lchild;
 5     pnode rchild;
 6 };
 7 
 8 pnode BT = NULL;
 9 
10 
11 //递归方法插入节点 
12 pnode insert(pnode root, int x)
13 {
14     pnode p = (pnode)malloc(LEN);
15     p->val = x;
16     p->lchild = NULL;
17     p->rchild = NULL;
18     if(root == NULL){
19         root = p;    
20     }    
21     else if(x < root->val){
22         root->lchild = insert(root->lchild, x);    
23     }
24     else{
25         root->rchild = insert(root->rchild, x);    
26     }
27     return root;
28 }
29 
30 //非递归方法插入节点 
31 void insert_BST(pnode q, int x)
32 {
33     pnode p = (pnode)malloc(LEN);
34     p->val = x;
35     p->lchild = NULL;
36     p->rchild = NULL;
37     if(q == NULL){
38         BT = p;
39         return ;    
40     }        
41     while(q->lchild != p && q->rchild != p){
42         if(x < q->val){
43             if(q->lchild){
44                 q = q->lchild;    
45             }    
46             else{
47                 q->lchild = p;
48             }        
49         }    
50         else{
51             if(q->rchild){
52                 q = q->rchild;    
53             }    
54             else{
55                 q->rchild = p;    
56             }
57         }
58     }
59     return;
60 }

View Code

    删除操作：

 1 bool delete_BST(pnode p, int x) //返回一个标志，表示是否找到被删元素 
 2 {
 3     bool find = false;
 4     pnode q;
 5     p = BT;
 6     while(p && !find){  //寻找被删元素 
 7         if(x == p->val){  //找到被删元素 
 8             find = true;    
 9         }    
10         else if(x < p->val){ //沿左子树找 
11             q = p;
12             p = p->lchild;    
13         }
14         else{   //沿右子树找 
15             q = p;
16             p = p->rchild;    
17         }
18     }
19     if(p == NULL){   //没找到 
20         cout << "没有找到" << x << endl;    
21     }
22     
23     if(p->lchild == NULL && p->rchild == NULL){  //p为叶子节点 
24         if(p == BT){  //p为根节点 
25             BT = NULL;    
26         }
27         else if(q->lchild == p){   
28             q->lchild = NULL;
29         }        
30         else{
31             q->rchild = NULL;    
32         }
33         free(p);  //释放节点p 
34     }
35     else if(p->lchild == NULL || p->rchild == NULL){ //p为单支子树 
36         if(p == BT){  //p为根节点 
37             if(p->lchild == NULL){
38                 BT = p->rchild;    
39             }    
40             else{
41                 BT = p->lchild;    
42             }
43         }    
44         else{
45             if(q->lchild == p && p->lchild){ //p是q的左子树且p有左子树 
46                 q->lchild = p->lchild;    //将p的左子树链接到q的左指针上 
47             }    
48             else if(q->lchild == p && p->rchild){
49                 q->lchild = p->rchild;    
50             }
51             else if(q->rchild == p && p->lchild){
52                 q->rchild = p->lchild;    
53             }
54             else{
55                 q->rchild = p->rchild;
56             }
57         }
58         free(p);
59     }
60     else{ //p的左右子树均不为空 
61         pnode t = p;
62         pnode s = p->lchild;  //从p的左子节点开始 
63         while(s->rchild){  //找到p的前驱，即p左子树中值最大的节点 
64             t = s;   
65             s = s->rchild;    
66         }
67         p->val = s->val;   //把节点s的值赋给p 
68         if(t == p){
69             p->lchild = s->lchild;    
70         }    
71         else{
72             t->rchild = s->lchild;    
73         }
74         free(s); 
75     }
76     return find;
77 }

View Code

    查找操作：

 1 pnode search_BST(pnode p, int x)
 2 {
 3     bool solve = false;
 4     while(p && !solve){
 5         if(x == p->val){
 6             solve = true;    
 7         }    
 8         else if(x < p->val){
 9             p = p->lchild;    
10         }
11         else{
12             p = p->rchild;    
13         }
14     }
15     if(p == NULL){
16         cout << "没有找到" << x << endl;    
17     } 
18     return p;
19 }

View Code

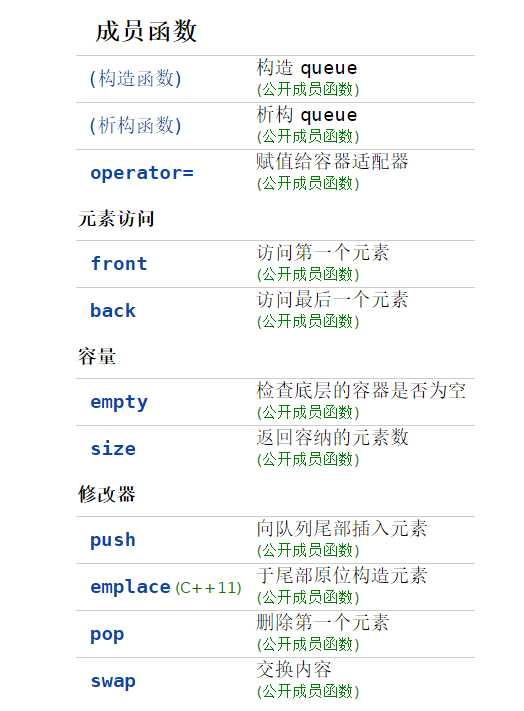
而在这次新学了queue头文件，在此网站，都是干货cppreference.com来玩呀！

 

而在深入虎穴中，数组越界问题真的是神魔啊

 1 int input(node *&a)
 2 {
 3     int x,n,i,j;
 4     bool *vi;
 5     cin >>n;
 6     a=new node[n+1];//为a数组申请空间 
 7     vi=new bool[n+1];//将vi数组初始化为false   
 8     for(i=1;i<=n;i++)
 9         vi[i] = false;
10         
11     for(i=1;i<=n;++i)
12     {
13         cin>>x;
14         a[i].doors=x;
15         a[i].p = new int[x];
16         for(j=0;j<x;++j){  //注意X下标问题
17              cin>>a[i].p[j];
18            vi[a[i].p[j]] =true;
19         }  
20     }
21     
22     //找出根在数组的下标 
23     for(i=1;i<=n;++i)
24        if (!vi[i]) break;       
25     return i;
26 }