数据结构——AVL数
Posted luanxm
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构——AVL数相关的知识,希望对你有一定的参考价值。
转自:http://www.cnblogs.com/skywang12345/p/3577479.html
AVL树的介绍
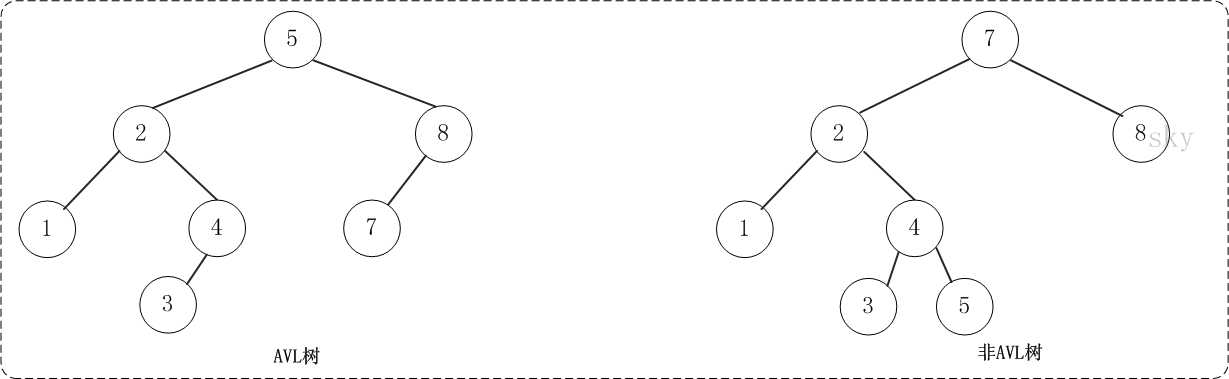
AVL树是高度平衡的而二叉树。它的特点是:AVL树中任何节点的两个子树的高度最大差别为1。
上面的两张图片,左边的是AVL树,它的任何节点的两个子树的高度差别都<=1;而右边的不是AVL树,因为7的两颗子树的高度相差为2(以2为根节点的树的高度是3,而以8为根节点的树的高度是1)。
AVL树的Java实现
1. 节点
1.1 节点定义
public class AVLTree<T> where T : IComparable<T> { private AVLTreeNode<T> mRoot;// 根结点 // AVL树的节点(内部类) public class AVLTreeNode<T> where T : IComparable<T> { public T key; public int height; public AVLTreeNode<T> left; public AVLTreeNode<T> right; public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) { this.key = key; this.left = left; this.right = right; this.height = 0; } } public AVLTree() { mRoot = null; }
AVLTree是AVL树对应的类,而AVLTreeNode是AVL树节点,它是AVLTree的内部类。AVLTree包含了AVL树的根节点,AVL树的基本操作也定义在AVL树中。AVLTreeNode包括的几个组成对象:
(01) key -- 是关键字,是用来对AVL树的节点进行排序的。
(02) left -- 是左孩子。
(03) right -- 是右孩子。
(04) height -- 是高度。
1.2 树的高度
/* * 获取树的高度 */ private int height(AVLTreeNode<T> tree) { if (tree != null) return tree.height; return 0; } public int height() { return height(mRoot); }
关于高度,有的地方将"空二叉树的高度是-1",而本文采用维基百科上的定义:树的高度为最大层次。即空的二叉树的高度是0,非空树的高度等于它的最大层次(根的层次为1,根的子节点为第2层,依次类推)。
1.3 比较大小
/* * 比较两个值的大小 */ private int max(int a, int b) { return a>b ? a : b; }
2. 旋转
如果在AVL树中进行插入或删除节点后,可能导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态:LL(左左),LR(左右),RR(右右)和RL(右左)。下面给出它们的示意图:
上图中的4棵树都是"失去平衡的AVL树",从左往右的情况依次是:LL、LR、RL、RR。除了上面的情况之外,还有其它的失去平衡的AVL树,如下图:
上面的两张图都是为了便于理解,而列举的关于"失去平衡的AVL树"的例子。总的来说,AVL树失去平衡时的情况一定是LL、LR、RL、RR这4种之一,它们都由各自的定义:
(1) LL:LeftLeft,也称为"左左"。插入或删除一个节点后,根节点的左子树的左子树还有非空子节点,导致"根的左子树的高度"比"根的右子树的高度"大2,导致AVL树失去了平衡。
例如,在上面LL情况中,由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点",而"根节点(8)的右子树(12)没有子节点";导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
(2) LR:LeftRight,也称为"左右"。插入或删除一个节点后,根节点的左子树的右子树还有非空子节点,导致"根的左子树的高度"比"根的右子树的高度"大2,导致AVL树失去了平衡。
例如,在上面LR情况中,由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点",而"根节点(8)的右子树(12)没有子节点";导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。
(3) RL:RightLeft,称为"右左"。插入或删除一个节点后,根节点的右子树的左子树还有非空子节点,导致"根的右子树的高度"比"根的左子树的高度"大2,导致AVL树失去了平衡。
例如,在上面RL情况中,由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点",而"根节点(8)的左子树(4)没有子节点";导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
(4) RR:RightRight,称为"右右"。插入或删除一个节点后,根节点的右子树的右子树还有非空子节点,导致"根的右子树的高度"比"根的左子树的高度"大2,导致AVL树失去了平衡。
例如,在上面RR情况中,由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点",而"根节点(8)的左子树(4)没有子节点";导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。
如果在AVL树中进行插入或删除节点后,可能导致AVL树失去平衡。AVL失去平衡之后,可以通过旋转使其恢复平衡,下面分别介绍"LL(左左),LR(左右),RR(右右)和RL(右左)"这4种情况对应的旋转方法。
2.1 LL的旋转
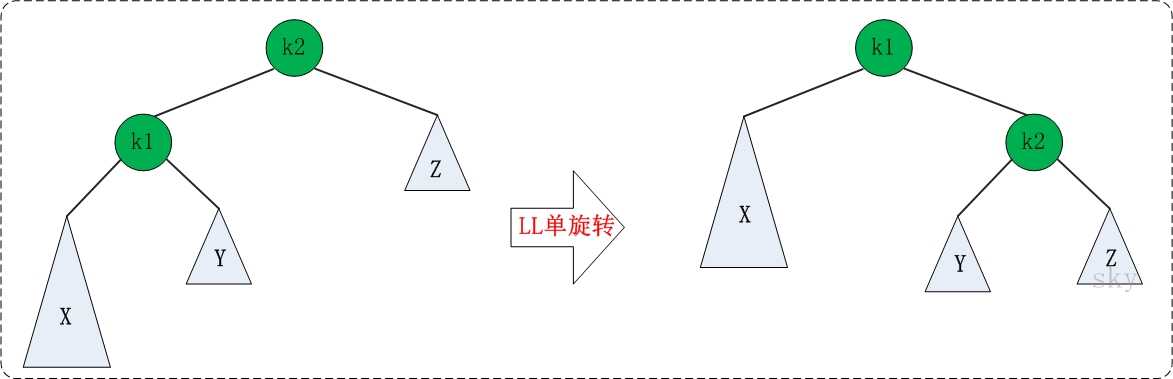
LL失去平衡的情况,可以通过一次旋转让AVL树恢复平衡。如下图:
图中左边是旋转之前的树,右边是旋转之后的树。从中可以发现,旋转之后的树又变成了AVL树,而且该旋转只需要一次即可完成。
对于LL旋转,你可以这样理解为:LL旋转是围绕"失去平衡的AVL根节点"进行的,也就是节点k2;而且由于是LL情况,即左左情况,就用手抓着"左孩子,即k1"使劲摇。将k1变成根节点,k2变成k1的右子树,"k1的右子树"变成"k2的左子树"。
LL的旋转代码
/* * LL:左左对应的情况(左单旋转)。 * * 返回值:旋转后的根节点 */ private AVLTreeNode<T> leftLeftRotation(AVLTreeNode<T> k2) { AVLTreeNode<T> k1; k1 = k2.left; k2.left = k1.right; k1.right = k2; k2.height = max( height(k2.left), height(k2.right)) + 1; k1.height = max( height(k1.left), k2.height) + 1; return k1; }
2.2 RR的旋转
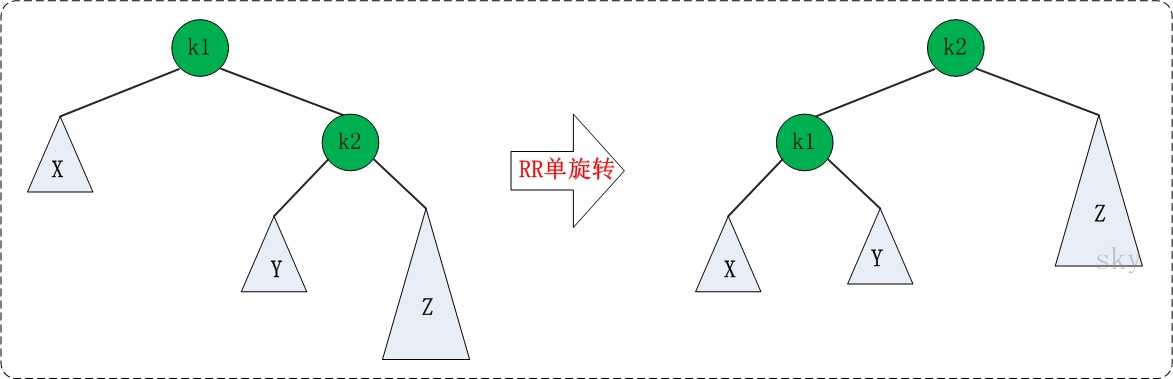
理解了LL之后,RR就相当容易理解了。RR是与LL对称的情况!RR恢复平衡的旋转方法如下:
图中左边是旋转之前的树,右边是旋转之后的树。RR旋转也只需要一次即可完成。
RR的旋转代码
/* * RR:右右对应的情况(右单旋转)。 * * 返回值:旋转后的根节点 */ private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k1) { AVLTreeNode<T> k2; k2 = k1.right; k1.right = k2.left; k2.left = k1; k1.height = max( height(k1.left), height(k1.right)) + 1; k2.height = max( height(k2.right), k1.height) + 1; return k2; }
2.3 LR的旋转
LR失去平衡的情况,需要经过两次旋转才能让AVL树恢复平衡。如下图:
第一次旋转是围绕"k1"进行的"RR旋转",第二次是围绕"k3"进行的"LL旋转"。
LR的旋转代码
/* * LR:左右对应的情况(左双旋转)。 * * 返回值:旋转后的根节点 */ private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> k3) { k3.left = rightRightRotation(k3.left); return leftLeftRotation(k3); }
2.4 RL的旋转
RL是与LR的对称情况!RL恢复平衡的旋转方法如下:
第一次旋转是围绕"k3"进行的"LL旋转",第二次是围绕"k1"进行的"RR旋转"。
RL的旋转代码
/* * RL:右左对应的情况(右双旋转)。 * * 返回值:旋转后的根节点 */ private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> k1) { k1.right = leftLeftRotation(k1.right); return rightRightRotation(k1); }
3. 插入
插入节点的代码
/* * 将结点插入到AVL树中,并返回根节点 * * 参数说明: * tree AVL树的根结点 * key 插入的结点的键值 * 返回值: * 根节点 */ private AVLTreeNode<T> insert(AVLTreeNode<T> tree, T key) { if (tree == null) { // 新建节点 tree = new AVLTreeNode<T>(key, null, null); if (tree == null) { Console.WriteLine("ERROR: create avltree node failed!"); return null; } } else { int cmp = key.CompareTo(tree.key); if (cmp < 0) { // 应该将key插入到"tree的左子树"的情况 tree.left = insert(tree.left, key); // 插入节点后,若AVL树失去平衡,则进行相应的调节。 if (height(tree.left) - height(tree.right) == 2) { if (key.CompareTo(tree.left.key) < 0) tree = leftLeftRotation(tree); else tree = leftRightRotation(tree); } } else if (cmp > 0) { // 应该将key插入到"tree的右子树"的情况 tree.right = insert(tree.right, key); // 插入节点后,若AVL树失去平衡,则进行相应的调节。 if (height(tree.right) - height(tree.left) == 2) { if (key.CompareTo(tree.right.key) > 0) tree = rightRightRotation(tree); else tree = rightLeftRotation(tree); } } else { // cmp==0 Console.WriteLine("添加失败:不允许添加相同的节点!"); } } tree.height = max(height(tree.left), height(tree.right)) + 1; return tree; } public void insert(T key) { mRoot = insert(mRoot, key); }
4. 删除
删除节点的代码
/* * 删除结点(z),返回根节点 * * 参数说明: * tree AVL树的根结点 * z 待删除的结点 * 返回值: * 根节点 */ private AVLTreeNode<T> remove(AVLTreeNode<T> tree, AVLTreeNode<T> z) { // 根为空 或者 没有要删除的节点,直接返回null。 if (tree == null || z == null) return null; int cmp = z.key.CompareTo(tree.key); if (cmp < 0) { // 待删除的节点在"tree的左子树"中 tree.left = remove(tree.left, z); // 删除节点后,若AVL树失去平衡,则进行相应的调节。 if (height(tree.right) - height(tree.left) == 2) { AVLTreeNode<T> r = tree.right; if (height(r.left) > height(r.right)) tree = rightLeftRotation(tree); else tree = rightRightRotation(tree); } } else if (cmp > 0) { // 待删除的节点在"tree的右子树"中 tree.right = remove(tree.right, z); // 删除节点后,若AVL树失去平衡,则进行相应的调节。 if (height(tree.left) - height(tree.right) == 2) { AVLTreeNode<T> l = tree.left; if (height(l.right) > height(l.left)) tree = leftRightRotation(tree); else tree = leftLeftRotation(tree); } } else { // tree是对应要删除的节点。 // tree的左右孩子都非空 if ((tree.left != null) && (tree.right != null)) { if (height(tree.left) > height(tree.right)) { // 如果tree的左子树比右子树高; // 则(01)找出tree的左子树中的最大节点 // (02)将该最大节点的值赋值给tree。 // (03)删除该最大节点。 // 这类似于用"tree的左子树中最大节点"做"tree"的替身; // 采用这种方式的好处是:删除"tree的左子树中最大节点"之后,AVL树仍然是平衡的。 AVLTreeNode<T> max = maximum(tree.left); tree.key = max.key; tree.left = remove(tree.left, max); } else { // 如果tree的左子树不比右子树高(即它们相等,或右子树比左子树高1) // 则(01)找出tree的右子树中的最小节点 // (02)将该最小节点的值赋值给tree。 // (03)删除该最小节点。 // 这类似于用"tree的右子树中最小节点"做"tree"的替身; // 采用这种方式的好处是:删除"tree的右子树中最小节点"之后,AVL树仍然是平衡的。 AVLTreeNode<T> min = maximum(tree.right); tree.key = min.key; tree.right = remove(tree.right, min); } } else { AVLTreeNode<T> tmp = tree; tree = (tree.left != null) ? tree.left : tree.right; tmp = null; } } return tree; } public void remove(T key) { AVLTreeNode<T> z; if ((z = search(mRoot, key)) != null) mRoot = remove(mRoot, z); }
完整的实现代码
/// <summary> /// AVL树 /// </summary> /// <typeparam name="T"></typeparam> public class AVLTree<T> where T : IComparable<T> { private AVLTreeNode<T> mRoot;// 根结点 // AVL树的节点(内部类) public class AVLTreeNode<T> where T : IComparable<T> { public T key; public int height; public AVLTreeNode<T> left; public AVLTreeNode<T> right; public AVLTreeNode(T key, AVLTreeNode<T> left, AVLTreeNode<T> right) { this.key = key; this.left = left; this.right = right; this.height = 0; } } public AVLTree() { mRoot = null; } /* * 获取树的高度 */ private int height(AVLTreeNode<T> tree) { if (tree != null) return tree.height; return 0; } public int height() { return height(mRoot); } /* * 比较两个值的大小 */ private int max(int a, int b) { return a > b ? a : b; } /* * 前序遍历"AVL树" */ private void preOrder(AVLTreeNode<T> tree) { if (tree != null) { Console.Write(tree.key + " "); preOrder(tree.left); preOrder(tree.right); } } public void preOrder() { preOrder(mRoot); } /* * 中序遍历"AVL树" */ private void inOrder(AVLTreeNode<T> tree) { if (tree != null) { inOrder(tree.left); Console.Write(tree.key + " "); inOrder(tree.right); } } public void inOrder() { inOrder(mRoot); } /* * 后序遍历"AVL树" */ private void postOrder(AVLTreeNode<T> tree) { if (tree != null) { postOrder(tree.left); postOrder(tree.right); Console.Write(tree.key + " "); } } public void postOrder() { postOrder(mRoot); } /* * (递归实现)查找"AVL树x"中键值为key的节点 */ private AVLTreeNode<T> search(AVLTreeNode<T> x, T key) { if (x == null) return x; int cmp = key.CompareTo(x.key); if (cmp < 0) return search(x.left, key); else if (cmp > 0) return search(x.right, key); else return x; } public AVLTreeNode<T> search(T key) { return search(mRoot, key); } /* * (非递归实现)查找"AVL树x"中键值为key的节点 */ private AVLTreeNode<T> IterativeSearch(AVLTreeNode<T> x, T key) { while (x != null) { int cmp = key.CompareTo(x.key); if (cmp < 0) x = x.left; else if (cmp > 0) x = x.right; else return x; } return x; } public AVLTreeNode<T> IterativeSearch(T key) { return IterativeSearch(mRoot, key); } /* * 查找最小结点:返回tree为根结点的AVL树的最小结点。 */ private AVLTreeNode<T> minimum(AVLTreeNode<T> tree) { if (tree == null) return null; while (tree.left != null) tree = tree.left; return tree; } public T minimum() { AVLTreeNode<T> p = minimum(mRoot); if (p != null) return p.key; return default(T); } /* * 查找最大结点:返回tree为根结点的AVL树的最大结点。 */ private AVLTreeNode<T> maximum(AVLTreeNode<T> tree) { if (tree == null) return null; while (tree.right != null) tree = tree.right; return tree; } public T maximum() { AVLTreeNode<T> p = maximum(mRoot); if (p != null) return p.key; return default(T); } /* * LL:左左对应的情况(左单旋转)。 * * 返回值:旋转后的根节点 */ private AVLTreeNode<T> leftLeftRotation(AVLTreeNode<T> k2) { AVLTreeNode<T> k1; k1 = k2.left; k2.left = k1.right; k1.right = k2; k2.height = max(height(k2.left), height(k2.right)) + 1; k1.height = max(height(k1.left), k2.height) + 1; return k1; } /* * RR:右右对应的情况(右单旋转)。 * * 返回值:旋转后的根节点 */ private AVLTreeNode<T> rightRightRotation(AVLTreeNode<T> k1) { AVLTreeNode<T> k2; k2 = k1.right; k1.right = k2.left; k2.left = k1; k1.height = max(height(k1.left), height(k1.right)) + 1; k2.height = max(height(k2.right), k1.height) + 1; return k2; } /* * LR:左右对应的情况(左双旋转)。 * * 返回值:旋转后的根节点 */ private AVLTreeNode<T> leftRightRotation(AVLTreeNode<T> k3) { k3.left = rightRightRotation(k3.left); return leftLeftRotation(k3); } /* * RL:右左对应的情况(右双旋转)。 * * 返回值:旋转后的根节点 */ private AVLTreeNode<T> rightLeftRotation(AVLTreeNode<T> k1) { k1.right = leftLeftRotation(k1.right); return rightRightRotation(k1); } /* * 将结点插入到AVL树中,并返回根节点 * * 参数说明: * tree AVL树的根结点 * key 插入的结点的键值 * 返回值: * 根节点 */ private AVLTreeNode<T> insert(AVLTreeNode<T> tree, T key) { if (tree == null) { // 新建节点 tree = new AVLTreeNode<T>(key, null, null); if (tree == null) { Console.WriteLine("ERROR: create avltree node failed!"); return null; } } else { int cmp = key.CompareTo(tree.key); if (cmp < 0) { // 应该将key插入到"tree的左子树"的情况 tree.left = insert(tree.left, key); // 插入节点后,若AVL树失去平衡,则进行相应的调节。 if (height(tree.left) - height(tree.right) == 2) { if (key.CompareTo(tree.left.key) < 0) tree = leftLeftRotation(tree); else tree = leftRightRotation(tree); } } else if (cmp > 0) { // 应该将key插入到"tree的右子树"的情况 tree.right = insert(tree.right, key); // 插入节点后,若AVL树失去平衡,则进行相应的调节。 if (height(tree.right) - height(tree.left) == 2) { if (key.CompareTo(tree.right.key) > 0) tree = rightRightRotation(tree); else tree = rightLeftRotation(tree); } } else { // cmp==0 Console.WriteLine("添加失败:不允许添加相同的节点!"); } } tree.height = max(height(tree.left), height(tree.right)) + 1; return tree; } public void insert(T key) { mRoot = insert(mRoot, key); } /* * 删除结点(z),返回根节点 * * 参数说明: * tree AVL树的根结点 * z 待删除的结点 * 返回值: * 根节点 */ private AVLTreeNode<T> remove(AVLTreeNode<T> tree, AVLTreeNode<T> z) { // 根为空 或者 没有要删除的节点,直接返回null。 if (tree == null || z == null) return null; int cmp = z.key.CompareTo(tree.key); if (cmp < 0) { // 待删除的节点在"tree的左子树"中 tree.left = remove(tree.left, z); // 删除节点后,若AVL树失去平衡,则进行相应的调节。 if (height(tree.right) - height(tree.left) == 2) { AVLTreeNode<T> r = tree.right; if (height(r.left) > height(r.right)) tree = rightLeftRotation(tree); else tree = rightRightRotation(tree); } } else if (cmp > 0) { // 待删除的节点在"tree的右子树"中 tree.right = remove(tree.right, z); // 删除节点后,若AVL树失去平衡,则进行相应的调节。 if (height(tree.left) - height(tree.right) == 2) { AVLTreeNode<T> l = tree.left; if (height(l.right) > height(l.left)) tree = leftRightRotation(tree); else tree = leftLeftRotation(tree); } } else { // tree是对应要删除的节点。 // tree的左右孩子都非空 if ((tree.left != null) && (tree.right != null)) { if (height(tree.left) > height(tree.right)) { // 如果tree的左子树比右子树高; // 则(01)找出tree的左子树中的最大节点 // (02)将该最大节点的值赋值给tree。 // (03)删除该最大节点。 // 这类似于用"tree的左子树中最大节点"做"tree"的替身; // 采用这种方式的好处是:删除"tree的左子树中最大节点"之后,AVL树仍然是平衡的。 AVLTreeNode<T> max = maximum(tree.left); tree.key = max.key; tree.left = remove(tree.left, max); } else { // 如果tree的左子树不比右子树高(即它们相等,或右子树比左子树高1) // 则(01)找出tree的右子树中的最小节点 // (02)将该最小节点的值赋值给tree。 // (03)删除该最小节点。 // 这类似于用"tree的右子树中最小节点"做"tree"的替身; // 采用这种方式的好处是:删除"tree的右子树中最小节点"之后,AVL树仍然是平衡的。 AVLTreeNode<T> min = maximum(tree.right); tree.key = min.key; tree.right = remove(tree.right, min); } } else { AVLTreeNode<T> tmp = tree; tree = (tree.left != null) ? tree.left : tree.right; tmp = null; } } return tree; } public void remove(T key) { AVLTreeNode<T> z; if ((z = search(mRoot, key)) != null) mRoot = remove(mRoot, z); } /* * 销毁AVL树 */ private void destroy(AVLTreeNode<T> tree) { if (tree == null) return; if (tree.left != null) destroy(tree.left); if (tree.right != null) destroy(tree.right); tree = null; } public void destroy() { destroy(mRoot); } /* * 打印"二叉查找树" * * key -- 节点的键值 * direction -- 0,表示该节点是根节点; * -1,表示该节点是它的父结点的左孩子; * 1,表示该节点是它的父结点的右孩子。 */ private void print(AVLTreeNode<T> tree, T key, int direction) { if (tree != null) { if (direction == 0) // tree是根节点 Console.WriteLine("{0} is root\\n", tree.key, key); else // tree是分支节点 Console.WriteLine("{0} is {1}‘s {2} child\\n", tree.key, key, direction == 1 ? "right" : "left"); print(tree.left, tree.key, -1); print(tree.right, tree.key, 1); } } public void print() { if (mRoot != null) print(mRoot, mRoot.key, 0); } }
AVL树的测试程序
public class AVLTreeTest { private int[] arr = { 3, 2, 1, 4, 5, 6, 7, 16, 15, 14, 13, 12, 11, 10, 8, 9 }; public void test() { int i; AVLTree<int> tree = new AVLTree<int>(); Console.WriteLine("== 依次添加: "); for (i = 0; i < arr.Length; i++) { Console.WriteLine("{0} ", arr[i]); tree.insert(arr[i]); } Console.WriteLine("\\n== 前序遍历: "); tree.preOrder(); Console.WriteLine("\\n== 中序遍历: "); tree.inOrder(); Console.WriteLine("\\n== 后序遍历: "); tree.postOrder(); Console.WriteLine("\\n"); Console.WriteLine("== 高度: {0}\\n", tree.height()); Console.WriteLine("== 最小值: {0}\\n", tree.minimum()); Console.WriteLine("== 最大值: {0}\\n", tree.maximum()); Console.WriteLine("== 树的详细信息: \\n"); tree.print(); i = 8; Console.WriteLine("\\n== 删除根节点: {0}", i); tree.remove(i); Console.WriteLine("\\n== 高度: {0}", tree.height()); Console.WriteLine("\\n== 中序遍历: "); tree.inOrder(); Console.WriteLine("\\n== 树的详细信息: \\n"); tree.print(); // 销毁二叉树 tree.destroy(); } }
AVL树的测试程序
结果如下:
== 依次添加: 3 2 1 4 5 6 7 16 15 14 13 12 11 10 8 9 == 前序遍历: 7 4 2 1 3 6 5 13 11 9 8 10 12 15 14 16 == 中序遍历: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 == 后序遍历: 1 3 2 5 6 4 8 10 9 12 11 14 16 15 13 7 == 高度: 5 == 最小值: 1 == 最大值: 16 == 树的详细信息: 7 is root 4 is 7‘s left child 2 is 4‘s left child 1 is 2‘s left child 3 is 2‘s right child 6 is 4‘s right child 5 is 6‘s left child 13 is 7‘s right child 11 is 13‘s left child 9 is 11‘s left child 8 is 9‘s left child 10 is 9‘s right child 12 is 11‘s right child 15 is 13‘s right child 14 is 15‘s left child 16 is 15‘s right child == 删除根节点: 8 == 高度: 5 == 中序遍历: 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16 == 树的详细信息: 7 is root 4 is 7‘s left child 2 is 4‘s left child 1 is 2‘s left child 3 is 2‘s right child 6 is 4‘s right child 5 is 6‘s left child 13 is 7‘s right child 11 is 13‘s left child 9 is 11‘s left child 10 is 9‘s right child 12 is 11‘s right child 15 is 13‘s right child 14 is 15‘s left child 16 is 15‘s right child
以上是关于数据结构——AVL数的主要内容,如果未能解决你的问题,请参考以下文章