反向传播BP算法

Posted 2021-11-27 wevolf

前向传播模型

一般我们使用的公式是：
\\[ a=\\frac{1}{1+\\exp \\left(-\\left(w^{T} x+b\\right)\\right)} = \\frac{1}{1+\\exp \\left(-\\left[w^{T} \\quad b\\right] \\cdot[x \\quad 1]\\right)} \\]
对于隐层有多个神经元的情况就是：
\\[ \\begin{array}{l}{a_{1}=\\frac{1}{1+\\exp \\left(w^{(1) T} x+b_{1}\\right)}} \\\\ {\\vdots} \\\\ {a_{m}=\\frac{1}{1+\\exp \\left(w^{(m) T} x+b_{m}\\right)}}\\end{array} \\]
记为：\\(z=W x+b\\)
\\[ \\left[ \\begin{array}{c}{a^{(1)}} \\\\ {\\vdots} \\\\ {a^{(m)}}\\end{array}\\right]=\\sigma(z)=\\sigma(W x+b) \\]

反向传播中的微积分计算

现在假设我们有一个三层神经网络，我们简单的表示成：
\\[ C\\left(w_{1}, b_{1}, w_{2}, b_{2}, w_{3}, b_{3}\\right) \\]
我们需要调整的就是这些变量，我们的目的就是希望这些变量作为参数，损失函数梯度下降的最快，

现在假设我们每层只有一个神经元，我们将神经网络最后一层得神经元用 \\(a^{(L)}\\)来表示，这一个损失函数我们可以表示成：\\(\\operatorname{cost} \\longrightarrow C_{0}(\\ldots)=\\left(a^{(L)}-y\\right)^{2}\\)

我们从倒数第二层 \\(a^{(L-1)}\\) 到 \\(a^{(L)}\\) 层的时候，由下面的公示的得到：
\\[ \\begin{aligned} z^{(L)} &=w^{(L)} a^{(L-1)}+b^{(L)} \\\\ a^{(L)} &=\\sigma\\left(z^{(L)}\\right) \\end{aligned} \\]
这个是前向传播的公式：现在我们想要损失函数下降的越快，那么 \\(C\\) 对 \\(w\\) 越敏感，下降得越快。这里我们将上面的求导用链式法则，只是简单的列出来，
\\[ \\frac{\\partial C_{0}}{\\partial w^{(L)}}=\\frac{\\partial z^{(L)}}{\\partial w^{(L)}} \\frac{\\partial a^{(L)}}{\\partial z^{(L)}} \\frac{\\partial C 0}{\\partial a^{(L)}} \\]
现在我们分别对上面公式后面的三个求导：
\\[ \\begin{aligned} \\frac{\\partial C_0}{\\partial a^{(L)}} &=2\\left(a^{(L)}-y\\right) \\\\ \\frac{\\partial a^{(L)}}{\\partial z^{(L)}} &=\\sigma^{\\prime}\\left(z^{(L)}\\right) \\\\ \\frac{\\partial z^{(L)}}{\\partial w^{(L)}} &=a^{(L-1)} \\end{aligned} \\]
然后我们得到下面的公式：
\\[ \\frac{\\partial C_{0}}{\\partial w^{(L)}}=\\frac{\\partial z^{(L)}}{\\partial w^{(L)}} \\frac{\\partial a^{(L)}}{\\partial z^{(L)}} \\frac{\\partial C _{0}}{\\partial a^{(L)}}=a^{(L-1)} \\sigma^{\\prime}\\left(z^{(L)}\\right) 2\\left(a^{(L)}-y\\right) \\]
对于这个式子，说明了梯度与哪些因素相关：由于上面的式子，我们只考虑了最终输出的一个元素，由于最后的网络输出的是一层，所以最后一层的神经元求得偏置应该是：
\\[ \\frac{\\partial C}{\\partial w^{(L)}}=\\frac{1}{n} \\sum_{k=0}^{n-1} \\frac{\\partial C_{k}}{\\partial w^{(L)}} \\]
上述只是对一个偏置 \\(w(L)\\) 求梯度，而我们要对所有的偏置求梯度，那就是：
\\[ \\nabla C=\\left[ \\begin{array}{c}{\\frac{\\partial C}{\\partial w^{(1)}}} \\\\ {\\frac{\\partial C}{\\partial b^{(1)}}} \\\\ {\\vdots} \\\\ {\\frac{\\partial C}{\\partial w^{(L)}}} \\\\ {\\frac{\\partial C}{\\partial b^{(L)}}}\\end{array}\\right] \\]

每层有多个神经元时

前面我们假设的是每层只有一个神经元，现在我们假设每层有多个神经元，我们表示神经网络如下：

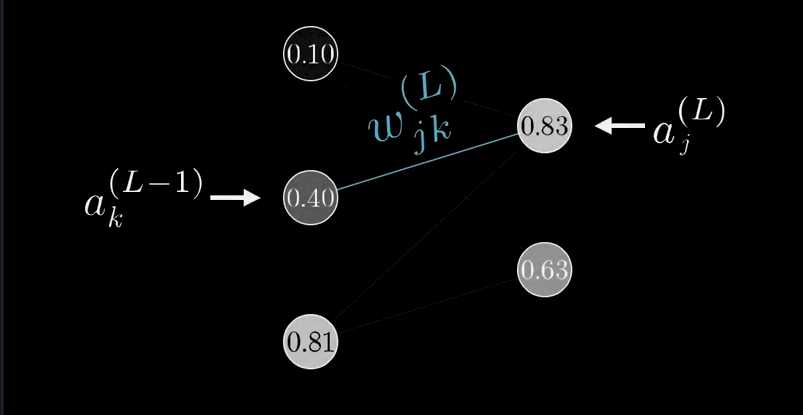
我们下一层的计算方法本质上是一样的：
\\[ z_{j}^{(L)}=w_{j 0}^{(L)} a_{0}^{(L-1)}+w_{j 1}^{(L)} a_{1}^{(L-1)}+w_{j 2}^{(L)} a_{2}^{(L-1)}+b_{j}^{(L)} \\]

\\[ a_{j}^{(L)}=\\sigma\\left(z_{j}^{(L)}\\right) \\]

上面的公式如果写成向量的形式，本质上与每层只有一个神经元是一样的。

此时我们的损失函数就是：
\\[ C_{0}=\\sum_{j=0}^{n_{L}-1}\\left(a_{j}^{(L)}-y_{j}\\right)^{2} \\]
损失函数对偏置求导：
\\[ \\frac{\\partial C_{0}}{\\partial w_{j k}^{(L)}}=\\frac{\\partial z_{j}^{(L)}}{\\partial w_{j k}^{(L)}} \\frac{\\partial a_{j}^{(L)}}{\\partial z_{j}^{(L)}} \\frac{\\partial C_{0}}{\\partial a_{j}^{(L)}} \\]
这个公式和每层只有一个神经元本质是一样的。

这里我们求的是最后一层，而反向传播的本质是要不断的向后，也就是从最后一层到倒数第二层，一直反向。上面我们求的是倒数第二层到最后一层的 \\(w_{j k}^{(L)}\\) 对最后一层损失函数的影响，那么再往后该怎么计算呢？所以我们要知道倒数第二层的期望值，所以我们用最后一层对倒数第二层求偏导：
\\[ \\frac{\\partial C_{0}}{\\partial a_{k}^{(L-1)}}=\\sum_{j=0}^{n_{L}-1} \\frac{\\partial z_{j}^{(L)}}{\\partial a_{k}^{(L-1)}} \\frac{\\partial a_{j}^{(L)}}{\\partial z_{j}^{(L)}} \\frac{\\partial C_{0}}{\\partial a_{j}^{(L)}} \\]
这样我们可以得到期望的 \\(a ^{(L-1)}\\), 也就算到了倒数第二层，然后我们再用这一层继续往后修正神经网络中的参数就可以了。

本质上就是，每一层的损失函数有三个参数：
\\[ \\begin{aligned} z^{(L)} &=w^{(L)} a^{(L-1)}+b^{(L)} \\\\ a^{(L)} &=\\sigma\\left(z^{(L)}\\right) \\end{aligned} \\]
分别是 \\(w^{(L)}\\) 和 \\(a^{(L-1)}\\) 以及$ b^{(L)}$. 所以我们对他们三个求偏导，也就是梯度下降求最优解来优化这三个参数。