ST表——————一失足成千古恨系列2

Posted 2021-11-27 lcez56jsy

在此先祝自己这个系列写的越少越好qwq（保证不超过4篇（flag已立））

考试原题：（绝壁是看完复联出的）

第一反应：线段树？？不对，是st表。嗯，没错。哎，st表咋写来着？？完了凉了。

结果：写暴搜的都有60分，结果我爆了0 qwq

           80-->0，与键盘无缘嘤嘤嘤

好了开始说正事

ST表用来干什么的？

给定一个区间，求最值。上面那道题是典型的模板题（虽然有毒瘤数据会卡掉st表，但我们这里不讨论）

复杂度：预处理：O(nlogn),询问：O(1)

先说预处理。

st表示一个二维数组，其中st[i][j]表示区间[i,i+2^j-1]中的最值，这里我们就拿最大值举例。显然st[i][0]=a[i],因为[i,i+1-1]中只有i一个点。那么我们怎么推其他的st[i][j]呢？

我们先来看一张图

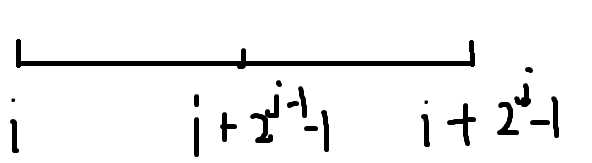
这样我们就可以推出来：st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]。为什么呢？因为i+2^(j-1)+2^(j-1)-1=i+2*(2^(j-1))-1=i+2^j-1

这样，我们就可以预处理出来所有的st[i][j]了

int st[maxn][23]//一般第二维不会超过20，这里是应对毒瘤数据范围
void init()
{
    for(int i=1;i<=n;i++)
        st[i][0]=a[i];
    for(int  i=1;(1<<i)<=n;i++)//这里实际上枚举上面说的j
    {for(int j=0;j+(1<<i)-1<n;j++)
       {st[j][i]=max(st[j][i-1],st[j+(1<<(i-1))][i-1]);//这里为什么j是第一维呢？这里我们max()里面变的只有第一维，所以我们要先处理第一维，才能保证后面正常进行（就是个顺序问题）
        }
    } 
}

查询给的区间可不是卡好2^k的，所以我们应该怎么查询呢？我们第二维表示的是i+2^j-1,我们看到这里有个次方，我们可以玄学的考虑一下log。（以2为底）

   这里区间的长度显然是2^j,我们已经考虑到log，那不妨对区间长度len=2^j来个log.（向下取整），设t=log(len)/log(2)向下取整，那么2^t一定<len/2。我们发现，l+2^t一定是在[l,r]的中间往右，而r-2^t一定在中间往左。[l,l+2^t-1]与[r-2^t+1,r]这两个区间是可以完全覆盖[l,r]，而且还不会有超出[l,r]的部分，所以我们就可以从st[l][t]和st[r-2^t+1][t]中选一个最大值。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;

int n,m,l,r,st[1<<20][20],a[1<<20];

int search(int l,int r)//查找
{  int t=log((double)(r-l+1))/log(2.0);
   return max(st[l][t],st[r-(1<<t)+1][t];
}
void init()//初始化
{
     for(int i=1;i<=n;i++)
     {for(int j=1;j+(1<<i)-1<=n;j++)
          {st[j][i]=max(st[j][i-1],st[j+(1<<(i-1))][i-1];
           }
      }
}
int main()
{
   scanf("%d%d",&n,&m);
   for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
   init();
   for(int i=1;i<=m;i++)
    {
          scanf("%d%d",&l,&r);
          printf("%d\\n",search(l,r));
    }
}