Brute-force Algorithm HDU - 3221（指数循环节 矩阵快速幂）

Posted 2021-11-27 wtsruvf

水题一道

推一下就是

f[n] = f[n - 1] + f[n - 2]

发现n很大

所以用矩阵快速幂就好了

还有P很大  那就指数循环节

一定要注意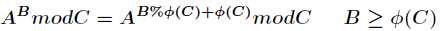   这个条件 

 

 

#include <iostream>
#include <cstdio>
#include <sstream>
#include <cstring>
#include <map>
#include <cctype>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <algorithm>
#include <list>
#include <cmath>
#include <bitset>
#define rap(i, a, n) for(int i=a; i<=n; i++)
#define rep(i, a, n) for(int i=a; i<n; i++)
#define lap(i, a, n) for(int i=n; i>=a; i--)
#define lep(i, a, n) for(int i=n; i>a; i--)
#define rd(a) scanf("%d", &a)
#define rlld(a) scanf("%lld", &a)
#define rc(a) scanf("%c", &a)
#define rs(a) scanf("%s", a)
#define rb(a) scanf("%lf", &a)
#define rf(a) scanf("%f", &a)
#define pd(a) printf("%d\\n", a)
#define plld(a) printf("%lld\\n", a)
#define pc(a) printf("%c\\n", a)
#define ps(a) printf("%s\\n", a)
#define MOD 2018
#define LL long long
#define ULL unsigned long long
#define Pair pair<int, int>
#define mem(a, b) memset(a, b, sizeof(a))
#define _  ios_base::sync_with_stdio(0),cin.tie(0)
//freopen("1.txt", "r", stdin);
using namespace std;
const int maxn = 1100000, INF = 0x7fffffff;

int prime[maxn+10], phi[maxn+10];
bool vis[maxn+10];
int ans;
LL P;
void get_phi()
{
    ans = 0;
    phi[1] = 1;
    for(int i=2; i<=maxn; i++)
    {
        if(!vis[i])
        {
            prime[++ans] = i;
            phi[i] = i - 1;
        }
        for(int j=1; j<=ans; j++)
        {
            if(i * prime[j] > maxn) break;
            vis[i * prime[j]] = 1;
            if(i % prime[j] == 0)
            {

                phi[i * prime[j]] = phi[i] * prime[j]; break;
            }
            else
                phi[i * prime[j]] = phi[i] * (prime[j] - 1);
        }
    }
}

LL q_pow(LL a, LL b)
{
    LL res = 1;
    while(b)
    {
        if(b & 1) res = res * a % P;
        a = a * a % P;
        b >>= 1;
    }
    return res;
}
int tot;
struct Matrix
{
    LL v[110][110];
    Matrix()
    {
        memset(v, 0, sizeof(v));
    }
    Matrix operator *(const Matrix B)    // 重载的速度比写独立的函数慢点。
    {
        int i, j, k;
        Matrix C;
        for(i = 0; i <= tot; i ++)
            for(j = 0; j <= tot; j ++)
                for(k = 0; k <= tot; k ++)
                {
                    C.v[i][j] = (C.v[i][j] + v[i][k] * B.v[k][j]) % phi[P];

                }
        return C;
    }
};

Matrix mtPow(Matrix A, LL k)           // 用位运算代替递归求 A^k。
{
    int i;
    Matrix B;
    for(i = 0; i <= tot; i ++)
    {
        B.v[i][i] = 1;
    }
    while(k)
    {
        if(k & 1) B = B * A;
        A = A * A;
        k >>= 1;
    }
    return B;
}


int main()
{
    get_phi();
    int kase = 0;

    int T;
    rd(T);
    while(T--)
    {
        tot = 1;
        LL a, b, n;
        cin >> a >> b >> P >> n;
        if(n == 1)
            printf("Case #%d: %lld\\n", ++kase, a % P);
        else if(n == 2)
            printf("Case #%d: %lld\\n", ++kase, b % P);
        else if(n == 3)
            printf("Case #%d: %lld\\n", ++kase, a * b % P);
        else
        {
            Matrix A, B;
            A.v[0][0] = A.v[0][1] = A.v[1][0] = 1;
            A.v[1][1] = 0;
            B = mtPow(A, n - 3);
            LL d1 = B.v[0][0] + B.v[0][1], d2 = B.v[1][0] + B.v[1][1];
            if(d2 >= phi[P]) d2 = d2 % phi[P] + phi[P];
            if(d1 >= phi[P]) d1 = d1 % phi[P] + phi[P];
            a = q_pow(a, d2) % P;
            b = q_pow(b, d1) % P;
            printf("Case #%d: ", ++kase);
            cout << a * b % P << endl;
        }

    }

    return 0;
}