数据结构学习总结 线性表之单链表
Posted 2019wxw
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构学习总结 线性表之单链表相关的知识,希望对你有一定的参考价值。
一,回忆链表
链表,别名链式存储结构或单链表,用于存储逻辑关系为 "一对一" 的数据。与顺序表不同,链表不限制数据的物理存储状态,换句话说,使用链表存储的数据元素,其物理存储位置是随机的。
例如,使用链表存储 {1,2,3},数据的物理存储状态如图 1 所示:

图 1 链表随机存储数据
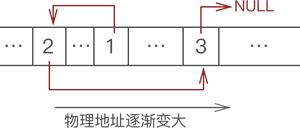
图 2 各数据元素配备指针
像图 2 这样,数据元素随机存储,并通过指针表示数据之间逻辑关系的存储结构就是链式存储结构。
链表的节点
从图 2 可以看到,链表中每个数据的存储都由以下两部分组成:
- 数据元素本身,其所在的区域称为数据域;
- 指向直接后继元素的指针,所在的区域称为指针域;
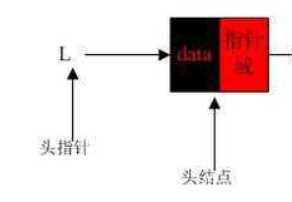
即链表中存储各数据元素的结构如图 3 所示:

图 3 节点结构

图 4 链表中的节点
typedef struct Link{ char elem; //代表数据域 struct Link * next; //代表指针域,指向直接后继元素 }link; //link为节点名,每个节点都是一个 link 结构体
提示,由于指针域中的指针要指向的也是一个节点,因此要声明为 Link 类型(这里要写成 struct Link* 的形式)。
头节点,头指针,和首元节点
其实,图 4 所示的链表结构并不完整。一个完整的链表需要由以下几部分构成:
- 头指针:一个普通的指针,它的特点是永远指向链表第一个节点的位置。很明显,头指针用于指明链表的位置,便于后期找到链表并使用表中的数据;
- 节点:链表中的节点又细分为头节点、首元节点和其他节点:
- 头节点:其实就是一个不存任何数据的空节点,通常作为链表的第一个节点。对于链表来说,头节点不是必须的,它的作用只是为了方便解决某些实际问题;
- 首元节点:由于头节点(也就是空节点)的缘故,链表中称第一个存有数据的节点为首元节点。首元节点只是对链表中第一个存有数据节点的一个称谓,没有实际意义;
- 其他节点:链表中其他的节点;
注意:关于头指针P:分为指针p空间和指针p所指向的空间;
理解:前面定义指针变量p并分配所指向空间的语句(link*)malloc(sizeof(link));部分是由计算机分配一个没有名字的内存空间,通过将其首地址放到变量p中,程序员就可以用变量p间接的操作这块空间,为简化,通常不画出p变量的空间,故可以表示为如下:
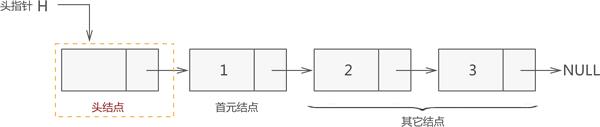
因此,一个存储 {1,2,3} 的完整链表结构如图 5 所示:
注意:链表中有头节点时,头指针指向头节点;反之,若链表中没有头节点,则头指针指向首元节点。
链表的创建(初始化)
创建一个链表需要做如下工作:
- 声明一个头指针(如果有必要,可以声明一个头节点);
- 创建多个存储数据的节点,在创建的过程中,要随时与其前驱节点建立逻辑关系;
例如,创建一个存储 {1,2,3,4} 且无头节点的链表,C 语言实现代码如下:
link * initLink(){ link * p=NULL;//创建头指针 link * temp = (link*)malloc(sizeof(link));//创建首元节点 //首元节点先初始化 temp->elem = 1; temp->next = NULL; p = temp;//头指针指向首元节点 //从第二个节点开始创建 for (int i=2; i<5; i++) { //创建一个新节点并初始化 link *a=(link*)malloc(sizeof(link)); a->elem=i; a->next=NULL; //将temp节点与新建立的a节点建立逻辑关系 temp->next=a; //指针temp每次都指向新链表的最后一个节点,其实就是 a节点,这里写temp=a也对 temp=temp->next; } //返回建立的节点,只返回头指针 p即可,通过头指针即可找到整个链表 return p; }
如果想创建一个存储 {1,2,3,4} 且含头节点的链表,则 C 语言实现代码为:
link * initLink(){ link * p=(link*)malloc(sizeof(link));//创建一个头结点 link * temp=p;//声明一个指针指向头结点, //生成链表 for (int i=1; i<5; i++) { link *a=(link*)malloc(sizeof(link)); a->elem=i; a->next=NULL; temp->next=a; temp=temp->next; } return p;
如果使用带有头节点创建链表的方式,则输出链表的 display 函数需要做适当地修改:
void display(link *p){ link* temp=p;//将temp指针重新指向头结点 //只要temp指针指向的结点的next不是Null,就执行输出语句。 while (temp->next) { temp=temp->next; printf("%d",temp->elem); } printf("\\n"); }
我们只需在主函数中调用 initLink 函数,即可轻松创建一个存储 {1,2,3,4} 的链表,C 语言完整代码如下:

#include<stdlib.h> #include<stdio.h> //定义链表结构 typedef struct link { int elem;//数据域 link *next;//指针域,指向直接后继元素 }link;//link为节点名,每个节点都是一个link结构体 //初始化无头节点链表函数 link* initNoToplink(); //创建有头节点的初始化链表 link * initlink(); //用于输出链表函数无头节点 void display(link *p); void havadisplay(link *p); int main() { //初始化链表{1,2,3,4} printf("初始化链表为无头节点:\\n"); link *p = initNoToplink(); display(p); printf("初始化链表为有头节点:\\n"); p = initlink(); havadisplay(p); return 0; } void havadisplay(link *p) { link* temp = p;//将temp指针重新指向头结点 //只要temp指针指向的结点的next不是Null,就执行输出语句。 while (temp->next) { temp = temp->next; printf("%d ", temp->elem); } printf("\\n"); } //无头节点遍历链表 void display(link *p) { link *temp = p;//将temp指针重新指向头节点 //判断只要temp指针指向的节点next不是null,就执行输出语句 while (temp) { printf("%d ",temp->elem); temp = temp->next; } printf("\\n"); } //有头节点初始化 link * initlink() { link * p = (link*)malloc(sizeof(link));//创建一个头结点 link * temp = p;//声明一个指针指向头结点, //生成链表 for (int i = 1; i<5; i++) { link *a = (link*)malloc(sizeof(link)); a->elem = i; a->next = NULL; temp->next = a; temp = temp->next; } return p; } //无头节点初始化 link *initNoToplink() { link *p=NULL;//创建头指针 link *temp = (link*)malloc(sizeof(link));//创建首元节点 //初始化首元节点 temp->elem = 1; temp->next = NULL; p = temp;//头指针指向首元节点 //从第二个节点开始创建 for (int i = 2; i < 5;i++) { link *a = (link*)malloc(sizeof(link));//创建一个新的节点并初始化 a->elem = i; a->next = NULL; temp->next = a;//将temp节点与新建立的a节点建立逻辑关系 //指针temp每次指向新链表的最后一个节点,其实就是a节点,这里temp=a;也对 temp = temp->next; } return p; }
运行结果为

链表的基本操作
以下对链表的操作实现均建立在已创建好链表的基础上,创建链表的代码如下所示
//声明节点结构 typedef struct Link{ int elem;//存储整形元素 struct Link *next;//指向直接后继元素的指针 }link; //创建链表的函数 link * initLink(){ link * p=(link*)malloc(sizeof(link));//创建一个头结点 link * temp=p;//声明一个指针指向头结点,用于遍历链表 //生成链表 for (int i=1; i<5; i++) { //创建节点并初始化 link *a=(link*)malloc(sizeof(link)); a->elem=i; a->next=NULL; //建立新节点与直接前驱节点的逻辑关系 temp->next=a; temp=temp->next; } return p; }
从实现代码中可以看到,该链表是一个具有头节点的链表。由于头节点本身不用于存储数据,因此在实现对链表中数据的"增删查改"时要引起注意。
链表插入元素
同顺序表一样,向链表中增添元素,根据添加位置不同,可分为以下 3 种情况:
- 插入到链表的头部(头节点之后),作为首元节点;
- 插入到链表中间的某个位置;
- 插入到链表的最末端,作为链表中最后一个数据元素;
虽然新元素的插入位置不固定,但是链表插入元素的思想是固定的,只需做以下两步操作,即可将新元素插入到指定的位置:
- 将新结点的 next 指针指向插入位置后的结点;
- 将插入位置前结点的 next 指针指向插入结点;
例如,我们在链表 {1,2,3,4} 的基础上分别实现在头部、中间部位、尾部插入新元素 5,其实现过程如图 1 所示:
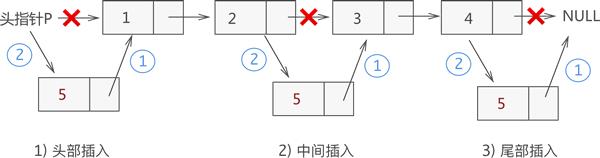
图 1 链表中插入元素的 3 种情况示意图
从图中可以看出,虽然新元素的插入位置不同,但实现插入操作的方法是一致的,都是先执行步骤 1 ,再执行步骤 2。
注意:链表插入元素的操作必须是先步骤 1,再步骤 2;反之,若先执行步骤 2,会导致插入位置后续的部分链表丢失,无法再实现步骤 1。
通过以上的讲解,我们可以尝试编写 C 语言代码来实现链表插入元素的操作:
//p为原链表,elem表示新数据元素,add表示新元素要插入的位置 link * insertElem(link * p,int elem,int add){ link * temp=p;//创建临时结点temp //首先找到要插入位置的上一个结点 for (int i=1; i<add; i++) { if (temp==NULL) { printf("插入位置无效\\n"); return p; } temp=temp->next; } //创建插入结点c link * c=(link*)malloc(sizeof(link)); c->elem=elem; //向链表中插入结点 c->next=temp->next; temp->next=c; return p; }
提示,insertElem 函数中加入一个 if 语句,用于判断用户输入的插入位置是否有效。例如,在已存储 {1,2,3} 的链表中,用户要求在链表中第 100 个数据元素所在的位置插入新元素,显然用户操作无效,此时就会触发 if 语句。
链表删除元素
从链表中删除指定数据元素时,实则就是将存有该数据元素的节点从链表中摘除,但作为一名合格的程序员,要对存储空间负责,对不再利用的存储空间要及时释放。因此,从链表中删除数据元素需要进行以下 2 步操作:
- 将结点从链表中摘下来;
- 手动释放掉结点,回收被结点占用的存储空间;
其中,从链表上摘除某节点的实现非常简单,只需找到该节点的直接前驱节点 temp,执行一行程序:
temp->next=temp->next->next;
例如,从存有 {1,2,3,4} 的链表中删除元素 3,则此代码的执行效果如图 2 所示:

图 2 链表删除元素示意图
因此,链表删除元素的 C 语言实现如下所示:
//p为原链表,add为要删除元素的值 link * delElem(link * p,int add){ link * temp=p; //temp指向被删除结点的上一个结点 for (int i=1; i<add; i++) { temp=temp->next; } link * del=temp->next;//单独设置一个指针指向被删除结点,以防丢失 temp->next=temp->next->next;//删除某个结点的方法就是更改前一个结点的指针域 free(del);//手动释放该结点,防止内存泄漏 return p; }
我们可以看到,从链表上摘下的节点 del 最终通过 free 函数进行了手动释放。
链表查找元素
在链表中查找指定数据元素,最常用的方法是:从表头依次遍历表中节点,用被查找元素与各节点数据域中存储的数据元素进行比对,直至比对成功或遍历至链表最末端的 NULL(比对失败的标志)。
因此,链表中查找特定数据元素的 C 语言实现代码为:
//p为原链表,elem表示被查找元素、 int selectElem(link * p,int elem){ //新建一个指针t,初始化为头指针 p link * t=p; int i=1; //由于头节点的存在,因此while中的判断为t->next while (t->next) { t=t->next; if (t->elem==elem) { return i; } i++; } //程序执行至此处,表示查找失败 return -1; }
注意,遍历有头节点的链表时,需避免头节点对测试数据的影响,因此在遍历链表时,建立使用上面代码中的遍历方法,直接越过头节点对链表进行有效遍历。
链表更新元素
更新链表中的元素,只需通过遍历找到存储此元素的节点,对节点中的数据域做更改操作即可。
直接给出链表中更新数据元素的 C 语言实现代码:
//更新函数,其中,add 表示更改结点在链表中的位置,newElem 为新的数据域的值 link *amendElem(link * p,int add,int newElem){ link * temp=p; temp=temp->next;//在遍历之前,temp指向首元结点 //遍历到被删除结点 for (int i=1; i<add; i++) { temp=temp->next; } temp->elem=newElem; return p; }
总结
以上内容详细介绍了对链表中数据元素做"增删查改"的实现过程及 C 语言代码,在此给出本节的完整可运行代码:

#include<stdio.h> #include<stdlib.h> //声明节点结构 typedef struct Link { int elem;//存储整型元素 struct Link *next;//指向直接后继元素的指针 }Link; //创建一个带头结点的函数 Link* initLink() { Link *p = (Link*)malloc(sizeof(Link));//创建一个头节点 Link *temp = p;//声明一个指针指向头节点,用于遍历链表 //生成链表 for (int i = 1; i < 5;i++) { //创建节点并初始化 Link* a = (Link*)malloc(sizeof(Link)); a->elem = i; a->next = NULL; //建立新节点与直接前驱节点的关系 temp->next = a; //指针temp每次都指向新链表的最后一个节点,其实就是 a节点,这里写temp=a也对 temp = temp->next; } return p; } //插入元素 //p为原链表,elem为插入的新数据元素 add为插入节点的位置 Link* InsertLink(Link *p,int elem,int add) { Link* temp = p;//创建临时节点temp //首先找到要插入位置的上一个节点 for (int i = 1; i < add;i++) { if (temp==NULL) { printf("插入位置无效\\n"); return p; } temp = temp->next; } //创建插入的节点C Link *c = (Link*)malloc(sizeof(Link)); c->elem = elem; //向链表中插入节点 c->next = temp->next;//先断后 temp->next = c;//再断前 return p; } //链表的删除 //p为原链表,add为要删除链表的值 Link* delLink(Link *p,int add) { Link* temp = p;//创建一个临时节点 //temp指向被删除节点的上一个节点 for (int i = 1; i < add;i++) { temp = temp->next; } Link *del = temp->next;//单独设置一个指针指向被删除节点,以防丢失 temp->next = temp->next->next;//删除某个节点的方法是更改前一个节点的指针域 free(del);//手动释放该节点防止内存泄漏 return p; } //链表查找 //p为原链表,elem表示被查找元素 int selectElem(Link* p,int elem) { //新建一个临时指针,初始化为头指针p Link* t = p; int i = 1; //由于头节点的存在,因此while中的判断为t->next; while (t->next) { t = t->next; if (t->elem==elem) { return i; } i++; } //程序执行至此,表示查找失败 printf("查找元素不存在"); return -1; } //更新链表 //p表示原链表,add更改节点在链表中的位置,newElem为新的元素 Link* updataLink(Link* p,int add,int newElem) { Link* temp = p;//建立临时节点 //遍历之前,temp指向首元节点 temp = temp->next; //遍历到被删除的节点 for (int i = 1; i < add;i++) { temp = temp->next; } temp->elem = newElem; return p; } //遍历有头节点的链表 void display(Link *p) { Link* temp = p;//将temp指针重新指向头结点 //只要temp指针指向的结点的next不是Null,就执行输出语句。 while (temp->next) { temp = temp->next; printf("%d ", temp->elem); } printf("\\n"); } int main() { //初始化链表(1,2,3,4) printf("初始化链表为:\\n"); Link *p = initLink(); display(p); printf("在第4的位置插入元素5:\\n"); p = InsertLink(p, 5, 4); display(p); printf("删除元素3:\\n"); p = delLink(p, 3); display(p); printf("查找元素2的位置为:\\n"); int address = selectElem(p, 2); if (address == -1) { printf("没有该元素\\n"); } else { printf("元素2的位置为:%d \\n", address); } printf("更改第3的位置上的数据为7:\\n"); p = updataLink(p, 3, 7); display(p); return 0; }
链表与顺序表的优缺点
原理:顺序表存储是将数据元素放到一块连续的内存存储空间,相邻数据元素的存放地址也相邻(逻辑与物理统一)。
优点:(1)空间利用率高。(局部性原理,连续存放,命中率高)
(2)存取速度高效,通过下标来直接存储。
缺点:(1)插入和删除比较慢,比如:插入或者删除一个元素时,整个表需要遍历移动元素来重新排一次顺序。
(2)不可以增长长度,有空间限制,当需要存取的元素个数可能多于顺序表的元素个数时,会出现"溢出"问题.当元素个数远少于预先分配的空间时,空间浪费巨大。
时间性能 :查找 O(1) ,插入和删除O(n)。
2.链表存储
原理:链表存储是在程序运行过程中动态的分配空间,只要存储器还有空间,就不会发生存储溢出问题,相邻数据元素可随意存放,但所占存储空间分两部分,一部分存放结点值,另一部分存放表示结点关系间的指针。
优点:(1) 存取某个元素速度慢。
(2)插入和删除速度快,保留原有的物理顺序,比如:插入或者删除一个元素时,只需要改变指针指向即可。
(3)没有空间限制,存储元素的个数无上限,基本只与内存空间大小有关.
缺点:(1)占用额外的空间以存储指针(浪费空间,不连续存放,malloc开辟,空间碎片多)
(2)查找速度慢,因为查找时,需要循环链表访问,需要从开始节点一个一个节点去查找元素访问。
时间性能 :查找 O(n) ,插入和删除O(1)。
*频繁的查找却很少的插入和删除操作可以用顺序表存储,堆排序,二分查找适宜用顺序表.
*如果频繁的插入和删除操作很少的查询就可以使用链表存储
*顺序表适宜于做查找这样的静态操作;链表适宜于做插入、删除这样的动态操作。
*若线性表长度变化不大,如果事先知道线性表的大致长度,比如一年12月,一周就是星期一至星期日共七天,且其主要操作是查找,则采用顺序表;若线性表长度变化较大或根本不知道多大时,且其主要操作是插入、删除,则采用链表,这样可以不需要考虑存储空间的大小问题。
链式:随机存储,顺序读取(必须遍历)
静态链表
例如,使用静态链表存储
{1,2,3} 的过程如下:创建一个足够大的数组,假设大小为 6,如图 1 所示

图 1 空数组
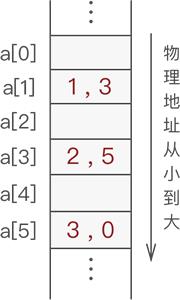
图 2 静态链表存储数据
通常,静态链表会将第一个数据元素放到数组下标为 1 的位置(a[1])中。
类似图 2 这样,通过 "数组+游标" 的方式存储具有线性关系数据的存储结构就是静态链表。
静态链表中的节点
通过上面的学习我们知道,静态链表存储数据元素也需要自定义数据类型,至少需要包含以下 2 部分信息:- 数据域:用于存储数据元素的值;
- 游标:其实就是数组下标,表示直接后继元素所在数组中的位置;
typedef struct { int data;//数据域 int cur;//游标 }component;
备用链表
图 2 显示的静态链表还不够完整,静态链表中,除了数据本身通过游标组成的链表外,还需要有一条连接各个空闲位置的链表,称为备用链表。
备用链表的作用是回收数组中未使用或之前使用过(目前未使用)的存储空间,留待后期使用。也就是说,静态链表使用数组申请的物理空间中,存有两个链表,一条连接数据,另一条连接数组中未使用的空间。
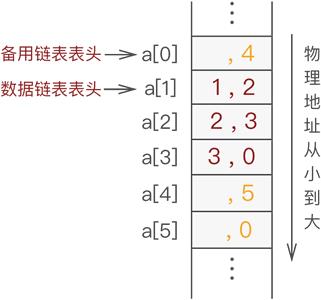
通常,备用链表的表头位于数组下标为 0(a[0]) 的位置,而数据链表的表头位于数组下标为 1(a[1])的位置。
{1,2,3},假设使用长度为 6 的数组 a,则存储状态可能如图 3 所示: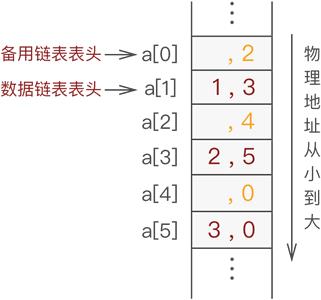

图 4 未存储数据之前静态链表的状态
图 3 备用链表和数据链表
静态链表的实现
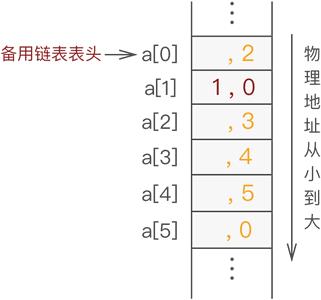
假设使用静态链表(数组长度为 6)存储{1,2,3},则需经历以下几个阶段。在数据链表未初始化之前,数组中所有位置都处于空闲状态,因此都应被链接在备用链表上,如图 4 所示:
备用链表摘除节点最简单的方法是摘除 a[0] 的直接后继节点;同样,向备用链表中添加空闲节点也是添加作为 a[0] 新的直接后继节点。因为 a[0] 是备用链表的第一个节点,我们知道它的位置,操作它的直接后继节点相对容易,无需遍历备用链表,耗费的时间复杂度为O(1)。
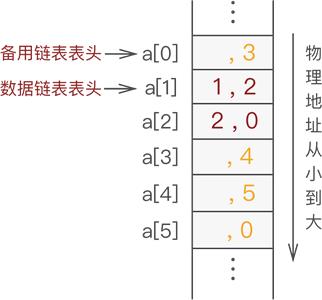
下面给出了创建静态链表的 C 语言实现代码:

#include<stdlib.h> #include<stdio.h> #define maxSize 6 typedef struct { int data;//数据域 int cur;//指针域 }component; //将结构体数据中所有分量连接到备用链表 void reserveArr(component* array); //初始化静态链表 int initArr(component* array); //输出函数 void displayArr(component*,int body); //从备用链表上摘下空闲节点的函数 int mallocArr(component* array); int main() { component array[maxSize]; int body = initArr(array); printf("静态链表为:\\n"); displayArr(array, body); return 0; } //创建备用链表 void reserveArr(component* array) { for (int i = 0; i < maxSize;i++) { array[i].cur = i + 1;//将每个数组分量链接到一起 } array[maxSize - 1].cur = 0;//链表最后一个节点的游标值为0 } //提取分配空间 int mallocArr(component* array) { //若备用链表非空,则返回分配的节点下标,否则返回0 //(当分配最后一个节点时,该节点的游标值为0) int i = array[0].cur; if (array[0].cur) { array[0].cur = array[i].cur; } return i; } //初始化静态链表 int initArr(component *array) { reserveArr(array); int body = mallocArr(array); //声明一个变量,把它当指针使,指向链表的最后的一个结点,因为链表为空,所以和头结点重合 int tempBody = body; for (int i = 1; i<4; i++) { int j = mallocArr(array);//从备用链表中拿出空闲的分量 array[tempBody].cur = j;//将申请的空闲分量链接在链表的最后一个结点后面 array[j].data = i;//给新申请的分量的数据域初始化 tempBody = j;//将指向链表最后一个结点的指针后移 } array[tempBody].cur = 0;//新的链表最后一个结点的指针设置为0 return body; } void displayArr(component * array, int body) { int tempBody = body;//tempBody准备做遍历使用 while (array[tempBody].cur) { printf("%d,%d ", array[tempBody].data, array[tempBody].cur); tempBody = array[tempBody].cur; } printf("%d,%d\\n", array[tempBody].data, array[tempBody].cur); }

提示,此代码创建了一个带有头节点的静态链表,因此最先输出的 ",2" 表示的是头节点,其首元节点(存储元素 1 的节点)在数组 array[2] 中。
双向链表

循环链表实现约瑟夫环
约瑟夫环问题,是一个经典的循环链表问题,题意是:已知 n 个人(分别用编号 1,2,3,…,n 表示)围坐在一张圆桌周围,从编号为 k 的人开始顺时针报数,数到 m 的那个人出列;他的下一个人又从 1 开始,还是顺时针开始报数,数到 m 的那个人又出列;依次重复下去,直到圆桌上剩余一个人。如图 2 所示,假设此时圆周周围有 5 个人,要求从编号为 3 的人开始顺时针数数,数到 2 的那个人出列:
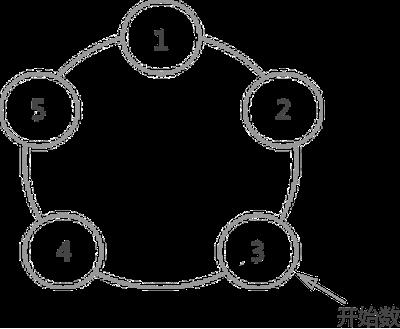
图 2 循环链表实现约瑟夫环
- 编号为 3 的人开始数 1,然后 4 数 2,所以 4 先出列;
- 4 出列后,从 5 开始数 1,1 数 2,所以 1 出列;
- 1 出列后,从 2 开始数 1,3 数 2,所以 3 出列;
- 3 出列后,从 5 开始数 1,2 数 2,所以 2 出列;
- 最后只剩下 5 自己,所以 5 胜出。
约瑟夫环问题有多种变形,比如顺时针转改为逆时针等,虽然问题的细节有多种变数,但解决问题的中心思想是一样的,即使用循环链表。

#include <stdio.h> #include <stdlib.h> typedef struct node{ int number; struct node * next; }person; person * initLink(int n){ person * head=(person*)malloc(sizeof(person)); head->number=1; head->next=NULL; person * cyclic=head; for (int i=2; i<=n; i++) { person * body=(person*)malloc(sizeof(person)); body->number=i; body->next=NULL; cyclic->next=body; cyclic=cyclic->next; } cyclic->next=head;//首尾相连 return head; } void findAndKillK(person * head,int k,int m){ person * tail=head; //找到链表第一个结点的上一个结点,为删除操作做准备 while (tail->next!=head) { tail=tail->next; } person * p=head; //找到编号为k的人 while (p->number!=k) { tail=p; p=p->next; } //从编号为k的人开始,只有符合p->next==p时,说明链表中除了p结点,所有编号都出列了, while (p->next!=p) { //找到从p报数1开始,报m的人,并且还要知道数m-1de人的位置tail,方便做删除操作。 for (int i=1; i<m; i++) { tail=p; p=p->next; } tail->next=p->next;//从链表上将p结点摘下来 printf("出列人的编号为:%d\\n",p->number); free(p); p=tail->next;//继续使用p指针指向出列编号的下一个编号,游戏继续 } printf("出列人的编号为:%d\\n",p->number); free(p); } int main() { printf("输入圆桌上的人数n:"); int n; scanf("%d",&n); person * head=initLink(n); printf("从第k人开始报数(k>1且k<%d):",n); int k; scanf("%d",&k); printf("数到m的人出列:"); int m; scanf("%d",&m); findAndKillK(head, k, m); return 0; }
输出:

最后出列的人,即为胜利者。当然,你也可以改进程序,令查找出最后一个人时,输出此人胜利的信息。
总结
循环链表和动态链表唯一不同在于它的首尾连接,这也注定了在使用循环链表时,附带最多的操作就是遍历链表。
在遍历的过程中,尤其要注意循环链表虽然首尾相连,但并不表示该链表没有第一个节点和最后一个结点。所以,不要随意改变头指针的指向。
以上是关于数据结构学习总结 线性表之单链表的主要内容,如果未能解决你的问题,请参考以下文章