第五章学习小结

Posted 2021-11-26 xiedehan

---恢复内容开始---

第五章主要学习的是树与二叉树，有利用数组进行存储的顺序二叉树，也有利用链表进行存储的链式二叉树，在这个基础上又展开了二叉树的遍历。

二叉树的遍历分为前序遍历，中序遍历以及后序遍历，主要区别在于遍历的顺序不同。

前序遍历：

（1）访问根结点。

（2）前序遍历左子树。

（3）前序遍历右子树 。

中序遍历：

（1）中序遍历左子树

（2）访问根结点

（3）中序遍历右子树

后序遍历：

1）后序遍历左子树

（2）后序遍历右子树

（3）访问根结点

---

对于二叉树树的遍历的应用：

 

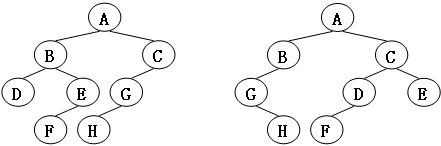
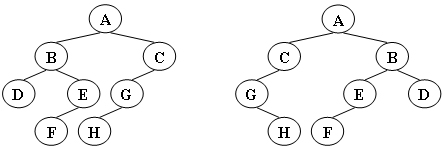
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2，则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的，因为我们把其中一棵树的结点A、B、G的左右孩子互换后，就得到另外一棵树。而图2就不是同构的。

 

 

图1

图2

现给定两棵树，请你判断它们是否是同构的。

 

输入格式:

输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。

输出格式:

如果两棵树是同构的，输出“Yes”，否则输出“No”。

输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

---

对于这道题我的想法是用双亲表示法来存储每一个结点，然后分别比较两颗树的每一个结点数据所对应的双亲是否相同，从而判断两棵树是否同构。

#include <iostream>
using namespace std;

typedef struct TreeNode //定义一个树的结构 
{
	char data; //结点的数据 
	char parent; //结点的双亲 
}TreeNode;

bool input_output() //boll类型函数判断二叉树是否同构 
{
	int i,j; //定义参数 
	
	TreeNode tree1[10],tree2[10]; //定义两个数的结构 
	
	char ltree,rtree; //定义两个字符参数 
	
	int n; //定义结点数参数 
	cin>>n; //输入第一棵树的结点数 
	
	for(i=0;i<n;i++)
	{
		tree1[i].parent=‘0‘; //将第一棵树的所有结点的parent赋值为‘0‘ 
	}
	
	for(i=0;i<n;i++)
	{
		cin>>tree1[i].data; //输入结点数据 
		cin>>ltree>>rtree; //输入结点对应的左右子结点 
		
		if(ltree!=‘-‘) //若子结点不为空 
		{
			j=ltree-48; //字符类型转换为int型，得到结点对应下标 
			tree1[j].parent = tree1[i].data ; //将结点的data值赋给子结点的parent 
		}
		
		if(rtree!=‘-‘) //若子结点不为空 
		{
			j=rtree-48; //字符类型转换为int型，得到结点对应下标 
			tree1[j].parent = tree1[i].data; //将结点的data值赋给子结点的parent
		}	
	}
	
	int m; //定义结点数参数
	cin>>m; //输入第二棵树的结点数
	
	for(i=0;i<m;i++)
	{
		tree2[i].parent=‘0‘; //将第二棵树的所有结点的parent赋值为‘0‘ 
	}
	
	for(i=0;i<m;i++)
	{
		cin>>tree2[i].data; //输入结点数据 
		cin>>ltree>>rtree; //输入结点对应的左右子结点 
		
		if(ltree!=‘-‘) //若子结点不为空 
		{
			j=ltree-48; //字符类型转换为int型，得到结点对应下标 
			tree2[j].parent = tree2[i].data; //将结点的data值赋给子结点的parent
		}
		
		if(rtree!=‘-‘) //若子结点不为空 
		{
			j=rtree-48; //字符类型转换为int型，得到结点对应下标 
			tree2[j].parent = tree2[i].data; //将结点的data值赋给子结点的parent
		}	
	}
	
	if(m!=n)return false; //若结点数不同，返回flase 
	
	if(m==1&&n==1&&tree1[0].data==tree2[0].data)return true; //结点数都为1，直接比较数据值，若为真则返回true 
	else if(m==1&&n==1&&tree1[0].data!=tree2[0].data)return false; //若为假则返回false 
	
	for(i=0;i<n;i++)
	{
		for(j=0;j<m;j++)
		{
			if(tree1[i].data==tree2[j].data) //若两棵树的某一结点数据值相同，则比较其双亲 
			{
				if(tree1[i].parent!=tree2[j].parent) //若双亲不同，则返回false 
				{
					return false;
				}
			}
		}
	}
	
	return true; //双亲相同，返回true 
}

int main()
{
	bool a = input_output(); //定义bool型参数 
	
	if(a)cout<<"Yes"; //两棵树同构，输出“Yes” 
	else cout<<"No"; //两棵树不同构，输出“No” 
	
	return 0;
}