CodeCraft-19 and Codeforces Round #537 (Div. 2) - D. Destroy the Colony(动态规划+组合数学)
Posted npugen
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了CodeCraft-19 and Codeforces Round #537 (Div. 2) - D. Destroy the Colony(动态规划+组合数学)相关的知识,希望对你有一定的参考价值。
Problem CodeCraft-19 and Codeforces Round #537 (Div. 2) - D. Destroy the Colony
Time Limit: 2000 mSec
![技术图片]() Problem Description
Problem Description

Input
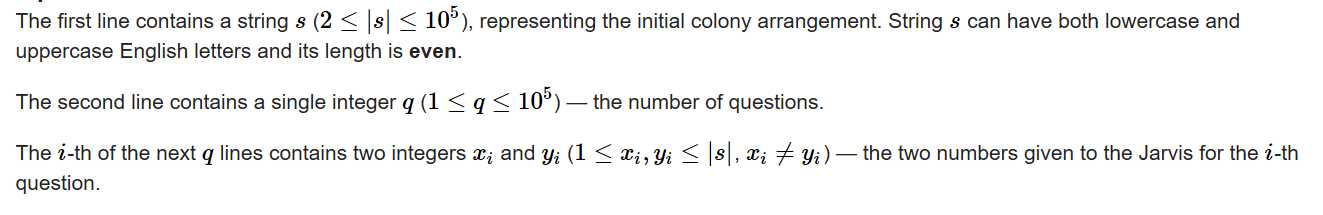
![技术图片]() Output
Output
For each question output the number of arrangements possible modulo 10^9+7.
![技术图片]() Sample Input
Sample Input
abba
2
1 4
1 2
![技术图片]() Sample Output
Sample Output
2
0
题解:这个题的每一部分都比较简单,加在一起就有难度了。关于组合数学的部分就不说了,比较简单,这个题的精华在于dp的部分,对于每次的询问,相当于强制让两种字符不在左边(或者不在右边),也就是在原始的dp递推方程中要跳过这两个字符的方案数,如果每次都重新递推,递推的复杂度是O(n * k),一共有k^2个组合,复杂度会炸,这时就要考虑利用之前dp的信息来减少递推的计算量,新的tmp_dp[j]的状态定义长度为j的,没有第i种字符的方案数,这其实就是长度为j的总方案数减去强制有第i种字符的方案数,而强制有i的方案数就应该是没有i的长度为j - cnt[i]的方案数,这恰好就是tmp_dp[j - cnt[i]],因此tmp[j] = dp[j] - tmp_dp[j - cnt[i]],可以在O(n)的时间内完成递推,一共有k^2个组合,因此复杂度时O(n * k^2),可以接受。
1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define REP(i, n) for (int i = 1; i <= (n); i++) 6 #define sqr(x) ((x) * (x)) 7 8 const int maxn = 100000 + 10; 9 const int maxm = 200000 + 100; 10 const int maxs = 52; 11 12 typedef long long LL; 13 typedef pair<int, int> pii; 14 typedef pair<double, double> pdd; 15 16 const LL unit = 1LL; 17 const int INF = 0x3f3f3f3f; 18 const LL Inf = 0x3f3f3f3f3f3f3f3f; 19 const double eps = 1e-14; 20 const double inf = 1e15; 21 const double pi = acos(-1.0); 22 const LL mod = 1000000007; 23 24 inline int cal(char ch) 25 { 26 if (isupper(ch)) 27 return ch - ‘A‘ + 26; 28 return ch - ‘a‘; 29 } 30 31 LL pow_mod(LL x, LL n, LL mod) 32 { 33 LL ans = 1, base = x; 34 while (n) 35 { 36 if (n & 1) 37 ans = (ans * base) % mod; 38 base = (base * base) % mod; 39 n >>= 1; 40 } 41 return ans; 42 } 43 44 void Add(LL &a, LL b) 45 { 46 a += b; 47 if (a > mod) 48 a -= mod; 49 } 50 51 void Sub(LL &a, LL b) 52 { 53 a -= b; 54 if (a < 0) 55 a += mod; 56 } 57 58 string str; 59 LL n; 60 LL cnt[maxs]; 61 LL fact[maxn], inv[maxn]; 62 LL dp[maxn], tmp_dp[maxn]; 63 LL ans[maxs][maxs]; 64 65 int main() 66 { 67 ios::sync_with_stdio(false); 68 cin.tie(0); 69 //freopen("input.txt", "r", stdin); 70 //freopen("output.txt", "w", stdout); 71 cin >> str; 72 n = str.size(); 73 for (int i = 0; i < n; i++) 74 { 75 cnt[cal(str[i])]++; 76 } 77 fact[0] = fact[1] = 1; 78 for (LL i = 2; i <= n; i++) 79 { 80 fact[i] = (fact[i - 1] * i) % mod; 81 } 82 inv[n] = pow_mod(fact[n], mod - 2, mod); 83 for (LL i = n - 1; i >= 0; i--) 84 { 85 inv[i] = (inv[i + 1] * (i + 1)) % mod; 86 } 87 LL num = (fact[n / 2] * fact[n / 2]) % mod; 88 for (int i = 0; i < maxs; i++) 89 { 90 num = (num * inv[cnt[i]]) % mod; 91 } 92 dp[0] = 1; 93 for (int i = 0; i < maxs; i++) 94 { 95 if (!cnt[i]) 96 continue; 97 for (int j = n; j >= cnt[i]; j--) 98 { 99 Add(dp[j], dp[j - cnt[i]]); 100 } 101 } 102 for (int i = 0; i < maxs; i++) 103 { 104 ans[i][i] = dp[n / 2]; 105 } 106 for (int i = 0; i < maxs; i++) 107 { 108 if (!cnt[i]) 109 continue; 110 for (int i = 0; i <= n; i++) 111 tmp_dp[i] = dp[i]; 112 for (int t = cnt[i]; t <= n; t++) 113 { 114 Sub(tmp_dp[t], tmp_dp[t - cnt[i]]); 115 } 116 for (int j = i + 1; j < maxs; j++) 117 { 118 if (!cnt[j]) 119 continue; 120 for (int t = cnt[j]; t <= n; t++) 121 { 122 Sub(tmp_dp[t], tmp_dp[t - cnt[j]]); 123 ans[i][j] = (2LL * tmp_dp[n / 2]) % mod; 124 ans[j][i] = ans[i][j]; 125 } 126 for (int t = n; t >= cnt[j]; t--) 127 Add(tmp_dp[t], tmp_dp[t - cnt[j]]); 128 } 129 } 130 int q; 131 cin >> q; 132 int x, y; 133 while (q--) 134 { 135 cin >> x >> y; 136 int l = cal(str[x - 1]); 137 int r = cal(str[y - 1]); 138 cout << (num * ans[l][r]) % mod << "\\n"; 139 } 140 return 0; 141 }
以上是关于CodeCraft-19 and Codeforces Round #537 (Div. 2) - D. Destroy the Colony(动态规划+组合数学)的主要内容,如果未能解决你的问题,请参考以下文章