二叉树

Posted 2021-11-26 zhangsonglin

一、 树的基本概念

为什么需要树呢？我们知道有序数组在进行插入和删除数据的时候效率太低，而链表的查找效率也很低，为了综合的解决有序数组和链表的缺点，树就产生了，在树中，能够非常快速的进行查找数据项、插入数据项、删除数据项。
在树中的几个概念：
· 路径：顺着连接节点的边从一个节点到另外一个节点，所经过的节点顺序排列称为路径；
· 根：树最上面的节点称为根节点，一棵树只有一个根节点，而且从根节点到任何节点有且只有一条路径；
· 父节点：每个节点都有一条边向上连接到上一个节点，那么这个节点的上一个节点就是父节点；
· 子节点：每一个节点都有一条边连接到下一个节点，下面的节点就是该节点的子节点；
· 叶子节点：没有子节点的节点称为叶子节点；
· 子树：每一个节点都可以作为一个子树的根，它和它的所有的子节点，子节点的子节点组合在一起，就是一颗子树；
· 访问：访问一个节点是为了在这个节点上进行一些操作，比如访问节点的数据项；
· 层：一个节点的层数是指从根节点到这个节点的代数

二、 二叉树（重点）
二叉树：树的每个几点最多只有两个子节点，称为二叉树。
范例：将一组数列：10,23,34,12,56,64,23,34 ,7,9,5

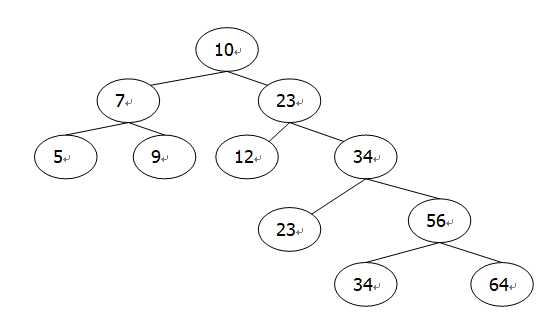
二叉树节点类：

public class Node {
    private int data;//节点数据项
    private Node leftChild;
    private Node rightChild;
    public int getData() {
        return data;
    }
    public void setData(int data) {
        this.data = data;
    }
    public Node getLeftChild() {
        return leftChild;
    }
    public void setLeftChild(Node leftChild) {
        this.leftChild = leftChild;
    }
    public Node getRightChild() {
        return rightChild;
    }
    public void setRightChild(Node rightChild) {
        this.rightChild = rightChild;
    }
    public Node(int data) {
        this.data = data;
    }
}

三、 二叉树节点插入
从根节点开始查找一个相应的节点，这个节点将称为即将插入节点的父节点，当这个父节点找到后，通过判断新插入节点的数据项比父节点的数据项的大小来决定是作为父节点的左子节点还是右子节点。
10,7,5,9,23,12,34

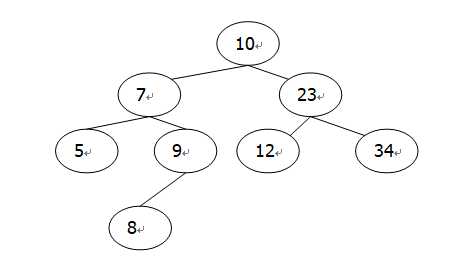
将数据项为8的节点插入上面的二叉树中。
代码实现：
/**
* 插入节点
* @param value
*/

    public void insert(int value) {
        //将数据封装成节点
        Node newNode = new Node(value);
        //引用当前节点
        Node current = root;
        //引用父节点
        Node parent = null;
        //如果根节点就是空的情况下，要插入的节点就是根节点
        if(root == null) {
            root = newNode;
        }else {
            while(true) {
                //父节点指向当前节点
                parent = current;
                //如果当前节点的数据比插入的数据要大，则向左走
                if(current.getData() > value) {
                    current = current.getLeftChild();
                    if(current == null) {//表示如果左子节点没有的话，则要插入的节点就是左子节点
                        parent.setLeftChild(newNode);
                        return;
                    }
                }else {//向右
                    current  = current.getRightChild();
                    if(current == null) {
                        parent.setRightChild(newNode);
                        return;
                    }
                }
            }
        }

测试类：

public class TreeTest {
    public static void main(String[] args) {
        Tree tree = new Tree();
        tree.insert(10);
        tree.insert(7);
        tree.insert(5);
        tree.insert(9);
        tree.insert(23);
        tree.insert(12);
        tree.insert(34);
        tree.insert(8);
        System.out.println(tree.getRoot().getData());
        System.out.println(tree.getRoot().getLeftChild().getRightChild().getLeftChild().getData());
    }
    
}

四、二叉树节点查找
设定从根节点为当前节点，如果查找的节点比当前节点要大，则继续查找当前节点的右子节点，如果查找的节点比当前节点要小，则继续查找当前节点的左子节点。

/**
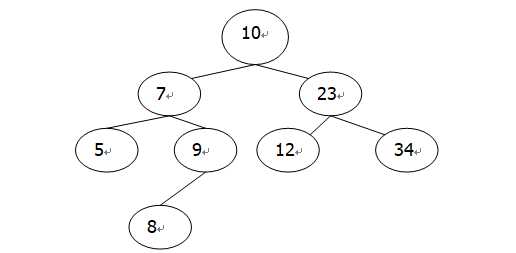
* 查找节点
* @param value
* 返回查找到的节点
*/

    public Node find(int value) {
        Node current = root;//引用当前节点为根节点
        //循环，只要查找到的数据项的值部位查找数据的话，继续循环
        while(current.getData() != value) {
            if(current.getData() > value) {//查找数据比当前节点的数据项要小
                current = current.getLeftChild();
            }else {
                current = current.getRightChild();
            }
            if(current == null) {//循环到了最后一个节点
                return null;
            }
        }
        
        return current;
    }
    ```
测试类：
public class TreeTest {
    public static void main(String[] args) {
        Tree tree = new Tree();
        tree.insert(10);
        tree.insert(7);
        tree.insert(5);
        tree.insert(9);
        tree.insert(23);
        tree.insert(12);
        tree.insert(34);
        tree.insert(8);
//      System.out.println(tree.getRoot().getData());
//      System.out.println(tree.getRoot().getLeftChild().getRightChild().getLeftChild().getData());
        
        Node node = tree.find(34);
        System.out.println(node.getData());
    }
    
}

上面的操作，数据项是一个单纯的int数据，现在比如每个节点除了保存int数据外，还保存了一个String数据。
五、二叉树遍历
遍历二叉树是根据一个特定的顺序去访问树的每一个节点，根据顺序不同，分为前序遍历、中序遍历和后序遍历。
· 前序遍历：
访问根节点
访问左子树
访问右子树
范例：10,7,5,9,8,23,12,34
· 中序遍历
遍历左子树
遍历根节点
遍历右子树
范例：5,7,8,9,10,12,23,34
· 后序遍历
遍历左子树
遍历右子树
遍历根节点
范例：5,8,9,7,12,34,23,10

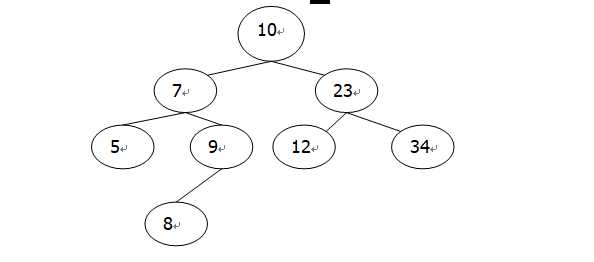
其实可以发现，三种遍历和递归都很有关系：
· 前序遍历
/**
* 前序遍历
* @param localNode
*/

    public void frontOrder(Node localNode) {
        if(null != localNode) {
            //访问根节点
            System.out.println(localNode.getData() + "====>" + localNode.getSdata());
            frontOrder(localNode.getLeftChild());//访问左子树
            frontOrder(localNode.getRightChild());//访问右子树
        }
    }

测试前序遍历：

tree.frontOrder(tree.getRoot());

· 中序遍历
/**
* 中序遍历
* @param localNode
*/

    public void inOrder(Node localNode) {
        if(null != localNode) {
            inOrder(localNode.getLeftChild());
            System.out.println(localNode.getData() + "====>" + localNode.getSdata());
            inOrder(localNode.getRightChild());
        }
    }

测试：

tree.inOrder(tree.getRoot());

· 后序遍历
/**
* 后序遍历
* @param localNode
*/

    public void afterOrder(Node localNode) {
        if(null != localNode) {
            afterOrder(localNode.getLeftChild());
            afterOrder(localNode.getRightChild());
            System.out.println(localNode.getData() + "====>" + localNode.getSdata());
        }
    }

测试：

tree.afterOrder(tree.getRoot());