[Algorithm] Inorder Successor in a binary search tree

Posted 2021-11-25 answer1215

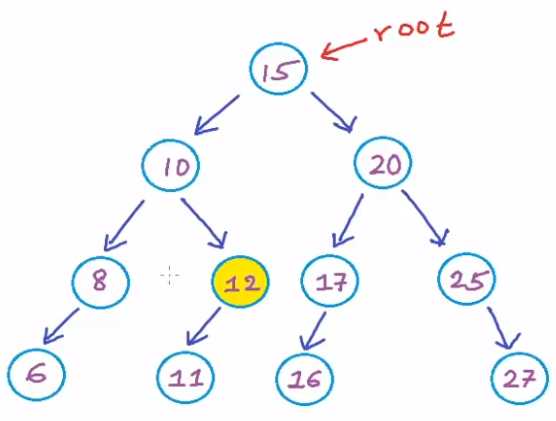
For the given tree, in order traverse is:

• visit left side
• root
• visit right side

// 6,8,10,11,12,15,16,17,20,25,27

 

The successor is the one right next to the target:

// target 8 --> succossor is 10

 

So, given the tree and target node, to find its successor.

Require knowledge how recurise call work, mainly it should reach the leaf node, then print it from bottom to top. For the node which has both right and left side, it visits left first, then itself, then right side. 

function findCurrent(root, val) {
  let current = root;
  let found = null;
  while (current !== null) {
    if (current.val === val) {
      found = current;
      break;
    } else if (current.val < val) {
      current = current.right;
    } else {
      current = current.left;
    }
  }

  return found;
}

function findMin(root) {
  // min should be on the left side
  while (root.left != null) {
    root = root.left;
  }

  return root;
}

function findSuccsor(root, val) {
  const current = findCurrent(root, val);
  if (current == null) {
    return null;
  }
  // case 1: Node has right subtree
  // Find min on the right part of the node
  // the min should be on the left most
  if (current.right != null) {
    return findMin(current.right);
  }
  // case 2: Node has no right subtree
  // --> A. target node can be on the left side like 8
  // --> B. target node can be on the right side like 12
  else {
    let parent = root;
    let found = null;
    while (parent !== current) {
      // A: if target is smaller than parent, means on the left side
      // then we keep going down to find target, its parent should be
      // the successor
      if (current.val < parent.val) {
        found = parent;
        parent = parent.left;
      } 
      // B: it target is larger than parent, means on the right side
      // then it means the parent node should already been visited
      // so we should not set successor in this case
      else {
        parent = parent.right;
      }
    }

    return found;
  }
}

function Node(val) {
  return {
    val,
    left: null,
    right: null
  };
}

function Tree() {
  return {
    root: null,
    addLeft(val, root) {
      const node = Node(val);
      root.left = node;
      return root.left;
    },
    addRight(val, root) {
      const node = Node(val);
      root.right = node;
      return root.right;
    }
  };
}

const tree = new Tree();
const root = Node(15);
tree.root = root;
const n1 = tree.addLeft(10, tree.root);
const n2 = tree.addRight(20, tree.root);

const n3 = tree.addLeft(8, n1);
tree.addLeft(6, n3);

const n4 = tree.addRight(12, n1);
tree.addLeft(11, n4);

const n5 = tree.addLeft(17, n2);
const n6 = tree.addLeft(16, n5);
const n7 = tree.addRight(25, n2);
tree.addRight(27, n7);
// inorder
// 6,8,10,11,12,15,16,17,20,25,27
// successor is the one next to the target
// target 8 --> succossor is 10
console.log(findSuccsor(tree.root, 27));