遗传算法求解TSP源码及解析

Posted 2021-11-25 qiankun-tec

遗传算法求解TSP源码及解析

1.算法效果

 

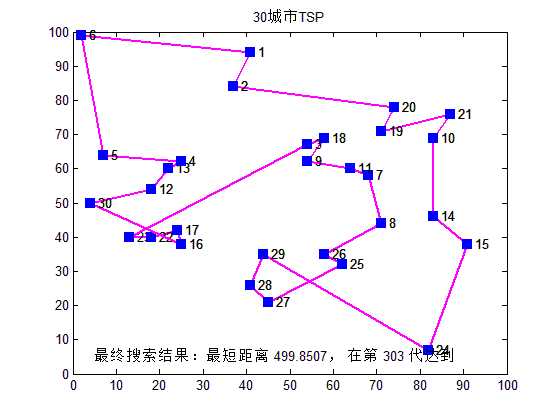
图 1?1算法效果1

 

 

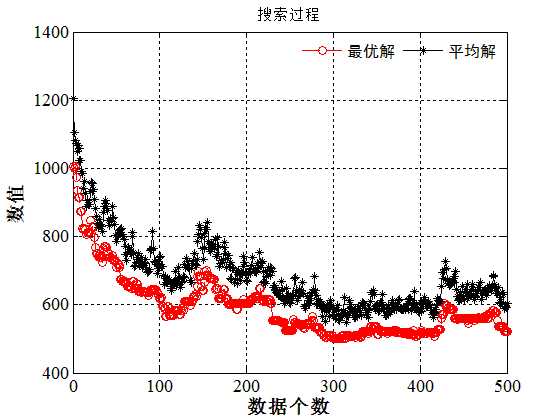
图 1?2算法效果2

2.原理说明

TSP问题是指假设有一个旅行商人要拜访n个城市，他必须选择所要走的路径，路径的限制是每个城市只能拜访一次，而且最后要回到原来出发的城市。路径的选择目标是要求得的路径路程为所有路径之中的最小值。本文使用遗传算法解决att30问题，即30个城市的旅行商问题。

旅行商问题是一个经典的组合优化问题。一个经典的旅行商问题可以描述为：一个商品推销员要去若干个城市推销商品，该推销员从一个城市出发，需要经过所有城市后，回到出发地。应如何选择行进路线，以使总的行程最短。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的Hamilton回路。由于该问题的可行解是所有顶点的全排列，随着顶点数的增加，会产生组合爆炸，它是一个NP完全问题。

TSP问题可以分为对称和不对称。在对称TSP问题中，两座城市之间来回的距离是相等的，形成一个无向图，而不对称TSP则形成有向图。对称性TSP问题可以将解的数量减少了一半。所以本次实验的TSP问题使用att48数据，可在tsplib中下载数据包。

演化算法是一类模拟自然界遗传进化规律的仿生学算法，它不是一个具体的算法，而是一个算法簇。遗传算法是演化算法的一个分支，由于遗传算法的整体搜索策略和优化计算是不依赖梯度信息，所以它的应用比较广泛。我们本次实验同样用到了遗传算法（用MATLAB编写）来解决TSP问题。

 

图 2?1算法流程图

3.源码说明

3.1.主函数

function ga_TSP

global data1 flag1

flag1=1;

close all

CityNum=30; %you chan choose 10, 30, 50, 75

[dislist,Clist]=tsp(CityNum);

%%  需要修改部分参数

inn=30; %初始种群大小

gnmax=100;  %最大代数

% gnmax=20;  %最大代数

pc=0.8; %交叉概率

pm=0.8; %变异概率

%%

%产生初始种群

s=zeros(inn,CityNum);

for i=1:inn

    s(i,:)=randperm(CityNum);

end

[~,p]=objf(s,dislist);

 

gn=1;

ymean=zeros(gn,1);

ymax=zeros(gn,1);

xmax=zeros(inn,CityNum);

scnew=zeros(inn,CityNum);

smnew=zeros(inn,CityNum);

while gn<gnmax+1

    for j=1:2:inn

        seln=sel(p);  %选择操作

        scro=cro(s,seln,pc);  %交叉操作

        scnew(j,:)=scro(1,:);

        scnew(j+1,:)=scro(2,:);

        smnew(j,:)=mut(scnew(j,:),pm);  %变异操作

        smnew(j+1,:)=mut(scnew(j+1,:),pm);

    end

    s=smnew;  %产生了新的种群

    [f,p]=objf(s,dislist);  %计算新种群的适应度

    %记录当前代最好和平均的适应度

    [fmax,nmax]=max(f);

    ymean(gn)=1000/mean(f);

    ymax(gn)=1000/fmax;

    %记录当前代的最佳个体

    x=s(nmax,:);

    xmax(gn,:)=x;

    drawTSP(Clist,x,ymax(gn),gn,0);

    gn=gn+1;

end

[min_ymax,index]=min(ymax);

drawTSP(Clist,xmax(index,:),min_ymax,index,1);

%%

% keyboard

% h2=figure(2);

% plot(ymax,‘r‘); hold on;

% plot(ymean,‘b‘);grid;

% title(‘搜索过程‘);

% legend(‘最优解‘,‘平均解‘);

% fprintf(‘遗传算法得到的最短距离:%.2f\\n‘,min_ymax);

% fprintf(‘遗传算法得到的最短路线‘);

% disp(xmax(index,:));

%%  绘图

% keyboard

h2=figure(2);

plot(ymax,‘ro--‘);

hold on;

plot(ymean,‘k*--‘);grid;

title(‘搜索过程‘);

fprintf(‘遗传算法得到的最短距离:%.2f\\n‘,min_ymax);

fprintf(‘遗传算法得到的最短路线‘);

disp(xmax(index,:));

% set(gca,‘unit‘,‘centimeters‘,‘position‘,[2.5 1.2 25 5.5])

% set(gcf,‘unit‘,‘centimeters‘,‘position‘,[3 3 28 7])%%整个图的信息

set(gca,‘FontName‘,‘Times New Roman‘,‘FontSize‘,14)%设置坐标轴字体大小，字型

set(gcf,‘WindowStyle‘,‘normal‘);

grid  on

box on

h1=legend(‘最优解‘,‘平均解‘);

set(h1,‘box‘,‘off‘, ‘Orientation‘,‘horizontal‘,‘FontSize‘,12,‘FontName‘,‘黑体‘);

xlabel(‘\\bf数据个数‘);ylabel(‘\\bf数值‘);

grid on

% keyboard

end

 

%------------------------------------------------

%计算所有种群的适应度

function [f,p]=objf(s,dislist)

 

inn=size(s,1);  %读取种群大小

f=zeros(inn,1);

for i=1:inn

    f(i)=CalDist(dislist,s(i,:));  %计算函数值，即适应度

end

f=1000./f‘; %取距离倒数

 

%根据个体的适应度计算其被选择的概率

fsum=0;

for i=1:inn

    fsum=fsum+f(i)^15;% 让适应度越好的个体被选择概率越高

end

ps=zeros(inn,1);

for i=1:inn

    ps(i)=f(i)^15/fsum;

end

 

%计算累积概率

p=zeros(inn,1);

p(1)=ps(1);

for i=2:inn

    p(i)=p(i-1)+ps(i);

end

p=p‘;

end

 

%--------------------------------------------------

%根据变异概率判断是否变异

function pcc=pro(pc)

test(1:100)=0;

l=round(100*pc);

test(1:l)=1;

n=round(rand*99)+1;

pcc=test(n);

end

 

%--------------------------------------------------

%“选择”操作

function seln=sel(p)

 

seln=zeros(2,1);

%从种群中选择两个个体，最好不要两次选择同一个个体

for i=1:2

    r=rand;  %产生一个随机数

    prand=p-r;

    j=1;

    while prand(j)<0

        j=j+1;

    end

    seln(i)=j; %选中个体的序号

    if i==2&&j==seln(i-1)    %%若相同就再选一次

        r=rand;  %产生一个随机数

        prand=p-r;

        j=1;

        while prand(j)<0

            j=j+1;

        end

    end

end

end

 

%------------------------------------------------

%“交叉”操作

function scro=cro(s,seln,pc)

 

bn=size(s,2);

pcc=pro(pc);  %根据交叉概率决定是否进行交叉操作，1则是，0则否

scro(1,:)=s(seln(1),:);

scro(2,:)=s(seln(2),:);

if pcc==1

    c1=round(rand*(bn-2))+1;  %在[1,bn-1]范围内随机产生一个交叉位

    c2=round(rand*(bn-2))+1;

    chb1=min(c1,c2);

    chb2=max(c1,c2);

    middle=scro(1,chb1+1:chb2);

    scro(1,chb1+1:chb2)=scro(2,chb1+1:chb2);

    scro(2,chb1+1:chb2)=middle;

    for i=1:chb1 %似乎有问题

        while find(scro(1,chb1+1:chb2)==scro(1,i))

            zhi=find(scro(1,chb1+1:chb2)==scro(1,i));

            y=scro(2,chb1+zhi);

            scro(1,i)=y;

        end

        while find(scro(2,chb1+1:chb2)==scro(2,i))

            zhi=find(scro(2,chb1+1:chb2)==scro(2,i));

            y=scro(1,chb1+zhi);

            scro(2,i)=y;

        end

    end

    for i=chb2+1:bn

        while find(scro(1,1:chb2)==scro(1,i))

            zhi=logical(scro(1,1:chb2)==scro(1,i));

            y=scro(2,zhi);

            scro(1,i)=y;

        end

        while find(scro(2,1:chb2)==scro(2,i))

            zhi=logical(scro(2,1:chb2)==scro(2,i));

            y=scro(1,zhi);

            scro(2,i)=y;

        end

    end

end

end

 

%--------------------------------------------------

%“变异”操作

function snnew=mut(snew,pm)

 

bn=size(snew,2);

snnew=snew;

 

pmm=pro(pm);  %根据变异概率决定是否进行变异操作，1则是，0则否

if pmm==1

    c1=round(rand*(bn-2))+1;  %在[1,bn-1]范围内随机产生一个变异位

    c2=round(rand*(bn-2))+1;

    chb1=min(c1,c2);

    chb2=max(c1,c2);

    x=snew(chb1+1:chb2);

    snnew(chb1+1:chb2)=fliplr(x);

end

end

 

%------------------------------------------------

%城市位置坐标

function [DLn,cityn]=tsp(n)

DLn=zeros(n,n);

if n==10

    city10=[0.4 0.4439;0.2439 0.1463;0.1707 0.2293;0.2293 0.761;0.5171 0.9414;

        0.8732 0.6536;0.6878 0.5219;0.8488 0.3609;0.6683 0.2536;0.6195 0.2634];%10 cities d‘=2.691

    for i=1:10

        for j=1:10

            DLn(i,j)=((city10(i,1)-city10(j,1))^2+(city10(i,2)-city10(j,2))^2)^0.5;

        end

    end

    cityn=city10;

end

if n==30

    city30=[41 94;37 84;54 67;25 62;7 64;2 99;68 58;71 44;54 62;83 69;64 60;18 54;22 60;

        83 46;91 38;25 38;24 42;58 69;71 71;74 78;87 76;18 40;13 40;82 7;62 32;58 35;45 21;41 26;44 35;4 50];%30 cities d‘=423.741 by D B Fogel

    for i=1:30

        for j=1:30

            DLn(i,j)=((city30(i,1)-city30(j,1))^2+(city30(i,2)-city30(j,2))^2)^0.5;

        end

    end

    cityn=city30;

end

 

if n==50

    city50=[31 32;32 39;40 30;37 69;27 68;37 52;38 46;31 62;30 48;21 47;25 55;16 57;

        17 63;42 41;17 33;25 32;5 64;8 52;12 42;7 38;5 25; 10 77;45 35;42 57;32 22;

        27 23;56 37;52 41;49 49;58 48;57 58;39 10;46 10;59 15;51 21;48 28;52 33;

        58 27;61 33;62 63;20 26;5 6;13 13;21 10;30 15;36 16;62 42;63 69;52 64;43 67];%50 cities d‘=427.855 by D B Fogel

    for i=1:50

        for j=1:50

            DLn(i,j)=((city50(i,1)-city50(j,1))^2+(city50(i,2)-city50(j,2))^2)^0.5;

        end

    end

    cityn=city50;

end

 

if n==75

    city75=[48 21;52 26;55 50;50 50;41 46;51 42;55 45;38 33;33 34;45 35;40 37;50 30;

        55 34;54 38;26 13;15 5;21 48;29 39;33 44;15 19;16 19;12 17;50 40;22 53;21 36;

        20 30;26 29;40 20;36 26;62 48;67 41;62 35;65 27;62 24;55 20;35 51;30 50;

        45 42;21 45;36 6;6 25;11 28;26 59;30 60;22 22;27 24;30 20;35 16;54 10;50 15;

        44 13;35 60;40 60;40 66;31 76;47 66;50 70;57 72;55 65;2 38;7 43;9 56;15 56;

        10 70;17 64;55 57;62 57;70 64;64 4;59 5;50 4;60 15;66 14;66 8;43 26];%75 cities d‘=549.18 by D B Fogel

    for i=1:75

        for j=1:75

            DLn(i,j)=((city75(i,1)-city75(j,1))^2+(city75(i,2)-city75(j,2))^2)^0.5;

        end

    end

    cityn=city75;

end

% if n==30

%     city30=[41 94;37 84;54 67;25 62;7 64;2 99;68 58;71 44;54 62;83 69;64 60;18 54;22 60;

%         83 46;91 38;25 38;24 42;58 69;71 71;74 78;87 76;18 40;13 40;82 7;62 32;58 35;45 21;41 26;44 35;4 50];%30 cities d‘=423.741 by D B Fogel

%     for i=1:30

%         for j=1:30

%             DLn(i,j)=((city30(i,1)-city30(j,1))^2+(city30(i,2)-city30(j,2))^2)^0.5;

%         end

%     end

%     cityn=city30;

% end

 

end

%%

 

%------------------------------------------------

%适应度函数

function F=CalDist(dislist,s)

 

DistanV=0;

n=size(s,2);

for i=1:(n-1)

    DistanV=DistanV+dislist(s(i),s(i+1));

end

DistanV=DistanV+dislist(s(n),s(1));

F=DistanV;

 

end

 

%------------------------------------------------

%画图

function drawTSP(Clist,BSF,bsf,p,f)

global data1 flag1

CityNum=size(Clist,1);

for i=1:CityNum-1

    plot([Clist(BSF(i),1),Clist(BSF(i+1),1)],[Clist(BSF(i),2),Clist(BSF(i+1),2)],‘ms-‘,‘LineWidth‘,2,‘MarkerEdgeColor‘,‘b‘,‘MarkerFaceColor‘,‘b‘);

    text(Clist(BSF(i),1),Clist(BSF(i),2),[‘  ‘,int2str(BSF(i))]);

    text(Clist(BSF(i+1),1),Clist(BSF(i+1),2),[‘  ‘,int2str(BSF(i+1))]);

    hold on;

end

plot([Clist(BSF(CityNum),1),Clist(BSF(1),1)],[Clist(BSF(CityNum),2),Clist(BSF(1),2)],‘ms-‘,‘LineWidth‘,2,‘MarkerEdgeColor‘,‘b‘,‘MarkerFaceColor‘,‘b‘);

title([num2str(CityNum),‘城市TSP‘]);

if f==0&&CityNum~=10

    text(5,5,[‘第 ‘,int2str(p),‘ 代‘,‘  最短距离为 ‘,num2str(bsf)]);

else

    text(5,5,[‘最终搜索结果：最短距离 ‘,num2str(bsf),‘， 在第 ‘,num2str(p),‘ 代达到‘]);

end

data1(flag1)=bsf;

flag1=flag1+1;

sum(Clist);

if CityNum==10

    if f==0

        text(0,0,[‘第 ‘,int2str(p),‘ 代‘,‘  最短距离为 ‘,num2str(bsf)]);

    else

        text(0,0,[‘最终搜索结果：最短距离 ‘,num2str(bsf),‘， 在第 ‘,num2str(p),‘ 代达到‘]);

    end

end

hold off;

pause(0.02);

% keyboard

end

3.2.子函数1

function qiankun_tec

global data1 flag1 mm data

flag1=1;

% mainly amended by Chen Zhen, 2012~2016

close all

% CityNum=30; %you chan choose 10, 30, 50, 75

% [dislist,Clist]=tsp(CityNum);

load data

[mm nn]=size(data);

CityNum=mm;

[dislist,Clist]=tsp(CityNum);

 

inn=30; %初始种群大小

gnmax=500;  %最大代数

% gnmax=20;  %最大代数

pc=0.8; %交叉概率

pm=0.8; %变异概率

 

%产生初始种群

s=zeros(inn,CityNum);

for i=1:inn

    s(i,:)=randperm(CityNum);

end

[~,p]=objf(s,dislist);

 

gn=1;

ymean=zeros(gn,1);

ymax=zeros(gn,1);

xmax=zeros(inn,CityNum);

scnew=zeros(inn,CityNum);

smnew=zeros(inn,CityNum);

while gn<gnmax+1

    for j=1:2:inn

        seln=sel(p);  %选择操作

        scro=cro(s,seln,pc);  %交叉操作

        scnew(j,:)=scro(1,:);

        scnew(j+1,:)=scro(2,:);

        smnew(j,:)=mut(scnew(j,:),pm);  %变异操作

        smnew(j+1,:)=mut(scnew(j+1,:),pm);

    end

    s=smnew;  %产生了新的种群

    [f,p]=objf(s,dislist);  %计算新种群的适应度

    %记录当前代最好和平均的适应度

    [fmax,nmax]=max(f);

    ymean(gn)=1000/mean(f);

    ymax(gn)=1000/fmax;

    %记录当前代的最佳个体

    x=s(nmax,:);

    xmax(gn,:)=x;

    drawTSP(Clist,x,ymax(gn),gn,0);

    gn=gn+1;

end

[min_ymax,index]=min(ymax);

drawTSP(Clist,xmax(index,:),min_ymax,index,1);

%%

% keyboard

% h2=figure(2);

% plot(ymax,‘r‘); hold on;

% plot(ymean,‘b‘);grid;

% title(‘搜索过程‘);

% legend(‘最优解‘,‘平均解‘);

% fprintf(‘遗传算法得到的最短距离:%.2f\\n‘,min_ymax);

% fprintf(‘遗传算法得到的最短路线‘);

% disp(xmax(index,:));

%%  绘图

% keyboard

h2=figure(2);

plot(ymax,‘ro--‘);

hold on;

plot(ymean,‘k*--‘);grid;

title(‘搜索过程‘);

fprintf(‘遗传算法得到的最短距离:%.2f\\n‘,min_ymax);

fprintf(‘遗传算法得到的最短路线‘);

disp(xmax(index,:));

% set(gca,‘unit‘,‘centimeters‘,‘position‘,[2.5 1.2 25 5.5])

% set(gcf,‘unit‘,‘centimeters‘,‘position‘,[3 3 28 7])%%整个图的信息

set(gca,‘FontName‘,‘Times New Roman‘,‘FontSize‘,14)%设置坐标轴字体大小，字型

set(gcf,‘WindowStyle‘,‘normal‘);

grid  on

box on

h1=legend(‘最优解‘,‘平均解‘);

set(h1,‘box‘,‘off‘, ‘Orientation‘,‘horizontal‘,‘FontSize‘,12,‘FontName‘,‘黑体‘);

xlabel(‘\\bf数据个数‘);ylabel(‘\\bf数值‘);

grid on

% keyboard

end

 

%------------------------------------------------

%计算所有种群的适应度

function [f,p]=objf(s,dislist)

 

inn=size(s,1);  %读取种群大小

f=zeros(inn,1);

for i=1:inn

    f(i)=CalDist(dislist,s(i,:));  %计算函数值，即适应度

end

f=1000./f‘; %取距离倒数

 

%根据个体的适应度计算其被选择的概率

fsum=0;

for i=1:inn

    fsum=fsum+f(i)^15;% 让适应度越好的个体被选择概率越高

end

ps=zeros(inn,1);

for i=1:inn

    ps(i)=f(i)^15/fsum;

end

 

%计算累积概率

p=zeros(inn,1);

p(1)=ps(1);

for i=2:inn

    p(i)=p(i-1)+ps(i);

end

p=p‘;

end

 

%--------------------------------------------------

%根据变异概率判断是否变异

function pcc=pro(pc)

test(1:100)=0;

l=round(100*pc);

test(1:l)=1;

n=round(rand*99)+1;

pcc=test(n);

end

 

%--------------------------------------------------

%“选择”操作

function seln=sel(p)

 

seln=zeros(2,1);

%从种群中选择两个个体，最好不要两次选择同一个个体

for i=1:2

    r=rand;  %产生一个随机数

    prand=p-r;

    j=1;

    while prand(j)<0

        j=j+1;

    end

    seln(i)=j; %选中个体的序号

    if i==2&&j==seln(i-1)    %%若相同就再选一次

        r=rand;  %产生一个随机数

        prand=p-r;

        j=1;

        while prand(j)<0

            j=j+1;

        end

    end

end

end

 

%------------------------------------------------

%“交叉”操作

function scro=cro(s,seln,pc)

 

bn=size(s,2);

pcc=pro(pc);  %根据交叉概率决定是否进行交叉操作，1则是，0则否

scro(1,:)=s(seln(1),:);

scro(2,:)=s(seln(2),:);

if pcc==1

    c1=round(rand*(bn-2))+1;  %在[1,bn-1]范围内随机产生一个交叉位

    c2=round(rand*(bn-2))+1;

    chb1=min(c1,c2);

    chb2=max(c1,c2);

    middle=scro(1,chb1+1:chb2);

    scro(1,chb1+1:chb2)=scro(2,chb1+1:chb2);

    scro(2,chb1+1:chb2)=middle;

    for i=1:chb1 %似乎有问题

        while find(scro(1,chb1+1:chb2)==scro(1,i))

            zhi=find(scro(1,chb1+1:chb2)==scro(1,i));

            y=scro(2,chb1+zhi);

            scro(1,i)=y;

        end

        while find(scro(2,chb1+1:chb2)==scro(2,i))

            zhi=find(scro(2,chb1+1:chb2)==scro(2,i));

            y=scro(1,chb1+zhi);

            scro(2,i)=y;

        end

    end

    for i=chb2+1:bn

        while find(scro(1,1:chb2)==scro(1,i))

            zhi=logical(scro(1,1:chb2)==scro(1,i));

            y=scro(2,zhi);

            scro(1,i)=y;

        end

        while find(scro(2,1:chb2)==scro(2,i))

            zhi=logical(scro(2,1:chb2)==scro(2,i));

            y=scro(1,zhi);

            scro(2,i)=y;

        end

    end

end

end

 

%--------------------------------------------------

%“变异”操作

function snnew=mut(snew,pm)

 

bn=size(snew,2);

snnew=snew;

 

pmm=pro(pm);  %根据变异概率决定是否进行变异操作，1则是，0则否

if pmm==1

    c1=round(rand*(bn-2))+1;  %在[1,bn-1]范围内随机产生一个变异位

    c2=round(rand*(bn-2))+1;

    chb1=min(c1,c2);

    chb2=max(c1,c2);

    x=snew(chb1+1:chb2);

    snnew(chb1+1:chb2)=fliplr(x);

end

end

 

%------------------------------------------------

%城市位置坐标

function [DLn,cityn]=tsp(n)

DLn=zeros(n,n);

if n==10

    city10=[0.4 0.4439;0.2439 0.1463;0.1707 0.2293;0.2293 0.761;0.5171 0.9414;

        0.8732 0.6536;0.6878 0.5219;0.8488 0.3609;0.6683 0.2536;0.6195 0.2634];%10 cities d‘=2.691

    for i=1:10

        for j=1:10

            DLn(i,j)=((city10(i,1)-city10(j,1))^2+(city10(i,2)-city10(j,2))^2)^0.5;

        end

    end

    cityn=city10;

end

if n==30

    city30=[41 94;37 84;54 67;25 62;7 64;2 99;68 58;71 44;54 62;83 69;64 60;18 54;22 60;

        83 46;91 38;25 38;24 42;58 69;71 71;74 78;87 76;18 40;13 40;82 7;62 32;58 35;45 21;41 26;44 35;4 50];%30 cities d‘=423.741 by D B Fogel

    for i=1:30

        for j=1:30

            DLn(i,j)=((city30(i,1)-city30(j,1))^2+(city30(i,2)-city30(j,2))^2)^0.5;

        end

    end

    cityn=city30;

end

 

if n==50

    city50=[31 32;32 39;40 30;37 69;27 68;37 52;38 46;31 62;30 48;21 47;25 55;16 57;

        17 63;42 41;17 33;25 32;5 64;8 52;12 42;7 38;5 25; 10 77;45 35;42 57;32 22;

        27 23;56 37;52 41;49 49;58 48;57 58;39 10;46 10;59 15;51 21;48 28;52 33;

        58 27;61 33;62 63;20 26;5 6;13 13;21 10;30 15;36 16;62 42;63 69;52 64;43 67];%50 cities d‘=427.855 by D B Fogel

    for i=1:50

        for j=1:50

            DLn(i,j)=((city50(i,1)-city50(j,1))^2+(city50(i,2)-city50(j,2))^2)^0.5;

        end

    end

    cityn=city50;

end

 

if n==75

    city75=[48 21;52 26;55 50;50 50;41 46;51 42;55 45;38 33;33 34;45 35;40 37;50 30;

        55 34;54 38;26 13;15 5;21 48;29 39;33 44;15 19;16 19;12 17;50 40;22 53;21 36;

        20 30;26 29;40 20;36 26;62 48;67 41;62 35;65 27;62 24;55 20;35 51;30 50;

        45 42;21 45;36 6;6 25;11 28;26 59;30 60;22 22;27 24;30 20;35 16;54 10;50 15;

        44 13;35 60;40 60;40 66;31 76;47 66;50 70;57 72;55 65;2 38;7 43;9 56;15 56;

        10 70;17 64;55 57;62 57;70 64;64 4;59 5;50 4;60 15;66 14;66 8;43 26];%75 cities d‘=549.18 by D B Fogel

    for i=1:75

        for j=1:75

            DLn(i,j)=((city75(i,1)-city75(j,1))^2+(city75(i,2)-city75(j,2))^2)^0.5;

        end

    end

    cityn=city75;

end

global mm data

if n==mm

    city30=data;

    for i=1:mm

        for j=1:mm

            DLn(i,j)=((city30(i,1)-city30(j,1))^2+(city30(i,2)-city30(j,2))^2)^0.5;

        end

    end

    cityn=city30;

end

 

end

%%

 

%------------------------------------------------

%适应度函数

function F=CalDist(dislist,s)

 

DistanV=0;

n=size(s,2);

for i=1:(n-1)

    DistanV=DistanV+dislist(s(i),s(i+1));

end

DistanV=DistanV+dislist(s(n),s(1));

F=DistanV;

 

end

 

%------------------------------------------------

%画图

function drawTSP(Clist,BSF,bsf,p,f)

global data1 flag1

CityNum=size(Clist,1);

for i=1:CityNum-1

    plot([Clist(BSF(i),1),Clist(BSF(i+1),1)],[Clist(BSF(i),2),Clist(BSF(i+1),2)],‘ms-‘,‘LineWidth‘,2,‘MarkerEdgeColor‘,‘b‘,‘MarkerFaceColor‘,‘b‘);

    text(Clist(BSF(i),1),Clist(BSF(i),2),[‘  ‘,int2str(BSF(i))]);

    text(Clist(BSF(i+1),1),Clist(BSF(i+1),2),[‘  ‘,int2str(BSF(i+1))]);

    hold on;

end

plot([Clist(BSF(CityNum),1),Clist(BSF(1),1)],[Clist(BSF(CityNum),2),Clist(BSF(1),2)],‘ms-‘,‘LineWidth‘,2,‘MarkerEdgeColor‘,‘b‘,‘MarkerFaceColor‘,‘b‘);

title([num2str(CityNum),‘城市TSP‘]);

if f==0&&CityNum~=10

    text(5,5,[‘第 ‘,int2str(p),‘ 代‘,‘  最短距离为 ‘,num2str(bsf)]);

else

    text(5,5,[‘最终搜索结果：最短距离 ‘,num2str(bsf),‘， 在第 ‘,num2str(p),‘ 代达到‘]);

end

data1(flag1)=bsf;

flag1=flag1+1;

sum(Clist);

if CityNum==10

    if f==0

        text(0,0,[‘第 ‘,int2str(p),‘ 代‘,‘  最短距离为 ‘,num2str(bsf)]);

    else

        text(0,0,[‘最终搜索结果：最短距离 ‘,num2str(bsf),‘， 在第 ‘,num2str(p),‘ 代达到‘]);

    end

end

hold off;

pause(0.02);

% keyboard

end

3.3.子函数2

function [ output_args ] = simulated ( input_args )

%UNTITLED Summary of this function goes here

%   Detailed explanation goes here

 

clc

a = 0.99;       % 温度衰减函数的参数

t0 = 99; tf = 0.1; t = t0;

ML = 500;     % Markov链长度

coordinates = [

    1   41 94;   2  37 84;  3   54  67;

    4    25 62;    5   7  64;  6    2     99;

    7    68 58;    8  71 44;   9     54   62;

    10  83 69;    11   64 60;    12   18   54;

    13  22 60;    14   83 46;    15   91   38;

    16  25 38;    17   24 42;    18   58   69;

    19  71 71;    20   74 78;    21   87   76;

    22  18 40;    23   13 40;    24   82   7;

    25  62 32;    26   58 35;    27   45   21;

    28  41 26;    29   44 35;    30   4     50;

    ];

coordinates(:,1) = [];

amount = size(coordinates,1);       % 城市的数目

% 通过向量化的方法计算距离矩阵

dist_matrix = zeros(amount, amount);

coor_x_tmp1 = coordinates(:,1) * ones(1,amount);

coor_x_tmp2 = coor_x_tmp1‘;

coor_y_tmp1 = coordinates(:,2) * ones(1,amount);

coor_y_tmp2 = coor_y_tmp1‘;

dist_matrix = sqrt((coor_x_tmp1-coor_x_tmp2).^2 + ...

    (coor_y_tmp1-coor_y_tmp2).^2);

 

sol_new = 1:amount;         % 产生初始解

% sol_new是每次产生的新解；sol_current是当前解；sol_best是冷却中的最好解；

E_current = inf;E_best = inf;          % E_current是当前解对应的回路距离；

% E_new是新解的回路距离；

% E_best是最优解的

sol_current = sol_new; sol_best = sol_new;

p = 1;                         %统计迭代次数

while t>=tf

    for r=1:ML          % Markov链长度

        if (rand < 0.5)    % 随机决定是进行两交换还是三交换

            % 两交换

            ind1 = 0; ind2 = 0;

            while (ind1 == ind2)

                ind1 = ceil(rand.*amount);

                ind2 = ceil(rand.*amount);

            end

            tmp1 = sol_new(ind1);

            sol_new(ind1) = sol_new(ind2);

            sol_new(ind2) = tmp1;

        else

            % 三交换

            ind1 = 0; ind2 = 0; ind3 = 0;

            while (ind1 == ind2) || (ind1 == ind3) ...

                    || (ind2 == ind3) || (abs(ind1-ind2) == 1)

                ind1 = ceil(rand.*amount);

                ind2 = ceil(rand.*amount);

                ind3 = ceil(rand.*amount);

            end

            tmp1 = ind1;tmp2 = ind2;tmp3 = ind3;

            % 确保ind1 < ind2 < ind3

            if (ind1 < ind2) && (ind2 < ind3)

                

            elseif (ind1 < ind3) && (ind3 < ind2)

                ind2 = tmp3;ind3 = tmp2;

            elseif (ind2 < ind1) && (ind1 < ind3)

                ind1 = tmp2;ind2 = tmp1;

            elseif (ind2 < ind3) && (ind3 < ind1)

                ind1 = tmp2;ind2 = tmp3; ind3 = tmp1;

            elseif (ind3 < ind1) && (ind1 < ind2)

                ind1 = tmp3;ind2 = tmp1; ind3 = tmp2;

            elseif (ind3 < ind2) && (ind2 < ind1)

                ind1 = tmp3;ind2 = tmp2; ind3 = tmp1;

            end

           

            tmplist1 = sol_new((ind1+1):(ind2-1));

            sol_new((ind1+1):(ind1+ind3-ind2+1)) = ...

                sol_new((ind2):(ind3));

            sol_new((ind1+ind3-ind2+2):ind3) = ...

                tmplist1;

            

        end

       

        %检查是否满足约束

       

        % 计算目标函数值

        E_new = 0;

        for i = 1 : (amount-1)

            E_new = E_new + ...

                dist_matrix(sol_new(i),sol_new(i+1));

        end

        % 再算上从最后一个城市到第一个城市的距离

        E_new = E_new + ...

            dist_matrix(sol_new(amount),sol_new(1));

       

        if E_new < E_current

            E_current = E_new;

            sol_current = sol_new;

            if E_new < E_best

                % 把冷却过程中最好的解保存下来

                E_best = E_new;

                sol_best = sol_new;

            end

        else

            % 若新解的目标函数值小于当前解的，

            % 则仅以一定概率接受新解

            if rand < exp(-(E_new-E_current)./t)

                E_current = E_new;

                sol_current = sol_new;

            else

                sol_new = sol_current;

            end

        end

    end

    t=t.*a;          % 控制参数t（温度）减少为原来的a倍

   

end

for i=1:length(coordinates)

    plot(coordinates(i,1),coordinates(i,2),‘r*‘);

    hold on;

end;

x=coordinates([sol_best sol_best(1)],1);

y=coordinates([sol_best sol_best(1)],2);

plot(x,y);

title([‘循环迭代次数:‘,int2str(ML),‘ 优化最短距离:‘,num2str(E_best)]);

end