已知点和线, 求垂足
Posted ouyxy
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了已知点和线, 求垂足相关的知识，希望对你有一定的参考价值。
- 已知点 \\(A(x_1, y_1)\\), 现有一条直线 \\(l\\): \\(ax+by+c=0\\), 直线 \\(l\\) 到\\(A\\) 的举例为 \\(d\\), 点 \\(A\\) 到直线 \\(l\\) 的垂足点记为 \\(B\\), 求 \\(B\\) 的坐标.
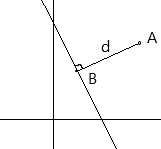
解答
已知直线的表达式, 可知直线上的一个垂线量为: \\((a,b)\\), 记 \\(B\\) 的坐标表示为 \\((x_2,y_2)\\), 那么向量 \\(\\overrightarrow{BA} = (x_1 - x_2, y_1 - y_2)\\), \\(d(A,B)=d\\), 所以, \\(\\frac{(a,b) \\cdot d}{\\left\\|(a,b)\\right\\|_2} = (x_1 - x_2, y_1 - y_2)\\), 所以 \\(B\\) 表示为:
\\[ (x_2,y_2)=(x_1,y_2) - \\frac{(a,b) \\cdot d}{\\left\\|(a,b)\\right\\|_2}, \\]
推向多项式表示, 超平面表示为 \\(\\omega x + b = 0\\), 点 \\(A\\) 坐标表示为 \\(x_0\\), \\(A\\) 到 \\(B\\) 的距离表示为 \\(\\gamma\\), 那么 \\(B\\) 表示为:
\\[ x_1 = x_0 - \\gamma \\cdot \\frac{\\omega}{\\left\\| \\omega \\right\\|_2} \\]
以上是关于已知点和线, 求垂足的主要内容，如果未能解决你的问题，请参考以下文章
Scala实现：已知三点坐标，求最短距离（如果在垂足不在线段内，最短距离为到其中一点的直线距离）
点和线之间的最短距离（Google Maps API 问题？）
Problem C: 平面上的点和线——Point类Line类 (III)
Problem G: 平面上的点和线——Point类Line类 (VII)