树-二叉查找树红黑树

Posted 2021-11-20 guixinchan

二叉查找树的性质：

• 如果节点的左子树不空，则左子树上所有结点的值均小于等于它的根结点的值；
• 如果节点的右子树不空，则右子树上所有结点的值均大于等于它的根结点的值；
• 任意节点的左、右子树也分别为二叉查找树；

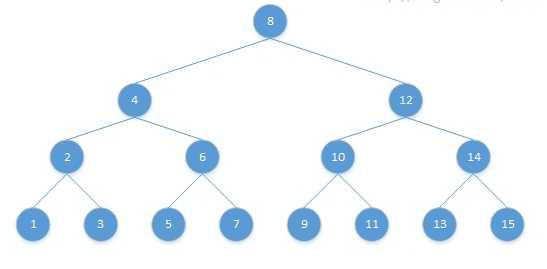
二叉查找树查找某个结点时，是二分查找的思想，查找所需的最大次数等同于二叉树的高度。

缺陷：二叉查找树多次插入新节点时，有可能导致二叉查找树的不平衡，变成线性结构。

二叉查找树的优化=> 红黑树

1.节点是红色或黑色。

2.根节点是黑色。

3.所有叶子都是黑色（叶子是NIL节点）。

4.每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）

5.从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。

操作：

因为每一个红黑树也是一个特化的二叉查找树，因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。然而，在红黑树上进行插入操作和删除操作会导致不再匹配红黑树的性质。恢复红黑树的性质需要少量 的颜色变更（实际是非常快速的）和不超过三次树旋转（对于插入操作是两次）。虽然插入和删除很复杂，但操作时间仍可以保持为次。

 红黑树调整的方法：变色和旋转（左旋转、右旋转）

 变色：为了满足红黑树的规则，尝试把红色节点变为黑色，或者把黑色节点变为红色。

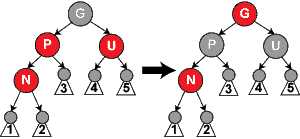
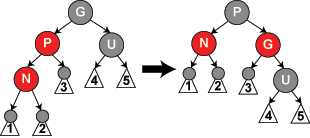
左旋转：逆时针旋转红黑树的两个节点，使得父节点被自己的右子节点取代，而父节点成为其左子节点。

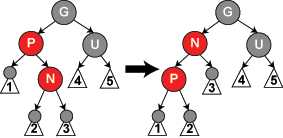
右旋转：顺时针旋转红黑树的两个节点，使得父节点被自己的左子节点取代，而父节点成为其右子节点。

红黑树的应用：TreeMap、TreeSet和java8中的HashMap

转自：基维百科