Python汉诺塔问题
Posted z2273533704
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python汉诺塔问题相关的知识,希望对你有一定的参考价值。
-
汉诺塔问题是一个经典的问题。汉诺塔(Hanoi Tower),又称河内塔,源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,任何时候,在小圆盘上都不能放大圆盘,且在三根柱子之间一次只能移动一个圆盘。问应该如何操作?
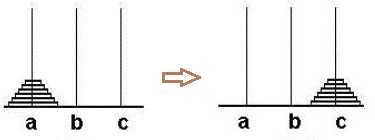
将其问题分解寻找规律
- 将b柱子作为辅助,把a上的63个圆盘移动到b上
- 将a上最后一个圆盘移动到c
- 将a作为辅助,把b上的62个圆盘移动到a上
- 将b上的最后一个圆盘移动到c
-
即每次都是先将其他圆盘移动到辅助柱子上,并将最底下的圆盘移到c柱子上,然后再把原先的柱子作为辅助柱子,并重复此过程。
著名的斐波那契数列定义如下,可以看出,f(n)是由规模更小一些的f(n-1)和f(n-2)推导出来的:
f(0)=0,f(1)=1
f(n)=f(n-1)+f(n-2) (n>=2)因此,递归实际上就是用自己来定义自己。
这个过程称为递归,即定义一组基本操作,这组操作将规模小一点(或大一点)的操作当做一个整体——无需关心它的细节,只当它已经完成了——然后执行剩下的操作。而在更小或更大的规模中也依此操作,直到规模达到预定值。
2.根据规律创建函数
我们假设函数func(n, a, b, c)用于将n个圆盘由a移动到c,b作为辅助柱子。那么我们可以这样实现这个递归过程:
-
func:
-
if n!=0 then ;预定值
-
func(n-1, a, c, b) ;将n-1个盘子由a移动到b,以c为辅助柱子(注意参数顺序)
-
move a[n] to c ;将a上的最后一个盘子移动到c
-
func(n-1, b, a, c) ;将n-1个盘子由b移动到c,以a为辅助柱子
-
endif ;完成
3.结合turtle构建函数
-
import turtle
-
-
class Stack:
-
-
def __init__(self):
-
-
self.items = []
-
-
def isEmpty(self):
-
-
return len(self.items) == 0
-
-
def push(self, item):
-
-
self.items.append(item)
-
-
def pop(self):
-
-
return self.items.pop()
-
-
def peek(self):
-
-
if not self.isEmpty():
-
-
return self.items[len(self.items) - 1]
-
-
def size(self):
-
-
return len(self.items)
-
-
-
-
def drawpole_3():
-
-
t = turtle.Turtle()
-
-
t.hideturtle()
-
-
def drawpole_1(k):
-
-
t.up()
-
-
t.pensize(10)
-
-
t.speed(100)
-
-
t.goto(400*(k-1), 400)
-
-
t.down()
-
-
t.goto(400*(k-1), -100)
-
-
t.goto(400*(k-1)-20, -100)
-
-
t.goto(400*(k-1)+20, -100)
-
-
drawpole_1(0)
-
-
drawpole_1(1)
-
-
drawpole_1(2)
-
-
-
-
def creat_plates(n):
-
-
plates=[turtle.Turtle() for i in range(n)]
-
-
for i in range(n):
-
-
plates[i].up()
-
-
plates[i].hideturtle()
-
-
plates[i].shape("square")
-
-
plates[i].shapesize(1,20-i)
-
-
plates[i].goto(-400,-90+20*i)
-
-
plates[i].showturtle()
-
-
return plates
-
-
-
-
def pole_stack():
-
-
poles=[Stack() for i in range(3)]
-
-
return poles
-
-
-
-
def moveDisk(plates,poles,fp,tp):
-
-
mov=poles[fp].peek()
-
-
plates[mov].goto((fp-1)*400,550)
-
-
plates[mov].goto((tp-1)*400,550)
-
-
l=poles[tp].size()
-
-
plates[mov].goto((tp-1)*400,-90+20*l)
-
-
-
-
def moveTower(plates,poles,height,fromPole, toPole, withPole):
-
-
if height >= 1:
-
-
moveTower(plates,poles,height-1,fromPole,withPole,toPole)
-
-
moveDisk(plates,poles,fromPole,toPole)
-
-
poles[toPole].push(poles[fromPole].pop())
-
-
moveTower(plates,poles,height-1,withPole,toPole,fromPole)
-
-
-
-
myscreen=turtle.Screen()
-
-
drawpole_3()
-
-
n=int(input("请输入汉诺塔的层数并回车:\\n"))
-
-
plates=creat_plates(n)
-
-
poles=pole_stack()
-
-
for i in range(n):
-
-
poles[0].push(i)
-
-
moveTower(plates,poles,n,0,2,1)
-
-
myscreen.exitonclick()
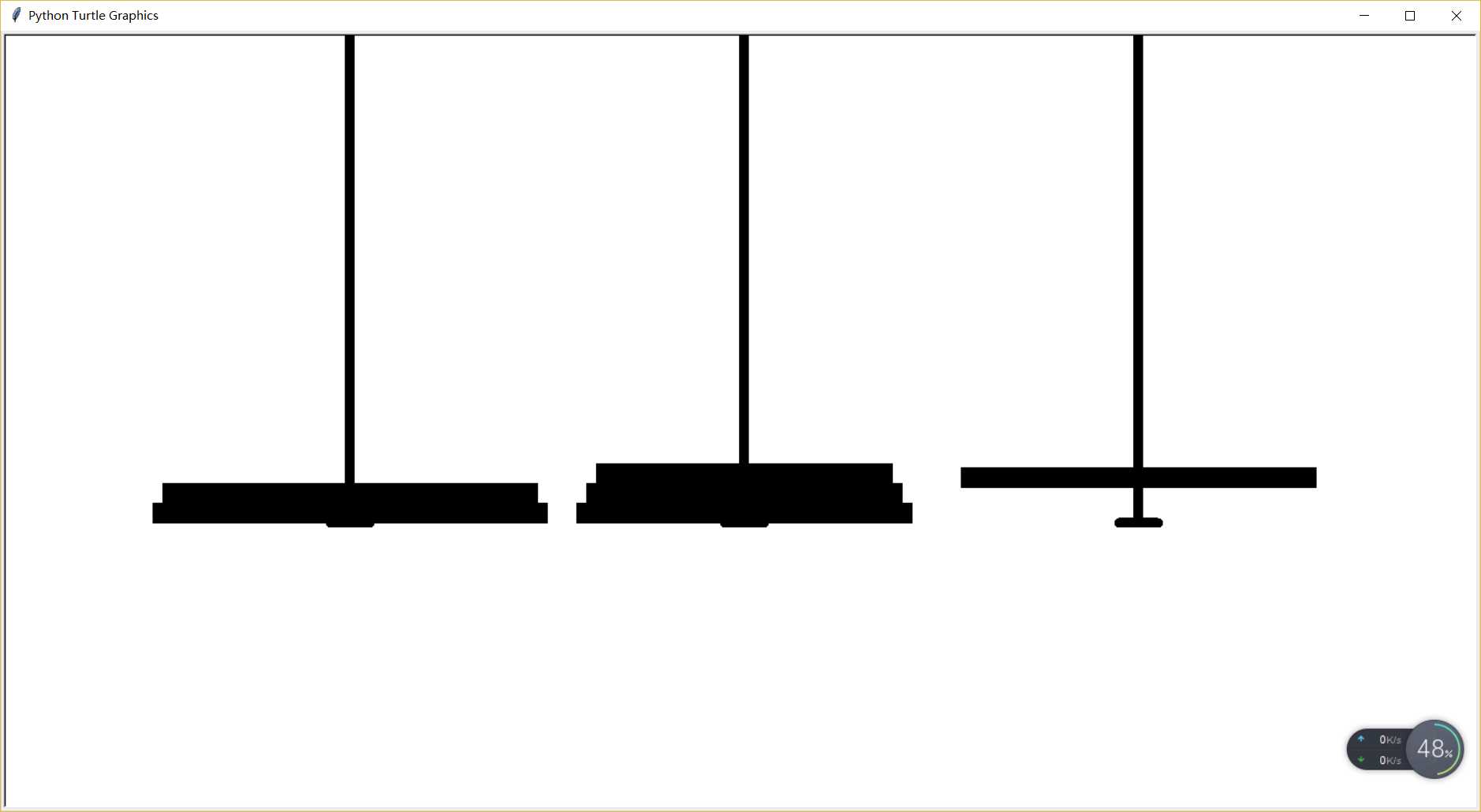
4.将该代码输入python并运行
运行过程如下图
-
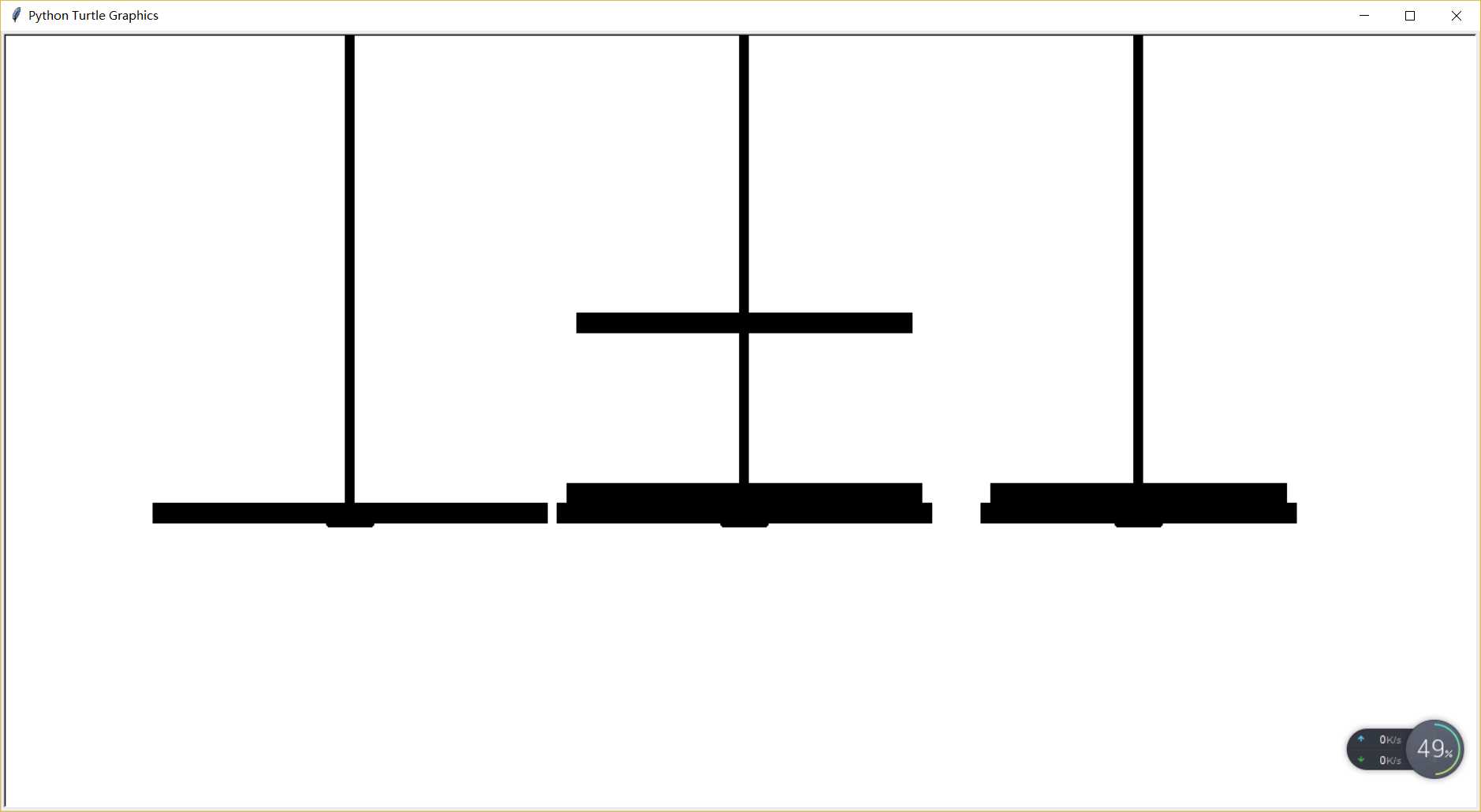
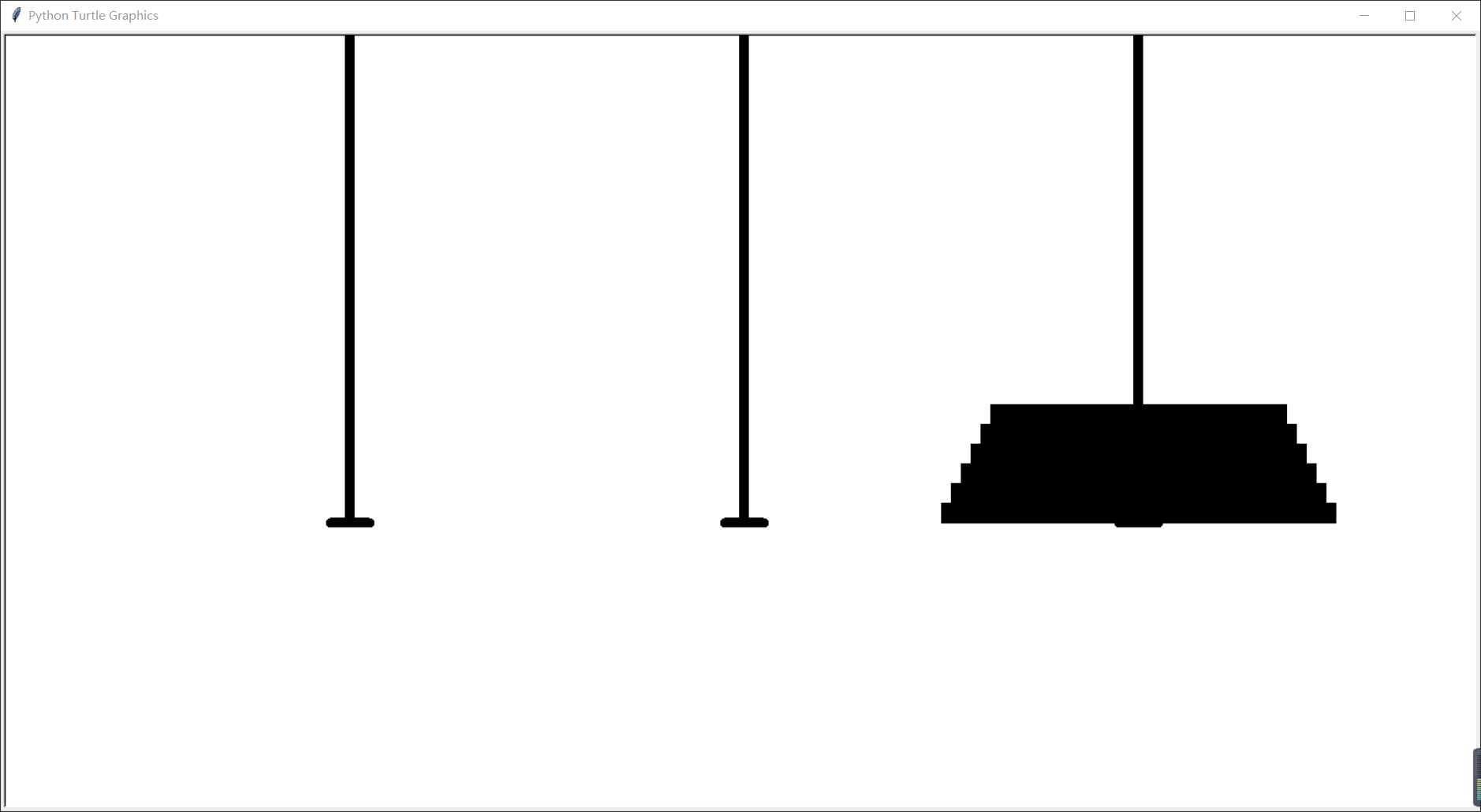
以上是关于Python汉诺塔问题的主要内容,如果未能解决你的问题,请参考以下文章