LQ-Nets: Learned Quantization for Highly Accurate and Compact Deep Neural Networks 论文阅读

Posted 2021-11-10 dushuxiang

• 摘要

　　虽然权重和激活量化是深度神经网络（DNN）压缩的有效方法，并且具有很多利用bit操作来提高推理速度的潜力，但在量化模型和完整模型之间的预测精度方面仍存在明显差距。为了解决这个差距，我们建议联合训练量化的，位操作兼容的DNN及其相关的量化器，而不是使用固定的手工量化方案，例如均匀或对数量化。我们学习量化器的方法适用于任意位精度的网络权重和激活，我们的量化器很容易训练。对CIFAR-10和ImageNet数据集的全面实验表明，我们的方法可以很好地适用于各种网络结构，如AlexNet，VGG-Net，GoogLeNet，ResNet和DenseNet，在准确度方面超过以前的量化方法。代码可从https://github.com/Microsoft/LQ-Nets获得

• 简介

　　我们建议联合训练量化的DNN及其相关的量化器。 所提出的方法不仅使量化器可学习，而且使它们与按位运算兼容，从而保持适当量化的神经网络的快速推理优点。 我们的量化器可以通过标准网络训练管道中的反向传播进行优化，并且我们进一步提出了一种基于量化误差最小化的算法，其产生更好的性能。 所提出的量化可以应用于网络权重和激活，并且可以实现任意比特宽度。 此外，可以应用具有非共享参数的分层量化器以获得进一步的灵活性。 我们将通过我们的方法量化的网络称为“LQ-Nets”。

　　我们使用CIFAR-10和ImageNet数据集上的图像分类任务评估我们的LQ-Nets。 实验结果表明，它们在各种网络结构中表现非常好，如AlexNet，VGG-Net，GoogLeNet，ResNet和DenseNet ，大大超过了以前的量化方法。

• LQ-Nets：具有学习量化的网络
• 网络量化

　　网络量化的目标是用几个bit表示浮点权重w和或激活a。 通常，量化函数是分段常数函数，可以写成

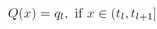
　　其中q_l，l = 1，...，L是量化等级，并且（t_l，t_{l + 1}）是量化间隔。量化函数将量化间隔内的所有输入值映射到相应的量化等级，并且量化值可以只用log₂L位编码。也许最简单的量化器是用于二进制量化的符号函数：如果x≥0则Q（x）= +1，否则为-1。对于2位或更多位的量化， 最常用的量化器是均匀量化函数，其中所有量化步长q_{1 + 1}-q_l相等。一些方法使用对数量化，其均匀地量化对数域中的数据。

　　量化网络权重可以生成高度紧凑且存储效率高的DNN模型：使用n位编码，与32位或64位浮点表示相比，压缩率为32/n或64/n。 此外，如果权重和激活都适当地量化，则W·a（w为参数，a为激活）的内积可以通过按位运算来计算，例如xnor和popcnt，其中xnor是异或非逻辑运算，popcnt计算位串中1的数量。 在大多数通用计算平台（如CPU和GPU）上，这两个操作都可以在一个或几个时钟周期内处理至少64位，这可能导致64倍的加速。

• 可学习的量化器

　　最佳量化器应该为输入数据分布产生最小的量化误差：

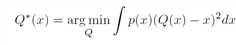
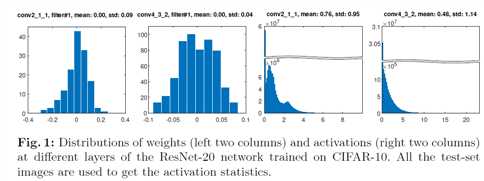
　　其中p（x）是x的概率密度函数。 我们永远无法确定诸如均匀量化器之类的流行量化器是否是网络权重和激活的最佳选择。 在图1中，我们在训练的浮点网络中呈现权重和激活（在批量归一化（BN）和整流线性单元（ReLU）层之后）的统计分布。 可以看出，分布可以是复杂的并且跨层不同，并且均匀量化器对于它们不是最佳的。 当然，如果我们训练量化网络，则权重和激活分布可能会改变。 但是我们再也无法确定任何预定义的量化器是否适合我们的任务，并且不正确的量化器很容易危及最终的准确性。

 

 　　为了获得更好的网络量化器并提高量化网络的准确性，我们建议联合训练网络及其量化器。 背后的见解是，如果优化器通过网络训练可以学习和优化，它们不仅可以最小化量化误差，还可以适应训练目标，从而提高最终的准确性。 训练量化器的简单方法是直接优化网络训练中的量化等级{q_l}。 然而，这种天真的策略会使量化函数与按位运算不兼容，这是不希望的，因为我们希望保持量化神经网络的快速推理优点。

 　　为了解决这个问题，我们需要将量化函数限制在与按位运算兼容的子空间中。 但是如何在训练期间将量化器限制在这样的空间中？ 我们的解决方案受到比特操作兼容的均匀量化的启发（参见[53]）。 均匀量化基本上将浮点数映射到具有归一化因子的最接近的定点整数，并且其与位不兼容的关键属性是量化值可以通过位的线性组合来分解。 具体地，由K位二进制编码表示的整数q实际上是基矢量和二进制编码矢量b = [b1，b2，...，bK] ^T之间的内积，其中bi∈{0,1}

 

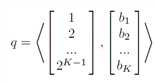
 　　为了学习量化器，同时保持它们与按位运算兼容，我们可以简单地学习由K标量组成的基矢量。

　　具体地说，我们可学习的量化函数形式为

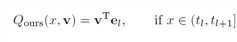
其中v∈R^K是可学习的浮点基，e_l∈{-1,1} ^K，图2说明了具有2位和3位情况的量化器。

• 训练算法

　　为了训练LQ-Nets，我们使用浮点网络权重，这些权重在卷积之前被量化并且通过误差反向传播（BP）和梯度下降进行优化。 训练之后，可以丢弃它们并保留它们的二进制码和量化基础。 我们现在介绍如何优化量化器。

　　量化器优化：优化量化器的一种简单而直接的方法是通过类似于权重优化的BP。 在这里，我们提出了一种基于量化误差最小化的算法，该算法在训练期间优化了前向通道中的量化器。 这个算法可以带来更好的性能，我们将在后面的实验中展示。