Burnside引理的感性证明

Posted 2021-11-07 maomao9173

\\(Burnside\\)引理的感性证明：

• 其中：\\(G\\)是置换集合，\\(|G|\\)是置换种数，\\(T_i\\)是第\\(i\\)类置换中的不动点数。

\\[L = \\frac{1}{|G|} * \\sum T_i\\]

我们以\\(2*2\\)的方格图染色来举例感性证明。

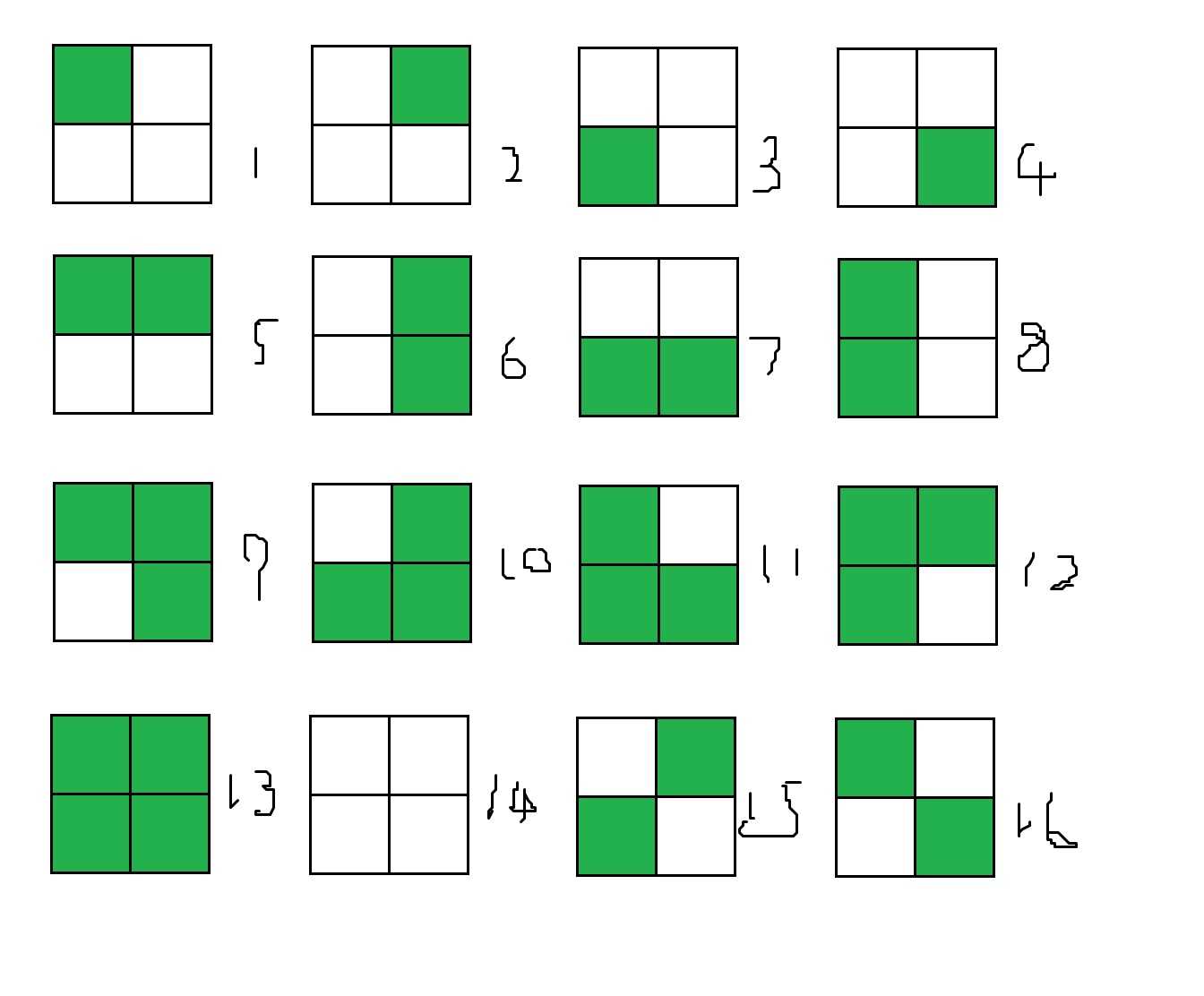
每个格子有\\(2\\)种方案，不考虑旋转重构一共就有\\(16\\)种。

其中对于每一种等价类（也可以称之为【旋转轨道】），他们上面的所有方案都是旋转重构的，我们只需要记一次就可以了。也就是说，我们所求的本质不同的方案数，其实就是等价类的个数。

• 置换\\(trans\\)的不动点：对于置换\\(trans\\)，置换后与自身相等不变的元素。

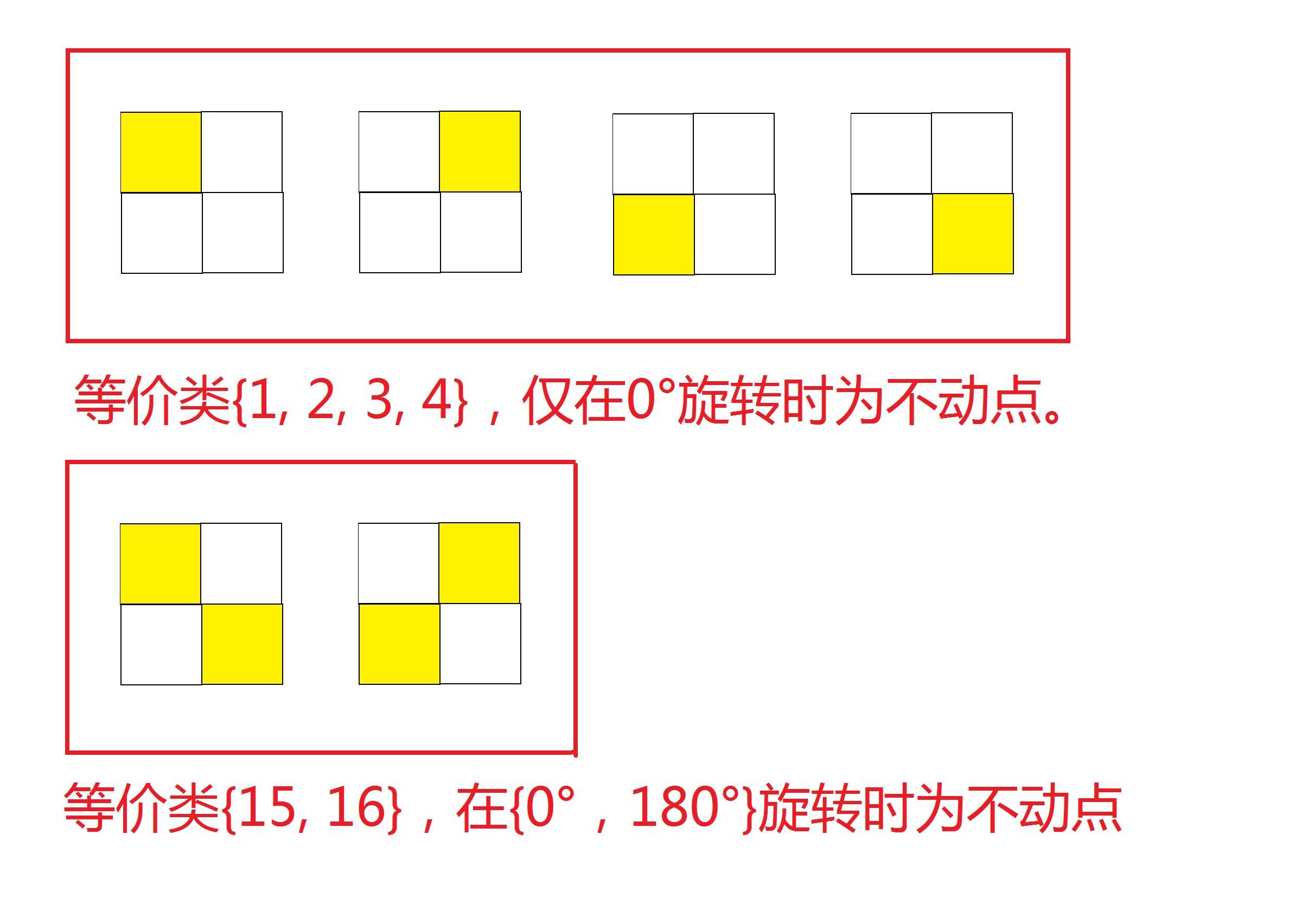
上面举出两种等价类的例子。可以看出，每一种等价类都在某些置换上是不动点（至少在0°是），且同一个等价类的所有元素，会同时作为\\(/\\)不作为某一个置换的不动点。手推一下可以得知，每一个等价类中所有元素，对不动点总数的贡献和恰好为\\(|G|\\)。

举例说明一下。

• \\(e.g\\)：
  • 元素\\(13\\)：在置换\\({1, 2, 3, 4}\\)中均为不动点
    • 和它同构的仅有它本身，该等价类对不动点贡献\\(=4\\)
  • 元素\\(15\\)：在置换\\(1, 3\\)中为不动点。
    • 和它同构的共有\\(|[1, 2]|=2\\)个元素，该等价类对不动点贡献\\(=4\\)
  • 元素\\(i\\)：在置换\\(1,k + 1, 2k + 1, ...pK+1\\)中为不动点
    • 和它同构的共有\\(|[1, k]|=k\\)个元素，该等价类对不动点贡献\\(=p*k=|G|\\) （\\(p =|G| / k\\)）

由此我们就证出来了这个公式。其实证了也没啥用，只是图一个用着安心。

\\[L = \\frac{1}{|G|} * \\sum T_i\\]