LCA算法
Posted morui
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了LCA算法相关的知识,希望对你有一定的参考价值。
概况
CA(Lowest Common Ancestors),即最近公共祖先,是指在有根树中,找出某两个结点u和v最近的公共祖先。
基本介绍
则有:
实现
暴力/Tarjan/DFS+ST/倍增
-
如果当前结点t 大于结点u、v,说明u、v都在t 的左侧,所以它们的共同祖先必定在t 的左子树中,故从t 的左子树中继续查找;
-
如果当前结点t 小于结点u、v,说明u、v都在t 的右侧,所以它们的共同祖先必定在t 的右子树中,故从t 的右子树中继续查找;
-
如果当前结点t 满足 u <t < v,说明u和v分居在t 的两侧,故当前结点t 即为最近公共祖先;
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
int query(Node t, Node u, Node v) { int left = u.value; int right = v.value; //二叉查找树内,如果左结点大于右结点,不对,交换 if (left > right) { int temp = left; left = right; right = temp; } while (true) { //如果t小于u、v,往t的右子树中查找 if (t.value < left) t = t.right; //如果t大于u、v,往t的左子树中查找 else if (t.value > right) t = t.left; else return t.value; }} |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
int tot, seq[N << 1], pos[N << 1], dep[N << 1];// dfs过程,预处理深度dep、dfs序数组seqvoid dfs(int now, int fa, int d) { pos[now] = ++tot, seq[tot] = now, dep[tot] = d; for (int i = head[now]; i; i = e[i].next) { int v = e[i].to; if (v == fa) continue; dfs(v, now, d + 1); seq[++tot] = now, dep[tot] = d; }}int anc[N << 1][20]; // anc[i][j]表示i节点向上跳2^j层对应的节点void init(int len) { for (int i = 1; i <= len; i++) anc[i][0] = i; for (int k = 1; (1 << k) <= len; k++) for (int i = 1; i + (1 << k) - 1 <= len; i++) if (dep[anc[i][k - 1]] < dep[anc[i + (1 << (k - 1))][k - 1]]) anc[i][k] = anc[i][k - 1]; else anc[i][k] = anc[i + (1 << (k - 1))][k - 1];}int rmq(int l, int r) { int k = log(r - l + 1) / log(2); return dep[anc[l][k]] < dep[anc[r + 1 - (1 << k)][k]] ? anc[l][k] : anc[r + 1 - (1 << k)][k];}int calc(int x, int y) { x = pos[x], y = pos[y]; if (x > y) swap(x, y); return seq[rmq(x, y)];}int lca(int a, int b) { dfs(root, 0, 1); // root为树根节点的编号 init(0); return calc(a, b);} |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
void dfs(int u) { for(int i=head[u]; i!=-1; i=edge[i].next) { int to=edge[i].to; if(to==p[u][0])continue; d[to]=d[u]+1; dist[to]=dist[u]+edge[i].w; p[to][0]=u; //p[i][0]存i的父节点 dfs(to); }}void init()//i的2^j祖先就是i的(2^(j-1))祖先的2^(j-1)祖先{ for(int j=1; (1<<j)<=n; j++) for(int i=1; i<=n; i++) p[i][j]=p[p[i][j-1]][j-1];}int lca(int a,int b) { if(d[a]>d[b])swap(a,b); //b在下面 int f=d[b]-d[a]; //f是高度差 for(int i=0; (1<<i)<=f; i++) //(1<<i)&f找到f化为2进制后1的位置,移动到相应的位置 if((1<<i)&f)b=p[b][i]; //比如f=5,二进制就是101,所以首先移动2^0祖先,然后再移动2^2祖先 if(a!=b) { for(int i=(int)log2(N); i>=0; i--) if(p[a][i]!=p[b][i]) //从最大祖先开始,判断a,b祖先,是否相同 a=p[a][i], b=p[b][i]; //如不相同,a b同时向上移动2^j a=p[a][0]; //这时a的father就是LCA } return a;} |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
|
const int mx = 10000; //最大顶点数int n, root; //实际顶点个数,树根节点int indeg[mx]; //顶点入度,用来判断树根vector<int> tree[mx]; //树的邻接表(不一定是二叉树)void inputTree() //输入树{ scanf("%d", &n); //树的顶点数 for (int i = 0; i < n; i++) //初始化树,顶点编号从0开始 tree[i].clear(), indeg[i] = 0; for (int i = 1; i < n; i++) //输入n-1条树边 { int x, y; scanf("%d%d", &x, &y); //x->y有一条边 tree[x].push_back(y); indeg[y]++;//加入邻接表,y入度加一 } for (int i = 0; i < n; i++) //寻找树根,入度为0的顶点 if (indeg[i] == 0) { root = i; break; }}vector<int> query[mx]; //所有查询的内容void inputQuires() //输入查询{ for (int i = 0; i < n; i++) //清空上次查询 query[i].clear(); int m; scanf("%d", &m); //查询个数 while (m--) { int u, v; scanf("%d%d", &u, &v); //查询u和v的LCA query[u].push_back(v); query[v].push_back(u); }}int father[mx], rnk[mx]; //节点的父亲、秩void makeSet() //初始化并查集{ for (int i = 0; i < n; i++) father[i] = i, rnk[i] = 0;}int findSet(int x) //查找{ if (x != father[x]) father[x] = findSet(father[x]); return father[x];}void unionSet(int x, int y) //合并{ x = findSet(x), y = findSet(y); if (x == y) return; if (rnk[x] > rnk[y]) father[y] = x; else father[x] = y, rnk[y] += rnk[x] == rnk[y];}int ancestor[mx]; //已访问节点集合的祖先bool vs[mx]; //访问标志void Tarjan(int x) //Tarjan算法求解LCA{ for (int i = 0; i < tree[x].size(); i++) { Tarjan(tree[x][i]); //访问子树 unionSet(x, tree[x][i]); //将子树节点与根节点x的集合合并 ancestor[findSet(x)] = x;//合并后的集合的祖先为x } vs[x] = 1; //标记为已访问 for (int i = 0; i < query[x].size(); i++) //与根节点x有关的查询 if (vs[query[x][i]]) //如果查询的另一个节点已访问,则输出结果 printf("%d和%d的最近公共祖先为:%d\\n", x, query[x][i], ancestor[findSet(query[x][i])]);}int main(){ inputTree(); //输入树 inputQuires();//输入查询 makeSet(); for (int i = 0; i < n; i++) ancestor[i] = i; memset(vs, 0, sizeof(vs)); //初始化为未访问 Tarjan(root);} |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
const int N=500004;int head[N*2],next[N*2],to[N*2];// 树的邻接表int deep[N],fa[N];// deep表示节点深度,fa表示节点的父亲int size[N],son[N],top[N];// size表示节点所在的子树的节点总数 // son表示节点的重孩子 // top表示节点所在的重链的顶部节点inline void add(int u,int v,int tnt)// 邻接表加边{ nt[tnt]=ft[u]; ft[u]=tnt; ed[tnt]=v;}void DFS(int u,int Fa)// 第一遍dfs,处理出deep,size,fa,son{ size[u]=1; for(int i=head[u];i;i=next[i]) { if(to[i]==Fa) continue; deep[to[i]]=d[u]+1; fa[to[i]]=u; DFS(to[i],u); size[u]+=size[to[i]]; if(size[to[i]]>size[son[u]]) son[u]=to[i]; }}void Dfs(int u)// 第二遍dfs,将所有相邻的重边连成重链{ if(u==son[fa[u]]) top[u]=top[fa[u]]; else top[u]=u; for(int i=head[u];i;i=next[i]) if(to[i]!=fa[u]) Dfs(to[i]);}int LCA(int u,int v)// 处理LCA{ while(top[u]!=top[v])// 如果u,v不在同一条重链上 { if(deep[top[u]]>deep[top[v]])// 将深度大的节点上调 u=fa[top[u]]; else v=fa[top[v]]; } return deep[u]>deep[v]?v:u;// 返回深度小的节点(即为LCA(u,v))} |
下面详细介绍一下Tarjan算法的基本思路:
1.任选一个点为根节点,从根节点开始。
2.遍历该点u所有子节点v,并标记这些子节点v已被访问过。
3.若是v还有子节点,返回2,否则下一步。
4.合并v到u上。
5.寻找与当前点u有询问关系的点v。
6.若是v已经被访问过了,则可以确认u和v的最近公共祖先为v被合并到的父亲节点a。
遍历的话需要用到dfs来遍历(我相信来看的人都懂吧...),至于合并,最优化的方式就是利用并查集来合并两个节点。
下面上伪代码:
1 Tarjan(u)//marge和find为并查集合并函数和查找函数
2 {
3 for each(u,v) //访问所有u子节点v
4 {
5 Tarjan(v); //继续往下遍历
6 marge(u,v); //合并v到u上
7 标记v被访问过;
8 }
9 for each(u,e) //访问所有和u有询问关系的e
10 {
11 如果e被访问过;
12 u,e的最近公共祖先为find(e);
13 }
14 }
个人感觉这样还是有很多人不太理解,所以我打算模拟一遍给大家看。
建议拿着纸和笔跟着我的描述一起模拟!!
假设我们有一组数据 9个节点 8条边 联通情况如下:
1--2,1--3,2--4,2--5,3--6,5--7,5--8,7--9 即下图所示的树
设我们要查找最近公共祖先的点为9--8,4--6,7--5,5--3;
设f[]数组为并查集的父亲节点数组,初始化f[i]=i,vis[]数组为是否访问过的数组,初始为0; 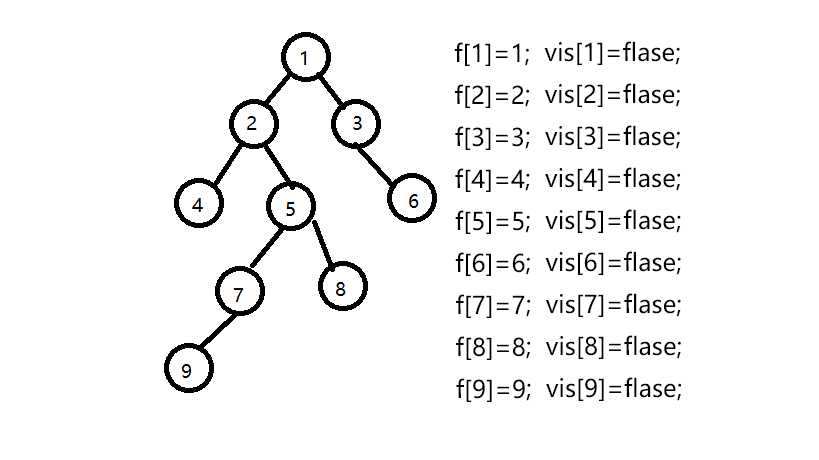
下面开始模拟过程:
取1为根节点,往下搜索发现有两个儿子2和3;
先搜2,发现2有两个儿子4和5,先搜索4,发现4没有子节点,则寻找与其有关系的点;
发现6与4有关系,但是vis[6]=0,即6还没被搜过,所以不操作;
发现没有和4有询问关系的点了,返回此前一次搜索,更新vis[4]=1;
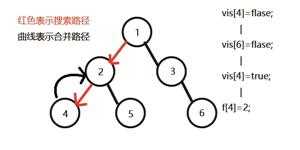
表示4已经被搜完,更新f[4]=2,继续搜5,发现5有两个儿子7和8;
先搜7,发现7有一个子节点9,搜索9,发现没有子节点,寻找与其有关系的点;
发现8和9有关系,但是vis[8]=0,即8没被搜到过,所以不操作;
发现没有和9有询问关系的点了,返回此前一次搜索,更新vis[9]=1;
表示9已经被搜完,更新f[9]=7,发现7没有没被搜过的子节点了,寻找与其有关系的点;
发现5和7有关系,但是vis[5]=0,所以不操作;
发现没有和7有关系的点了,返回此前一次搜索,更新vis[7]=1;
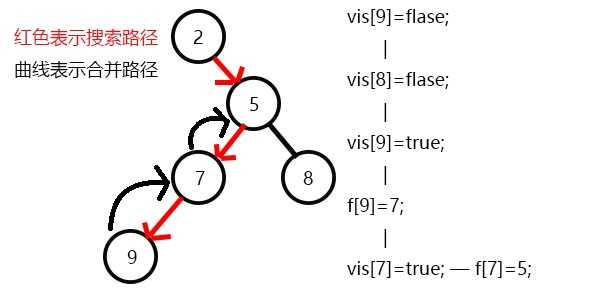
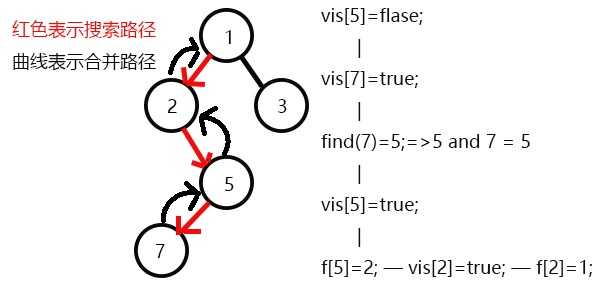
表示7已经被搜完,更新f[7]=5,继续搜8,发现8没有子节点,则寻找与其有关系的点;
发现9与8有关系,此时vis[9]=1,则他们的最近公共祖先为find(9)=5;
(find(9)的顺序为f[9]=7-->f[7]=5-->f[5]=5 return 5;)
发现没有与8有关系的点了,返回此前一次搜索,更新vis[8]=1;
表示8已经被搜完,更新f[8]=5,发现5没有没搜过的子节点了,寻找与其有关系的点;
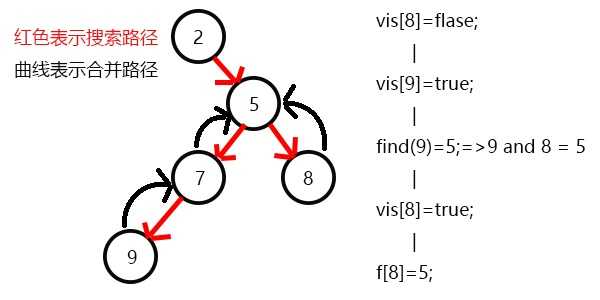
发现7和5有关系,此时vis[7]=1,所以他们的最近公共祖先为find(7)=5;
(find(7)的顺序为f[7]=5-->f[5]=5 return 5;)
又发现5和3有关系,但是vis[3]=0,所以不操作,此时5的子节点全部搜完了;
返回此前一次搜索,更新vis[5]=1,表示5已经被搜完,更新f[5]=2;
发现2没有未被搜完的子节点,寻找与其有关系的点;
又发现没有和2有关系的点,则此前一次搜索,更新vis[2]=1;
表示2已经被搜完,更新f[2]=1,继续搜3,发现3有一个子节点6;
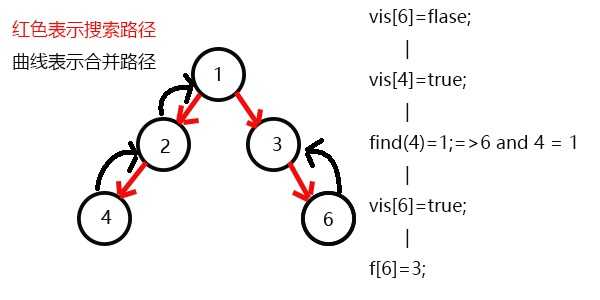
搜索6,发现6没有子节点,则寻找与6有关系的点,发现4和6有关系;
此时vis[4]=1,所以它们的最近公共祖先为find(4)=1;
(find(4)的顺序为f[4]=2-->f[2]=2-->f[1]=1 return 1;)
发现没有与6有关系的点了,返回此前一次搜索,更新vis[6]=1,表示6已经被搜完了;
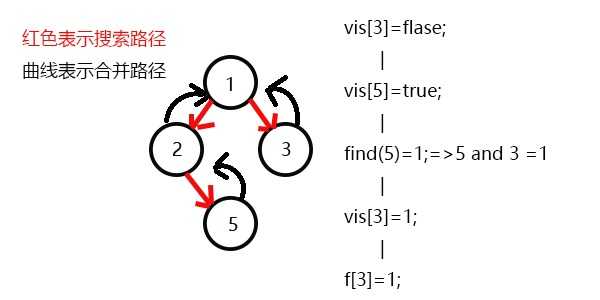
更新f[6]=3,发现3没有没被搜过的子节点了,则寻找与3有关系的点;
发现5和3有关系,此时vis[5]=1,则它们的最近公共祖先为find(5)=1;
(find(5)的顺序为f[5]=2-->f[2]=1-->f[1]=1 return 1;)
发现没有和3有关系的点了,返回此前一次搜索,更新vis[3]=1;
更新f[3]=1,发现1没有被搜过的子节点也没有有关系的点,此时可以退出整个dfs了。
本文内容摘抄于:
LCA_百度百科
最近公共祖先LCA(Tarjan算法)的思考和算法实现 - JVxie - 博客园
以上是关于LCA算法的主要内容,如果未能解决你的问题,请参考以下文章



