[2019 美团春招实习笔试] 2. 染色格子数量

Posted 2021-10-31 shiyublog

时间限制：C/C++语言 1000MS；其他语言 3000MS
内存限制：C/C++语言 65536KB；其他语言 589824KB
题目描述：
在二维平面上有一个无限的网格图形，初始状态下，所有的格子都是空白的。现在有n个操作，每个操作是选择一行或一列，并在这行或这列上选择两个端点网格，把以这两个网格为端点的区间内的所有网格染黑（包含这两个端点）。问经过n次操作之后，共有多少个格子被染黑，显然在众多操作中，很容易重复染色同一个格子，这个时候只计数一次。

输入
输入第一行包含一个正整数n（1<=n<=10000）.

接下来n行，每行四个整数，x1，y1，x2，y2，分别表示一个操作的两端格子坐标。（-10^9<=x1,y1,x2,y2<=10^9）,若x1=x2则是在一列上染色，若y1=y2，则是在一行上染色，保证每次操作是在一行或一列上染色。 

输出
输出仅包含一个正整数，表示被染色的格子的数量。

样例输入
3
1 2 3 2
2 5 2 3
1 4 3 4
样例输出
8

算法：

矩形面积并，扫描线+离散化+线段树

参考链接：https://www.jianshu.com/p/d70f6d346913

但是本题目与之不同，

1. 本题目中，数值为整数；poj1151中数值为浮点值；

2. 本题目中，每一个整数坐标表示一个格子，每个单位格子面积为1；poj1151中每个浮点坐标表示一个点，点的面积为0；

在算法实现上，有以下变动

1. 输入坐标的转换

在读入数据时，将格子坐标转成了点坐标，具体实现就是：

对于(x1, y1, x2, y2)的输入，其在坐标系中的端点坐标为：(x1 - 1, y1, x2, y2 - 1)；并以此新坐标作为line的输入。

其中flag为lines[i]的标记符号，covered + flag记录x轴坐标的覆盖次数：

1）flag = 1，表示这条线为底部的线，扫描这条线则进入矩形区域，该线段上的所有横坐标覆盖次数 + 1，

2）flag = -1, 表示这条线为顶部的线，扫描这条线则退出矩形区域，该线段上的所有横坐标覆盖次数将 -1，

2. 线段树的构造

在poj1151中，线段树的每个节点表示一段区间：节点[1, 5) 表示真实区间 [0, 4)等；

下面代码中，将左闭右开的区间表示，转换为左闭右闭的表示：节点[1, 4] 表示真实区间 [0, 3]等；

因而，poj1151中的叶子节点为 [l, r), 其中 r == l + 1; 而下面代码中的叶子节点为 [l, r], 其中 r == l；

3. 线段树cnt的计算

每个节点的cnt的值，为其孩子节点cnt的值的加和，

在poj1151中，对于叶子节点，若被覆盖，则其cnt的值为segTree[t].real_r - segTree[t].real_l，表示这个左闭右开的区间长度；

在下面代码中，由于每个叶子节点只表示坐标系中的一个点，若其被cover，则该节点的cnt  = 0.5。为什么设置为0.5呢？以本题目样例说明：

3
1 2 3 2
2 5 2 3
1 4 3 4

则转换后的各条扫描线分别为：

lines[1]: y = 1, [x1, x2] = [0, 3], flag = 1;

lines[2]: y = 2, [x1, x2] = [0, 3], flag = -1;

lines[3]: y = 2, [x1, x2] = [1, 2], flag = 1;

lines[4]: y = 3, [x1, x2] = [0, 3], flag = 1;

lines[5]: y = 4, [x1, x2] = [0, 3], flag = -1;

lines[6]: y = 5, [x1, x2] = [1, 2], flag = -1;

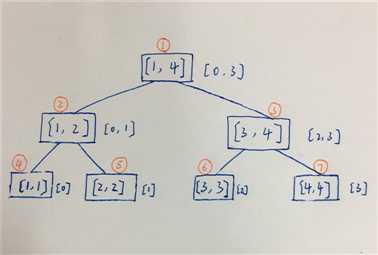
　　　　　　　　　　　　图1. 线段树

(图中矩形框中的[l ,r] 表示线段树节点的左右端点序号范围；每个矩形框右边的[real_l, real_r] 表示该节点对应的真实的左右端点x轴坐标范围。橙色标注的序号t表示线段树的第t个节点。)

对于lines[3], 该线段覆盖区域为[1, 2], 该区域长度为1；即上图中节点5, 6均被覆盖，则每个节点的cnt值应该设置为单位区间长度的一半，为0.5. 

代码：

  1 # include <bits/stdc++.h>
  2 using namespace std;
  3 
  4 const int maxn = 1e5;
  5 int n;
  6 set<int> x_set;
  7 set<int>::iterator it;
  8 int x[maxn * 2 + 10];
  9 
 10 struct TreeNode
 11 {
 12     int l, r;
 13     int real_l, real_r;
 14     int covered; // covered times
 15     double cnt; // total covered length in this zone
 16 }segTree[maxn * 2 + 10];
 17 
 18 struct Line
 19 {
 20     int y;
 21     int x1, x2;
 22     int flag;
 23 }lines[maxn * 2 + 10];
 24 
 25 bool cmp(Line a, Line b)
 26 {
 27     return a.y < b.y;
 28 }
 29 
 30 void build(int t, int l, int r)
 31 {
 32     segTree[t].l = l;
 33     segTree[t].r = r;
 34     segTree[t].real_l = x[l];
 35     segTree[t].real_r = x[r];
 36 
 37     segTree[t].covered = 0;
 38     segTree[t].cnt = 0;
 39 
 40     if(l == r) return;
 41     int mid = (l + r) >> 1;
 42     build(t << 1, l, mid);
 43     build(t << 1 | 1, mid + 1, r);
 44 }
 45 
 46 void calen(int t)
 47 {
 48     if(segTree[t].covered > 0)
 49     {
 50         double tmp = 0;
 51         if(segTree[t].l == segTree[t].r) tmp = 0.5;
 52         segTree[t].cnt = segTree[t].real_r - segTree[t].real_l + tmp;
 53         return;
 54     }
 55 
 56     if(segTree[t].r - segTree[t].l == 0) segTree[t].cnt = 0 ;
 57     else segTree[t].cnt = segTree[t << 1].cnt + segTree[t << 1 | 1].cnt;
 58 }
 59 
 60 void update(int t, Line line)
 61 {
 62     // line.x1 ~ line.x2 covered segTree[t].real_l ~ real_r => add 1
 63     if(segTree[t].real_l >= line.x1 && segTree[t].real_r <= line.x2)
 64     {
 65         segTree[t].covered += line.flag;
 66         calen(t);
 67         return;
 68     }
 69 
 70     // line not in the segTree[t] covered line
 71     if(segTree[t].real_l > line.x2 || segTree[t].real_r < line.x1) return;
 72 
 73     // update the child node
 74     update(t << 1, line);
 75     update(t << 1 | 1, line);
 76     calen(t); // 每个节点的cnt的值为其孩子节点cnt的值的加和, 更新完孩子节点cnt后要更新t节点cnt
 77 }
 78 
 79 
 80 int main()
 81 {   
 82     int x1, x2, y1, y2;
 83     while(cin >> n)
 84     {
 85         int t = 1;
 86         for(int i = 1; i <= n; ++i)
 87         {
 88             scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
 89             lines[t].y = y1;
 90             lines[t].x1 = x1 - 1;
 91             lines[t].x2 = x2;
 92             lines[t].flag = -1;
 93             x_set.insert(x1 - 1);
 94             ++t;
 95 
 96             lines[t].y = y2 - 1;
 97             lines[t].x1 = x1 - 1;
 98             lines[t].x2 = x2;
 99             lines[t].flag = 1; 
100             x_set.insert(x2);
101             ++t;           
102         }
103         sort(lines + 1, lines + t, cmp);
104 
105         int x_index = 1;
106         for(it = x_set.begin(); it != x_set.end(); ++it)
107         {
108             x[x_index++] = *it;
109         }
110         sort(x + 1, x + x_index);
111 
112         build(1, 1, x_index - 1);
113 
114         int res = 0;
115         update(1, lines[1]);
116         for(int i = 2; i < t; ++i)
117         {
118             int tmp = (lines[i].y - lines[i - 1].y) * segTree[1].cnt;
119             res += tmp;
120             update(1, lines[i]);
121         }
122 
123         cout << res << endl;
124     }
125     return 0;
126 }