竞赛中常见的数据结构
Posted 黑大帅之家
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了竞赛中常见的数据结构相关的知识,希望对你有一定的参考价值。
这篇文章结合15pku暑期training的资料,简单介绍几种竞赛中常见的数据结构,包括线段树、树状数组、伸展树、后缀数组、并查集等。
需要点明的这,这个专栏的文章可以视作一个“预处理”,是作为笔者16年暑期pku集训的一个先导,因此拘于时间和精力很多知识点都是从整体上把握,缺少细节缺少证明也缺少代码实现,这些东西笔者会在以后的训练中详细的介绍出来。
线段树:
对于细胞和人口的指数级爆炸我们都很熟悉,而在算法设计当中,最忌讳的也是出现O(2^n)的时间复杂度,我们将这个计算过程视为正向,那么我们反向行之,先进行排序然后每次筛掉一般,这也就是我们常说的”二分法“,我们能够发现,它与指数爆炸一样效率惊人,而线段树就是这样一个基于这种思想的数据结构。
为了满足每次能够“筛掉一半”,我们需要将要筛选的对象排序,最常见的就是在一个整数区间上进行建树,如下图。
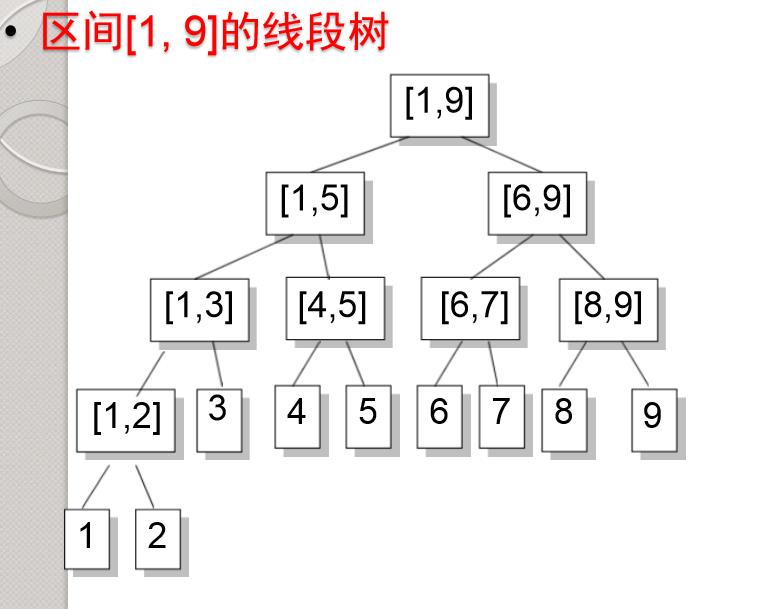
每个区间的长度是区间内整数的个数
叶子节点长度为1,不能再往下分
若一个节点对应的区间是[a,b],则其子节点对应的区间分 别是[a,(a+b)/2]和[ (a+b)/2+1,b] (除法去尾取整)
线段树的平分构造,实际上是用了二分的方法。若根节点对应的区间是[a,b],那么它的深度为log2 (b-a+1) +1 (向上取整)。
叶子节点的数目和根节点表示区间的长度相同.
由于它采取二分的搜索方式,树的深度一定不会超过log2 n + 1,n表示这个区间整数元素的个数,这使得我们访问这个区间上任何一个元素的时间复杂度都是O(log n)的,这相对于朴素的查找优化了太多,为我们在一个区间上进行查找、插入、更改和统计的优化提供了理论基础。
下面结合具体的问题来强化理解。
线段树:关于线段树主要是建树、查询、更新节点,稍微有些难度的是面临具体的离散处理。
Q1(Problem source : poj 3264):
Description
For the daily milking, Farmer John\'s N cows (1 ≤ N ≤ 50,000) always line up in the same order. One day Farmer John decides to organize a game of Ultimate Frisbee with some of the cows. To keep things simple, he will take a contiguous range of cows from the milking lineup to play the game. However, for all the cows to have fun they should not differ too much in height.
Farmer John has made a list of Q (1 ≤ Q ≤ 200,000) potential groups of cows and their heights (1 ≤ height ≤ 1,000,000). For each group, he wants your help to determine the difference in height between the shortest and the tallest cow in the group.
Input
#include<iostream> #include<cstdio> using namespace std; const int INF = 0xffffff0; int minV = INF; int maxV = -INF; struct Node //不要左右子节点指针的做法 { int L, R; int minV,maxV; int Mid() { return (L+R)/2; } }; Node tree[800010]; //4倍叶子节点的数量就够 void BuildTree(int root , int L, int R)//建立空树,这里根节点是从0开始的,因此对于根root的左右子节点是2*root + 1 , 2*root + 2. { tree[root].L = L; tree[root].R = R; tree[root].minV = INF; tree[root].maxV = - INF; if( L != R ) { BuildTree(2*root+1,L,(L+R)/2); BuildTree(2*root+2,(L+R)/2 + 1, R); } } void Insert(int root, int i,int v) //将第i个数,其值为v,插入线段树 { if( tree[root].L == tree[root].R ) { //成立则亦有 tree[root].R == i tree[root].minV = tree[root].maxV = v; return; } tree[root].minV = min(tree[root].minV,v); tree[root].maxV = max(tree[root].maxV,v); if( i <= tree[root].Mid() ) Insert(2*root+1,i,v); else Insert(2*root+2,i,v); } void Query(int root,int s,int e) { //查询区间[s,e]中的最小值和最大值,如果更优就记在全局变量里 //minV和maxV里 if( tree[root].minV >= minV && tree[root].maxV <= maxV ) //一个简直操作,用来优化已经找到[s,e]区间的最大值最小值之后还没有结束的二分搜索。 return; if( tree[root].L == s && tree[root].R == e ) { minV = min(minV,tree[root].minV); maxV = max(maxV,tree[root].maxV); return ; } if( e <= tree[root].Mid()) Query(2*root+1,s,e); else if( s > tree[root].Mid() ) Query(2*root+2,s,e); else { Query(2*root+1,s,tree[root].Mid()); Query(2*root+2,tree[root].Mid()+1,e); } } int main() { int n,q,h; int i,j,k; while(scanf("%d%d",&n,&q) != EOF) { BuildTree(0,1,n); for( i = 1;i <= n;i ++ ) { scanf("%d",&h); Insert(0,i,h); } for( i = 0;i < q;i ++ ) { int s,e; scanf("%d%d", &s,&e); minV = INF; maxV = -INF; Query(0,s,e); printf("%d\\n",maxV - minV); } } return 0; }
基于线段树查询线性序列的区间和(hdu 1166):
基于原始的线段树模板稍微改动一下即可,这里表面上有两个操作:ADD和SUB,但是它是基于点的更新,因此它本质上还是Insert函数。
简单的参考代码如下(时间原因,格式未改,还没有提交)。
#include<iostream> #include<cstdio> using namespace std; const int INF = 0xffffff0; long long temp; struct Node //不要左右子节点指针的做法 { int L, R; long long sum; int Mid() { return (L+R)/2; } }; Node tree[800010]; //4倍叶子节点的数量就够 void BuildTree(int root , int L, int R)//建立空树,这里根节点是从0开始的,因此对于根root的左右子节点是2*root + 1 , 2*root + 2. { tree[root].L = L; tree[root].R = R; tree[root].sum = 0; if( L != R ) { BuildTree(2*root+1,L,(L+R)/2); BuildTree(2*root+2,(L+R)/2 + 1, R); } } void Insert(int root, int i,int v) //将第i个数,其值为v,插入线段树 { if( tree[root].L == tree[root].R ) { //成立则亦有 tree[root].R == i tree[root].sum = v; return; } tree[root].sum += v; if( i <= tree[root].Mid() ) Insert(2*root+1,i,v); else Insert(2*root+2,i,v); } void Query(int root,int s,int e) { //查询区间[s,e]中的最小值和最大值,如果更优就记在全局变量里 //minV和maxV里 if( tree[root].L == s && tree[root].R == e ) { temp = tree[root].sum; return ; } if( e <= tree[root].Mid()) Query(2*root+1,s,e); else if( s > tree[root].Mid() ) Query(2*root+2,s,e); else { Query(2*root+1,s,tree[root].Mid()); Query(2*root+2,tree[root].Mid()+1,e); } } int main() { int n,t,h,q; int i,j,k; char str[10]; while(scanf("%d%d",&t,&n) != EOF) { BuildTree(0,1,n); for( i = 1;i <= n;i ++ ) { scanf("%d",&h); Insert(0,i,h); } while(1) { cin>>str; if(str[0] == \'A\'){ scanf("%d %d",&i,&j); Insert(0,i,j); } else if(str[0] == \'S\'){ scanf("%d %d",&i,&j); Insert(0,i,-j); } else{ int s , e; scanf("%d%d", &s,&e); Query(0,s,e); printf("%lld\\n",temp); } } } return 0; }
关于线段树的区间更新(pku 3468):
对比上面的题目,这里是基于一个线性表,每次更新区间上所有元素的数值,在原有点更新(log n)的基础上,如果这里按照朴素的做法,将区间更新变成点更新,那么点更新的时间复杂度是n log n,这里有一种方法能够降低时间复杂度。
其做法就是,建树过程中每个节点增加一个参量lnc,在区间更新操作的时候,遍历线段树,待更新区间完全覆盖当前区间时,更新当前节点的lnc值,不再继续向下遍历。因此在进行区间查询操作的时候,出现如下的两种情况:
(1)待查询区间完全覆盖当前节点所表述区间,因此结果只需要在当前节点记录的原有的区间和的基础上,加上当前节点的lnc*(区间长度)即可。
(2)如果带查询区间只是覆盖当前节点所表述区间的一部分,那么,这里我们将当前节点的lnc值往下拖,给它的两个子节点,然后清除当前节点的lnc值。可以看到,这样做的结果必然会导致出现(1)情况。
能够看到,这样做实现了信息的高效利用,避免了一些信息量少但是却浪费了时间复杂度的情况。
简单的参考代码如下。
#include <iostream> using namespace std; struct CNode { int L ,R; CNode * pLeft, * pRight; long long nSum; //原来的和 long long Inc; //增量c的累加 }; CNode Tree[200010]; // 2倍叶子节点数目就够 int nCount = 0; int Mid( CNode * pRoot) { return (pRoot->L + pRoot->R)/2; } void BuildTree(CNode * pRoot,int L, int R) { pRoot->L = L; pRoot->R = R; pRoot->nSum = 0; pRoot->Inc = 0; if( L == R) return; nCount ++; pRoot->pLeft = Tree + nCount; nCount ++; pRoot->pRight = Tree + nCount; BuildTree(pRoot->pLeft,L,(L+R)/2); BuildTree(pRoot->pRight,(L+R)/2+1,R); } void Insert( CNode * pRoot,int i, int v) { if( pRoot->L == i && pRoot->R == i) { pRoot->nSum = v; return ; } pRoot->nSum += v; if( i <= Mid(pRoot)) Insert(pRoot->pLeft,i,v); else Insert(pRoot->pRight,i,v); } void Add( CNode * pRoot, int a, int b, long long c) { if( pRoot->L == a && pRoot->R == b) {pRoot->Inc += c; return ;} pRoot->nSum += c * ( b - a + 1) ; if( b <= (pRoot->L + pRoot->R)/2) Add(pRoot->pLeft,a,b,c); else if( a >= (pRoot->L + pRoot->R)/2 +1) Add(pRoot->pRight,a,b,c); else { Add(pRoot->pLeft,a, (pRoot->L + pRoot->R)/2 ,c); Add(pRoot->pRight, (pRoot->L + pRoot->R)/2 + 1,b,c); } } long long QuerynSum( CNode * pRoot, int a, int b) { if( pRoot->L == a && pRoot->R == b) return pRoot->nSum + (pRoot->R - pRoot->L + 1) * pRoot->Inc ; pRoot->nSum += (pRoot->R - pRoot->L + 1) * pRoot->Inc ; Add( pRoot->pLeft,pRoot->L,Mid(pRoot),pRoot->Inc); Add( pRoot->pRight,Mid(pRoot) + 1,pRoot->R,pRoot->Inc); pRoot->Inc = 0; if( b <= Mid(pRoot)) return QuerynSum(pRoot->pLeft,a,b); else if( a >= Mid(pRoot) + 1) return QuerynSum(pRoot->pRight,a,b); else return QuerynSum(pRoot->pLeft,a,Mid(pRoot)) + QuerynSum(pRoot->pRight,Mid(pRoot) + 1,b); } int main() { int n,q,a,b,c; char cmd[10]; scanf("%d%d",&n,&q); int i,j,k; nCount = 0; BuildTree(Tree,1,n); for( i = 1;i <= n;i ++ ) { scanf("%d",&a); Insert(Tree,i,a);} for( i = 0;i < q;i ++ ) { scanf("%s",cmd); if ( cmd[0] == \'C\' ) {scanf("%d%d%d",&a,&b,&c); Add( Tree,a,b,c); } else {scanf("%d%d",&a,&b); printf("%I64d\\n",QuerynSum(Tree,a,b));} } return 0; }
关于并查集:
Q1(Problem source : poj 1611):
Description
Input
Output
#include<cstdio> using namespace std; const int maxn = 30000 + 5; int total[maxn];//记录某节点为根并查集的元素个数 int parent[maxn]; int Find(int a) { if(parent[a] == a) return a; else return parent[a] = Find(parent[a]);//状态压缩 } void Merge(int x , int y) { int p1 = Find(x); int p2 = Find(y); if(p1 == p2) return; else { parent[p2] = p1; total[p1] += total[p2]; } } int main() { int n , m , k; int a , b; while(scanf("%d%d",&n,&m) != EOF) { if( n == 0 && m == 0) break; for(int i = 0;i < n;i++) {parent[i] = i ; total[i] = 1;} for(int i = 0;i < m;i++) { scanf("%d",&k); scanf("%d",&a); for(int i = 1;i <k;i++) { scanf("%d",&b); Merge(a , b); } } printf("%d\\n",total[Find(0)]); } }
Q2(2016-百练-ACM暑期课练习题(二)-07):
描述
输入:输入包括多组数据。 每组数据的第一行包括n和m,0 <= m <= n(n-1)/2,其后m行每行包括两个数字i和j,表示学生i和学生j信仰同一宗教,学生被标号为1至n。输入以一行 n = m = 0 作为结束。
输出:对于每组数据,先输出它的编号(从1开始),接着输出学生信仰的不同宗教的数目上限。
分析:很裸的并查集求不相交集合的数量的题目,在上题代码的基础上,最后扫一遍记录父节点的parent[]数组完成计数。简单的参考代码如下:
#include<cstdio> using namespace std; const int maxn = 50000 + 5; int parent[maxn]; int Find(int a) { if(parent[a] == a) return a; else return parent[a] = Find(parent[a]);//状态压缩 } void Merge(int x , int y) { int p1 = Find(x); int p2 = Find(y); if(p1 == p2) return; else { parent[p2] = p1; } } int main() { int n , m ; int a , b; int tt = 1; while(scanf("%d%d",&n,&m) != EOF) { if( n == 0 && m == 0) break; for(int i = 1;i <= n;i++) {parent[i] = i ;} for(int i = 0;i < m;i++) { scanf("%d%d",&a,&b); Merge(a , b); } int cnt = 0; for(int i = 1;i <= n;i++) { if(parent[i] == i) cnt++; } printf("Case %d: %d\\n",tt++,cnt); } }
关于字典树(Problem source:hdu1251)
所谓字典树就是在朴素的二维数组储存大量字符串的基础上,进行的数据结构优化,它最大的一个特点就是节省空间(当然进行查找操作的时候也会节省时间),因为在字典树中,有相同前缀的字符串只开辟一次空间。
下面拿一个例题来呈现以下字典树建树和查找的过程(涉及类链表的算法设计,理解指针怎么操作这个算法就很简单)。
#include<iostream> #include<cstdio> #include<cstring> using namespace std; struct node { int cnt; struct node *next[26]; node() { cnt=0; memset(next,0,sizeof(next)); } }; node *root=NULL; void buildtrie(char *s) { node *p=root; node *tmp=NULL; int i,l=strlen(s); for(i=0;i<l;i++) { if(p->next[s[i]-\'a\']==NULL) { tmp=new node; p->next[s[i]-\'a\']=tmp; } p=p->next[s[i]-\'a\']; p->cnt++; } } void findtrie(char *s) { node *p=root; int i,l=strlen(s); for(i=0;i<l;i++) { if(p->next[s[i]-\'a\']==NULL) { printf("0\\n"); return; } p=p->next[s[i]-\'a\']; } printf("%d\\n",p->cnt); } int main() { char str[11]; root=new node; while(gets(str)) { if(strcmp(str,"")==0) break; buildtrie(str); } while(scanf("%s",str)!=EOF) { findtrie(str); } return 0; }
关于字典树的补充(Problem source : hdu 5687)
在字典树中常见的操作除了上文给出的建树和查找,还有删除。
#include <iostream> #include <cstdio> #include <cstring> #include <cstdlib> using namespace std; const int maxn = 30; struct Trie{ int cnt; Trie *next[maxn]; Trie(){ cnt = 0; memset(next,0,sizeof(next)); } }; Trie *root; void Insert(char *word) { Trie *tem = root; while(*word != \'\\0\') { int x = *word - \'a\'; if(tem->next[x] == NULL) tem->next[x] = new Trie; tem = tem->next[x]; tem->cnt++; word++; } } int Search(char *word) { Trie *tem = root; for(int i=0;word[i]!=\'\\0\';i++) { int x = word[i]-\'a\'; if(tem->next[x] == NULL) return 0; tem = tem->next[x]; } return tem->cnt; } void Delete(char *word,int t) { Trie *tem = root; for(int i=0;word[i]!=\'\\0\';i++) { int x = word[i]-\'a\'; tem = tem->next[x]; (tem->cnt)-=t; } for(int i=0;i<maxn;i++) tem->next[i] = NULL; } int main() { int n; char str1[50]; char str2[50]; while(scanf("%d",&n)!=EOF) { root = new Trie; while(n--) { scanf("%s %s",str1,str2); if(str1[