决策树的剪枝

Posted 2021-10-22 keye

决策树算法原理(ID3，C4.5)

决策树算法原理(CART分类树)

CART回归树

 

　　决策树的剪枝是通过极小化决策树整体的损失函数。(决策树的生成只考虑局部最优，决策树的剪枝考虑全局最优)

　　设树T的叶节点为 t，个数为 |T|，该叶节点有 N_t 个样本点，其中 k 类的样本点有 N_tk 个，k = 1,2,...,K，H_t(T)为叶节点 t 上的经验熵，α≥0为参数，则决策树的损失函数：

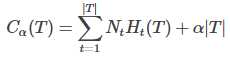
其中经验熵H_t(T)，也称特征熵：

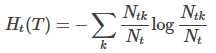
在损失函数中，式子右端的第一项记作：

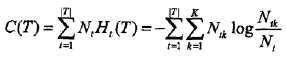
这时损失函数为：

C_α(T) = C(T) + α|T|

C(T) 表示模型对训练数据的预测误差，即模型与训练数据拟合程度，|T| 表示模型复杂度，参数 α≥0控制两者之间的影响。较大的α促使选择简单的模型（树），较小的α促使选择复杂的模型（树），α=0只考虑模型与训练数据的拟合程度，不考虑模型的复杂度。

　　当α确定时，子树越大，与训练数据拟合越好，但模型复杂度越高；相反，子树越小，与训练数据拟合不好，但模型复杂度低。

　　上面两个决策树损失函数的极小化等价于正则化的极大似然估计。所以，利用损失函数最小原则进行剪枝就是用正则化的极大似然估计进行模型选择。